Определение возможностьи применения железобетонных шпал типа 2Ш27-Ат800СБ при обращении четырехосных грузовых вагонов с повышенными осевыми нагрузками до 230 кН со скоростью 80 км/час в кривых, страница 2

A_z=0,6245,                        A_z-ά=0,9479,                     A_z-β=0,9942

B_z=1,1344,                         B_z-ά=0,7400,                      B_z-β=0,4318

C_z=0,7336,                         C_z-ά=0,2786,                      C_z-β=0,0934

D_z=,0,3044                         D_z-ά=0,06958,                     D_z-β=0,01346

Силовые и геометрические характеристики в любой точке подрельсового сечения шпалы определяются следующими уравнениями:

На участке от точки b до О₂ , а именно в точке О₂:

;

;

;

.

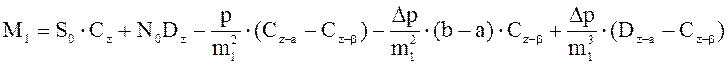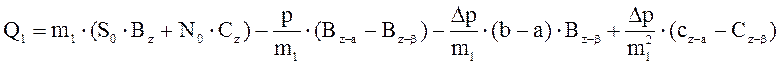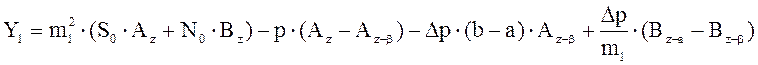После подстановки значений и приведения подобных получим:

;

;

;

.

На втором, среднем, участке шпалы: b₂=0,240 м; I_red2=7,672∙10^-5 м^-4.

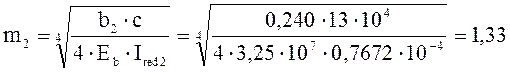 м^-1.

Для середины шпалы: λ=m₂∙l₂=1,33∙0,3=0,399. Для этого аргумента находим значения функций:

А_λ=0,9958;     B_λ=0,3986;    C_λ=0,0796;      D_λ=0,0106;    ψ=b₂/b₁=0,240/0,270=0,889

Для середины шпалы Q_λ=0 и Ф_λ=0.

 ;

 .

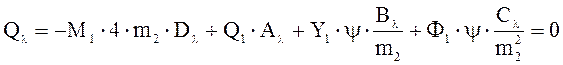Подставив в эти уравнения выражения для М₁, Q₁, Y₁, Ф₁ и решив эти уравнения относительно S₀ и N₀, получим:

S₀=66,116

N₀= -16,301

Определим значения изгибающих моментов, поперечных сил и прогибов (давлений на балласт) в наиболее характерных точках шпалы.

Конец шпалы М=0, Q=0:

Прогиб в 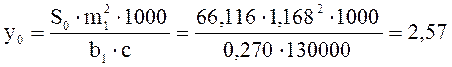мм:

 мм.

Учитывая размерность величин находим давление на балласт под концом шпалы:

кПа.

Сечение по середине подрельсовой площадки шпалы:

ρ=m1∙r=1,168∙0,545=0,637 ρ-α=0,158.

Для этих аргументов находим значения функций:

A_ρ=0,9726;     C_ρ=0,2024;     A_ρ-α=0,9999;        C_ρ-α=0,0124;

B_ρ=0,6333;     D_ρ=0,0430;    B_ρ-α=0,1577;         D_ρ-α=0,6540.

Момент посередине подрельсовой площадки шпалы:

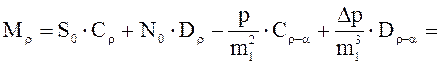
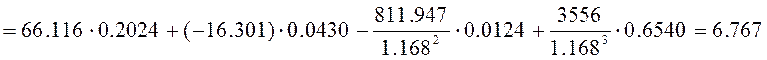 кН∙м;

Поперечная сила посередине подрельсовой площадки:

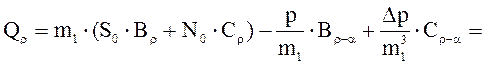
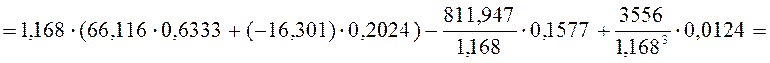
 кН

Прогиб посередине подрельсовой площадки:

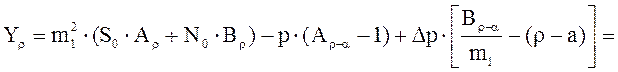
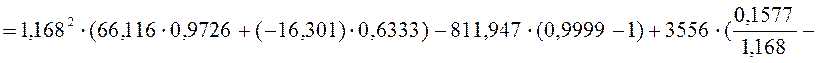
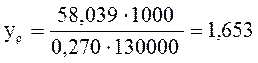 мм

Давление на балласт:

 кПа.

Переходное сечение от первого участка ко второму:

Подставляя в приведенные выше уравнения для М₁, Q₁, Y₁ значения S₀ и N₀, получим:

М₁=-7.19 кН∙м; Q₁=-12,91 кН; Y₁=52,086;

Прогиб:

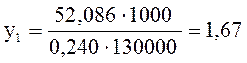 мм.

Давление на балласт:

 кПа.

Сечение по середине шпалы:

Момент в сечении:

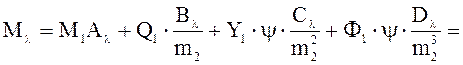
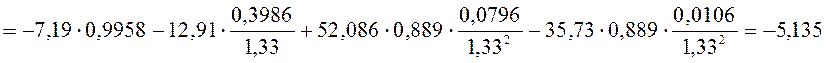 кН∙м.

3.3. Расчет выносливости и трещинностойкости шпалы.

Расчетные характеристики материалов

Бетон тяжелый, проектного класса по прочности на сжатие В40, по морозостойкости F200.

R_bn=29,0 МПа, R_b=R_bn/γ_bc=29,0/1,3=22,308 МПа;

R_btn=2,1 МПа, R_bt=R_btn/γ_bt=2,1/1,5=1,4 МПа;

E_b=32,5∙10³ МПа;

Арматура - напрягаемая термически упрочненная диаметром 12 мм класса прочности Ат800 (Ат-V).

A_sp=4,5239∙10^-4 м²; R_sn=785 МПа; R_s=R_sn/γ_s=680 МПа; E_s=19∙10⁴ МПа.

α=E_s/E_b=19∙10⁴/32,5∙10³=5,846; при расчете выносливости α’=10.

Геометрические характеристики расчетного сечения по середине подрельсовой площадки:

Площадь напрягаемой арматуры:

A_sp=4,524∙10^-4 м²;

Расстояние от нижней грани до центра тяжести арматуры:

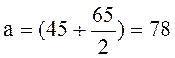 мм;

Площадь сечения:

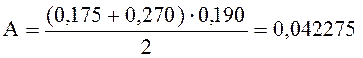 м²;

Приведенная площадь сечения:

м²;

Статический момент бетонного сечения:

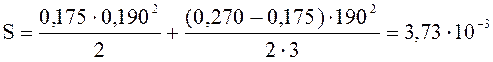м³;

Приведенный статический момент сечения:

м³;

Центр тяжести приведенного сечения:

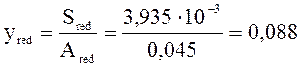 м;

Эксцентриситет усилия предварительного обжатия:

 м;

Момент инерции сечения:

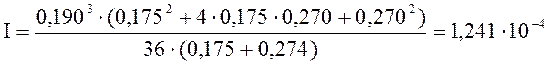 м⁴;

Момент инерции приведенного сечения;

 м⁴.

Те же характеристики при α’=10:

 м²;

 м³;

 м;

м;

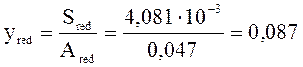 м⁴;

Ширина сечения шпалы на уровне центра тяжести приведенного сечения:

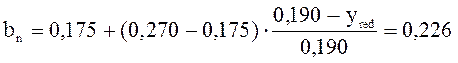 м;

Статический момент половины бетонного сечения:

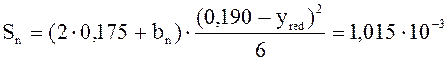 м³;

Статический момент половины приведенного сечения:

м³.

Предварительное натяжение арматуры и его потери

В проекте шпалы принято σ_sp=570 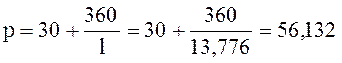МПа;

 МПа;

σ_sp+p=626,132 МПа  <  R_s,ser=785 МПа;

σ_sp-p=513,868 МПа  >  0,3∙_Rs,ser=235,5 МПа.

Таким образом, величина σ_sp находится в допускаемых по СНиП 2.03.01-84 пределах.

Патери напряжения общие для всех сечений шпалы:

Первые потери (I).

1. Релаксация напряжений арматуры

σ₁=0,03∙σ_sp=0,03∙570=17,1 МПа.

2. Температурный перепад (разность температур натянутой арматуры в зоне нагрева и поддона воспринимающего усилие натяжения при прогреве бетона)

Δt=65 ºC,    σ₂=1,25∙Δt=1,25∙65=81,25 МПа.

3. Деформация анкеров, расположенных у натяжных устройств

При электротермическом способе натяжения потери от деформаций анкеров в расчете не учитываются, так как они учтены при определении значения полного удлинения арматуры, следовательно σ₃=0.

4. Трение арматуры

σ₄=0.

5. Деформация стальной формы при изготовлении предварительно напряженных конструкций

При электротермическом способе натяжения потери от деформации формы в расчете не учитываются, так как они учтены при определении значения полного удлинения арматуры, следовательно σ₅=0.