Лекция 4
Динамические характеристики непрерывных линейных стационарных систем.
Линеаризация. Требования, предъявляемые к системе
План
1. Временные характеристики непрерывных линейных стационарных систем
2. Частотные характеристики непрерывных линейных стационарных систем
3. Линеаризация
4. Требования, предъявляемые к системе
Качество любой автоматической системы можно оценить в числе только с использованием специальных характеристик.
Все характеристики систем управления делятся на два больших класса – статические и динамические. Статические характеристики позволяют судить о качестве системы в устойчивых состояниях, когда все внешние сигналы и все сигналы внутри системы постоянны. Обычно такие характеристики показывают связь одной величины в системе с другой. Динамические характеристики дают представление о поведении системы во времени, о переходных процессах, происходящих в ней. Именно поэтому в теории управления по преимуществу исследуются динамические характеристики систем.
Начнем изучение динамических характеристик непрерывных стационарных линейных систем управления с большого класса временных характеристик. Если вспомнить типовые воздействия, описанные в предыдущей лекции, то основными из них следует назвать единичную ступенчатую и единичную импульсную функции. Пусть u(t) – входное воздействие и х(t) – выходной сигнал системы (рис.1)

Тогда, подавая единичную ступенчатую функцию в качестве входного воздействия u(t)=1(t), получим x(t)=h(t) , где h(t) – переходная характеристика системы (рис.2).
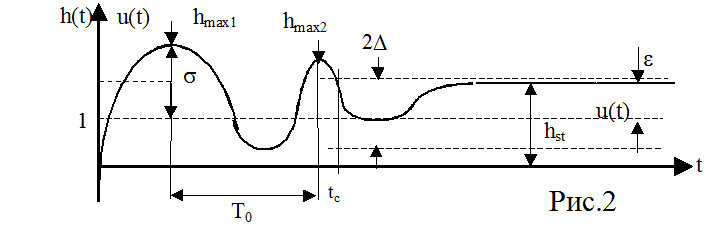
Переходная характеристика имеет следующие основные параметры
1. Время регулирования (tc) – время, за которое регулируемая величина достигает заданного значения с заданной точностью D,%;
2. Перерегулирование - (s,%)
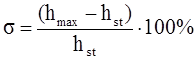
Эта величина очень важна при регулировании, так как большое перерегулирование может нарушать нормальное функционирование системы.
3. Период колебаний (T0);
4.
Коэффициент затухания 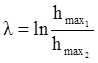 .
.
Период колебаний и коэффициент затухания можно определить только для систем с колебательным характером переходного процесса. Если переходный процесс имеет апериодических характер (рис.3), то можно найти только время регулирования
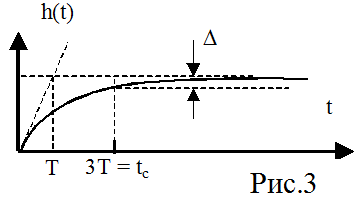
Но для этого типа переходного процесса можно найти другой параметр - T – постоянную времени. Для линейных систем предполагают, что постоянная времени отсекается на горизонтальной прямой., проведенной на уровне установившегося значения выходной величины, прямой , проведенной с начальным наклоном переходной характеристики. В соответствии с этим для линейных систем время регулирования обычно определяется как tc=3T. В течение этого времени переходная характеристика входит в зону точности 10% (рис.3).
Аналогично переходной характеристике вводится импульсная переходная характеристика (весовая функция), которая является реакцией системы на единичную импульсную функцию (d-функцию) (рис.4).

В соответствии с видом весовой функции все системы можно разделить на два класса – статические и астатические. Весовая функция статической системы удовлетворяет условию:
![]()
(см. рис. 4). Для астатических систем
![]()
(A= const ¹0). Переходная характеристика астатических систем не имеет установившегося положения. Площадь под кривой весовой характеристики показывает степень демпфирования системы: чем больше площадь, тем хуже система задемпфирован.
Другой большой класс динамических характеристик систем управления – это частотные характеристики. Частотные характеристики показывают результат воздействия на вход системы гармонического сигнала. Для систем регулирования прежде всего рассматривают две частотные характеристики – амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.