Динамические характеристики непрерывных линейных стационарных систем. Линеаризация. Требования, предъявляемые к системе, страница 2

Амплитудно-частотная характеристика является функцией, связывающей амплитуду выходного (гармонического) сигнала системы с частотой этого воздействия (рис.5). Она показывает, во сколько раз увеличится (уменьшится) амплитуда синусоиды, прошедшей через систему.

Фазочастотная характеристика таким же образом связывает  фазовое запаздывание на выходе с частотой синусоиды проходящей через систему. (рис.6).

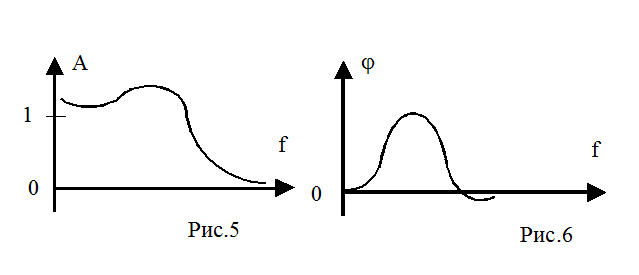
Частотные характеристики очень важны при изучении свойств систем управления, так как они показывают возможность системы передавать (воспроизводить, отрабатывать) сигналы с различными частотами, то есть показывают, как работает система в разных режимах

Довольно часто для представления частотных характеристик применяют логарифмическую шкалу, в которой по оси абсцисс откладывают величину  lgω. (w=2pf – круговая частота ). Изменение w в 10 раз дает единицу по этой оси, которая называется декадой (dec).

По оси ординат АЧХ измеряется в децибелах (dB). Эта мера пропорциональна величине

20lgK,

где 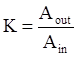- коэффициент усиления  (отношение амплитуды выходного гармонического сигнала к амплитуде входного). Таким образом, логарифмическая АЧХ (ЛАЧХ) получается из  АЧХ в линейном масштабе путем следующего преобразования:

L(w)=20lg|W(j w)|=20lgA(w). [dB].

Отрицательные значения  L(w) соответствуют  уменьшению амплитуды сигнала системой.

Логарифмическая фазочастотная характеристика  (ЛФЧХ) отличается от обычной фазочастотной только логарифмическим масштабом частот.

Особенно важной чертой ЛАЧХ является то, что в логарифмическом масштабе АЧХ линейной системы может быть представлена в виде  линейных асимптот, к которым довольно хорошо приближается реальная зависимость. Для ЛФЧХ каждая кривая, будучи смещенной вдоль оси частот, будет представлять множество других ФЧХ для систем с подобной структурой, но другими параметрами.

Вид ЛАЧХ и ЛФЧХ некоторой системы представлен на рис.7.

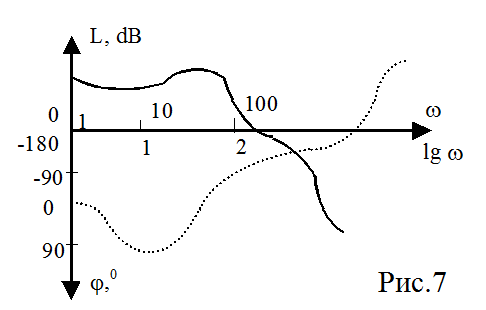
Другой формой частотных характеристик систем управления является комплексная амплитудно-фазовая ЧХ. Она имеет вид годографа: модуль описывающего вектора соответствует величине амплитудной характеристики на данной частоте, а аргумент (угол поворота) соответствует ФЧХ (рис.8)

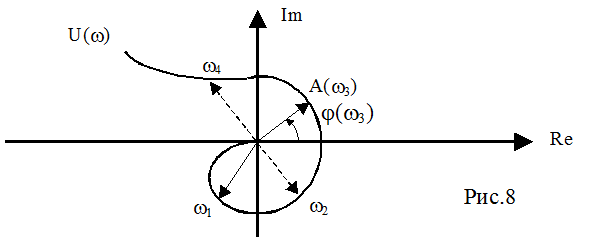
Иногда этот годограф представляют в виде совокупности двух характеристик P(w)=Re[U(w)]  - (действительной АФЧХ) и  Q(w)=Im[U(w)] (мнимой АФЧХ).

Все рассмотренные нами характеристики применяются преимущественно для линейных стационарных систем, так как  только в этом классе систем характеристики постоянны для любого конечного значения амплитуды входного гармонического сигнала. (Выходная амплитуда будет здесь строго пропорциональна входному сигналу).

Линейная теория очень удобна для инженерных расчетов, но большинство реальных систем управления являются нелинейными. Для решения этой проблемы часто применяют процедуру линеаризации. Основным принципом, лежащим в основе метода линеаризации является замена нелинейной статической характеристики того или иного элемента некоторым постоянным коэффициентом линеаризации (K_l). Наиболее простой путь для того, чтобы линеаризовать зависимость y = f(x) – это заменить ее в точке линеаризации х₀ первой производной (рис.9):

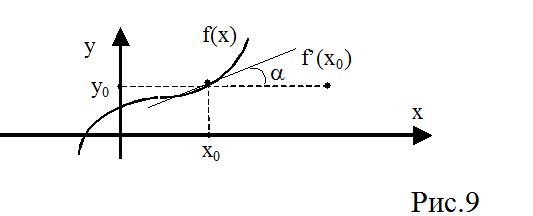
Такая линеаризация называется линеаризацией по касательной. Этот метод хорошо работает для малых отклонений от точки линеаризации. В других случаях применяют линеаризацию по секущей или даже заменяют нелинейную зависимость переменным по времени коэффициентом линеаризации.

Требования, предъявляемые к системе, обычно определяются параметрами динамических характеристик (частотных и временных). Наиболее часто ограничения накладывают на время регулирования, перерегулирование, фазовое запаздывание в некотоpом диапазоне частот, минимальное или максимальное значение АЧХ в некотоpом диапазоне частот. Для точности систем преимущественное значение имеет величина установившейся ошибки.