Проверка прочности корпуса судна, страница 11

№ пластины	Редукционный коэффициент		Площадь	Потеря площади	Расстояние от условной оси	Потеря статического момента	Потеря момент инерции
							переносного	собственного
1	2	3	4	5	6	7	8	9
1	1	0	312	0	0,792	0	0	0
2	1	0	65,4	0	0,792	0	0	0
3	0,07	0,93	170,4	158,472	2,366	374,945	887,12	0
4	0,07	0,93	191,4	178,002	3,973	707,202	2809,714	0
5	0,01	0,99	65,4	64,746	4,844	313,63	1519,224	0
6	0,03	0,97	93,6	90,792	4,844	439,796	2130,372	0
7	0,07	0,93	89,52	83,254	1,173	97,657	114,552	0
8	1	0	896	0	0	0	0	0
Итого				= 575,266		= 1933,23	= 7460,982

            Площадь половины ЭБ в третьем приближении , ее статический момент , определили по выражениям:

;

.

Отстояние нейтральной оси от основной плоскости во втором приближении определили по формуле:

.

МИЭБ относительно нейтральной оси во втором приближении  нашли по формуле:

.

Для нахождения наибольших нормальных напряжений во втором приближении вычислили сопротивления эквивалентного бруса (МСЭБ) для днищевых и палубных поясков.

 ;

,

;

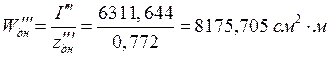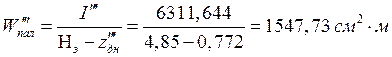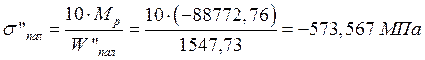
  Напряжения третьего приближения отличаются менее, чем на 5% .

Сравниваем окончательные значения напряжений общего изгиба с допускаемыми напряжениями .

Найденные напряжения находятся в пределах допускаемых напряжений, что говорит о достаточной общей прочности судна.

4 Проверка местной прочности

     4.1 Схема расчета днищевого продольного ребра

На опоре в свободной кромке  (сжатие);

На опоре в присоединенном пояске обшивки  (растяжение);

В пролете в свободной кромке  (растяжение);

В пролете в присоединенном пояске обшивки  (сжатие).

 

1)  1)  Схема конструкции заменяется схемой балки

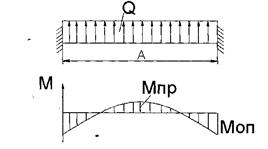
  t=0.8

	F,см2	Z,см	f·z,см2м	f·z2,см4	I,см4
Ребро жесткости 125х80х8	19,7	8,76	172,572	1511,73	312
Присоединенный поясок 0,8х11	8,8	0,4	3,52	1,408	0,469
Σ	28,5	-	176,092	1825,607

;

;

 

;

 ;

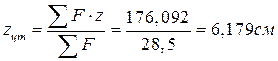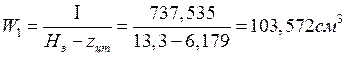
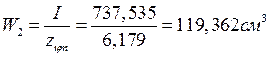=1,5м, b=0,5м;

2)  2)  Расчет нагрузки на продольное ребро,

3)  3)  Наибольший момент на опоре,

 

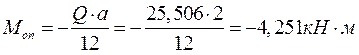
  4) Наибольший момент в пролете, 

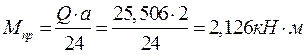
5) Определили напряжение по формуле:

                                          ;

;

;

;

.

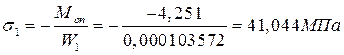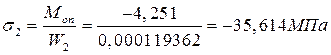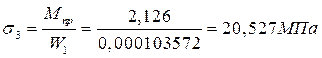6) Сравнили с допускаемыми значениями: в пролете []=0,85·_т=0,85·240=204МПа; на опоре []=0,95·_т=0,95·240=228МПа.

 Т.к. давление воды получилось меньше напряжения допускаемого, то давление местной прочности выполняется [] > .

4.2 Расчет балки полоски

Дано: a=2,0 м; b=0,5 м; t=0,8 см; h=2,6 м.

Так как a/b=2,0/0,5=4, то расчет пластины сводится к расчету БП шириной 1 см.

Нагрузка на БП:    

Соседние пластины находятся под таким же давлением воды, поэтому полагаем концы БП жестко заделанными.

 

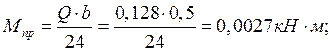
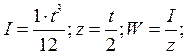
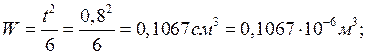
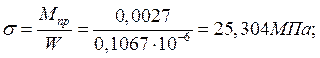
Так как > , то условие прочности выполняется.

4.3 Расчет прочности бортовой ветви холостого шпангоута

 Определили нагрузки, действующие на балку.

 

 

 

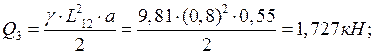
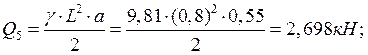
Нашли опорные моменты методом 3-х моментов.

 

Опора 1:

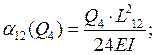
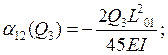
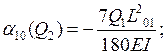
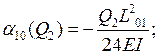
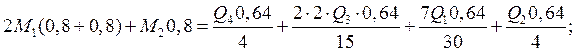
Опора 2:

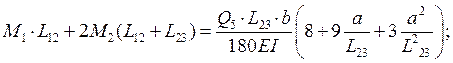
b=1м; a=0,6м; L₂₃=1,6м.

 

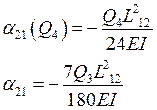
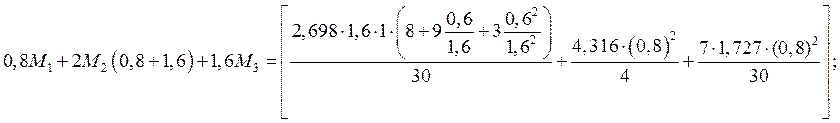
Опора 3:

 

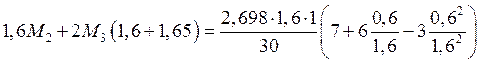
Решим систему:

5 Проверка прочности связей корпуса

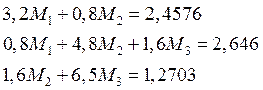
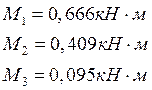
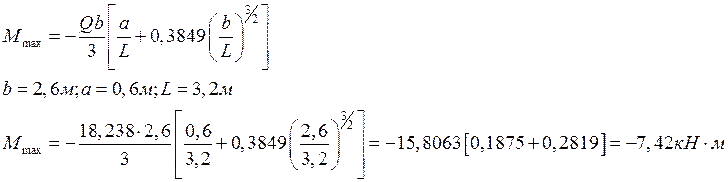
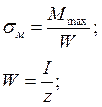
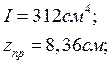
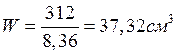
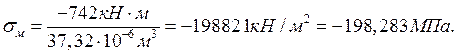
Связи могут участвовать в обеспечении: местной прочности; общей прочности; одновременно местной и общей прочности.