Цель работы
Экспериментально и теоретически исследовать резонансные явления в параллельном колебательном контуре.
4.1. Основные теоретические сведения
 Резонансом
в электрической цепи или на участке, содержащей индуктивности и ёмкости,
называют явление, при котором гармонические напряжение и ток на входе цепи
совпадают по фазе. Различают два вида резонанса: резонанс напряжений в
цепи, состоящей из последовательно соединённых индуктивности и ёмкости; и резонанс
токов в цепи с параллельным соединением двух ветвей, одна из них содержит
резистор и катушку индуктивности, вторая - резистор и конденсатор. Цепь, в
которой наблюдается резонанс напряжений, называется последовательным колебательным
контуром, а резонанс токов - параллельным колебательным контуром.
Резонансом
в электрической цепи или на участке, содержащей индуктивности и ёмкости,
называют явление, при котором гармонические напряжение и ток на входе цепи
совпадают по фазе. Различают два вида резонанса: резонанс напряжений в
цепи, состоящей из последовательно соединённых индуктивности и ёмкости; и резонанс
токов в цепи с параллельным соединением двух ветвей, одна из них содержит
резистор и катушку индуктивности, вторая - резистор и конденсатор. Цепь, в
которой наблюдается резонанс напряжений, называется последовательным колебательным
контуром, а резонанс токов - параллельным колебательным контуром.
а б
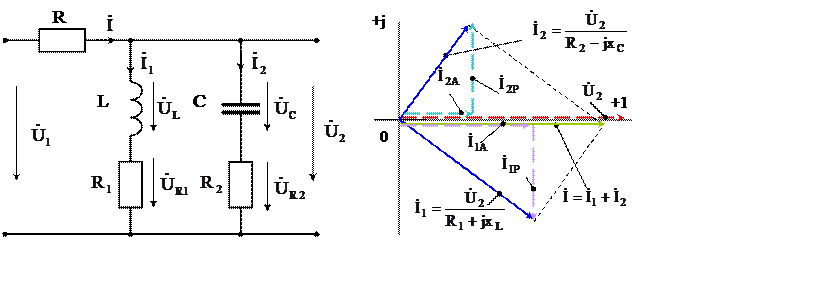
На рис. 4.1,а приведена схема параллельного
колебательного контура. Резонансные явления в параллельном колебательном
контуре называют резонансом токов. При резонансе реактивные составляющие токов
в индуктивности - ![]() и ёмкости -
и ёмкости - ![]() компенсируют друг друга (рис.
4.1,б).
компенсируют друг друга (рис.
4.1,б).
В режиме резонанса ток - ![]() и напряжение -
и напряжение - ![]() на
входе контура совпадают по фазе. Определим токи в ветвях
на
входе контура совпадают по фазе. Определим токи в ветвях
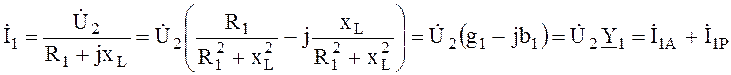 ; (4.1)
; (4.1)
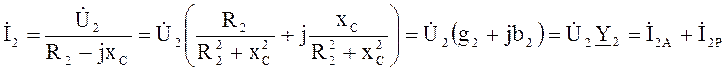 ; (4.2)
; (4.2)
![]() ;
;
![]() , (4.3)
, (4.3)
где ![]() ,
, ![]() , и
, и ![]() -
активные проводимости ветвей;
-
активные проводимости ветвей; ![]() ,
, ![]() и
и ![]() -
реактивные проводимости ветвей;
-
реактивные проводимости ветвей; ![]() - комплексная
проводимость контура;
- комплексная
проводимость контура; ![]() ,
, ![]() - активные составляющие токов ветвей
(рис. 4.1, б);
- активные составляющие токов ветвей
(рис. 4.1, б); ![]() ,
, ![]() - реактивные составляющие токов
ветвей.
- реактивные составляющие токов
ветвей.
С учетом ![]() и
и
![]() определим проводимости ветвей
определим проводимости ветвей
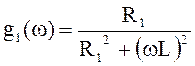 ,
,
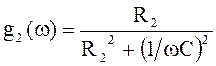 ,
, ![]() ; (4.4)
; (4.4)
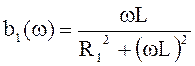 ,
,
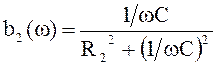 ,
, ![]() . (4.5)
. (4.5)
Токи ![]() и
и ![]() в параллельных ветвях контура могут
во много раз превышать входной ток, поэтому резонанс в параллельном контуре
называют резонансом токов. Отношение токов (коэффициент передачи по току)
является одной из важных частотных характеристик контура (например, между током
через ёмкость и входным током)
в параллельных ветвях контура могут
во много раз превышать входной ток, поэтому резонанс в параллельном контуре
называют резонансом токов. Отношение токов (коэффициент передачи по току)
является одной из важных частотных характеристик контура (например, между током
через ёмкость и входным током)
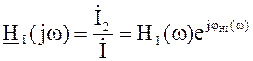 . (4.6)
. (4.6)
Входное комплексное сопротивление контура
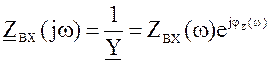 . (4.7)
. (4.7)
Комплекс действующего значения входного тока
![]() . (4.8)
. (4.8)
Комплексная АФЧХ для схемы рис 4.1,а
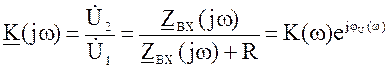 . (4.9)
. (4.9)
С учётом (4.4) и (4.5) можно определить частотные характеристики для параллельного контура
![]() ,
,
![]() ; (4.10)
; (4.10)
![]() ,
,
![]() ; (4.11)
; (4.11)
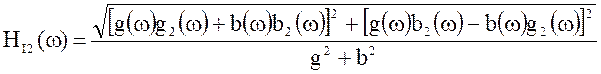 ;
;
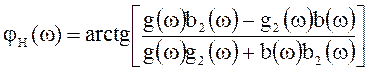 ; (4.12)
; (4.12)
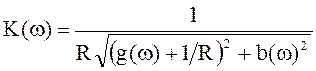 ;
;
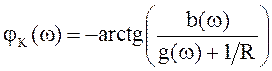 . (4.13)
. (4.13)
В резонансном режиме должно выполняться условие
![]() т.
е.
т.
е. ![]() и
и ![]() . (4.14)
. (4.14)
Из условия (4.14) с учетом ![]() и
и ![]() можно определить резонансную частоту для параллельного контура
можно определить резонансную частоту для параллельного контура
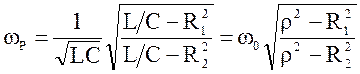 , (4.15)
, (4.15)
где ![]() и
и ![]() -
резонансная частота и характеристическое сопротивление последовательного
контура.
-
резонансная частота и характеристическое сопротивление последовательного
контура.
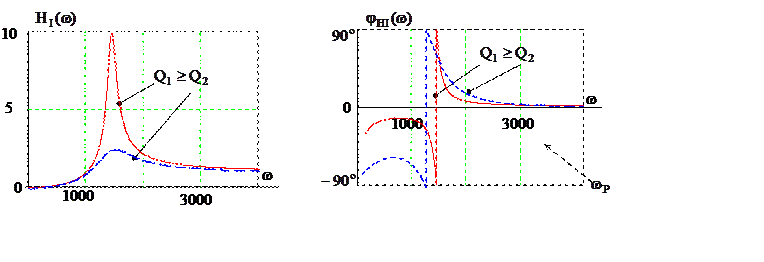 |
Рис. 4.2
Как видно из (4.15), резонансная частота ![]() , в отличие от частоты
, в отличие от частоты ![]() , зависит от активных потерь в
катушке индуктивности и ёмкости. Если потери в активных сопротивлениях контура
малы, то такой контур считается идеальным, а резонансные частоты
последовательного и параллельного контура совпадают
, зависит от активных потерь в
катушке индуктивности и ёмкости. Если потери в активных сопротивлениях контура
малы, то такой контур считается идеальным, а резонансные частоты
последовательного и параллельного контура совпадают ![]() . Анализ выражения (4.15) показывает,
что при значениях
. Анализ выражения (4.15) показывает,
что при значениях ![]() или
или ![]() резонанса в контуре не происходит.
резонанса в контуре не происходит.
На резонансной частоте реактивные проводимости ветвей
равны между собой ![]() и называются характеристической проводимостью параллельного
колебательного контура.
и называются характеристической проводимостью параллельного
колебательного контура.
Отношение действующего значения тока реактивного элемента к входному току параллельного колебательного контура на резонансной частоте называется добротностью параллельного колебательного контура
![]() . (4.16)
. (4.16)
На рис. 4.2 показаны передаточные частотные
характеристики по току (4.10) ![]() и
и ![]() параллельного контура. В резонансном
режиме характеристика
параллельного контура. В резонансном
режиме характеристика ![]() достигает
максимального значения, этот максимум определяет добротность контура и
показывает во сколько раз ток в реактивном элементе контура (например, в
ёмкости) больше входного тока. Фазочастотная характеристика
достигает
максимального значения, этот максимум определяет добротность контура и
показывает во сколько раз ток в реактивном элементе контура (например, в
ёмкости) больше входного тока. Фазочастотная характеристика ![]() в режиме, близком к резонансу, имеет
разрыв, т. е. значение разности фаз при переходе частоты
в режиме, близком к резонансу, имеет
разрыв, т. е. значение разности фаз при переходе частоты ![]() изменяется на
изменяется на ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.