Резонансные явления в параллельном колебательном контуре (Лабораторная работа № 4), страница 2

 

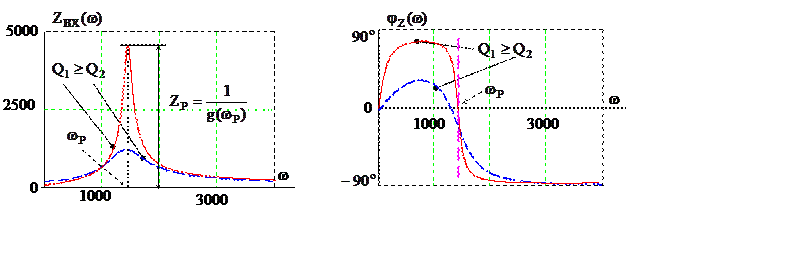
Рис. 4.3

 

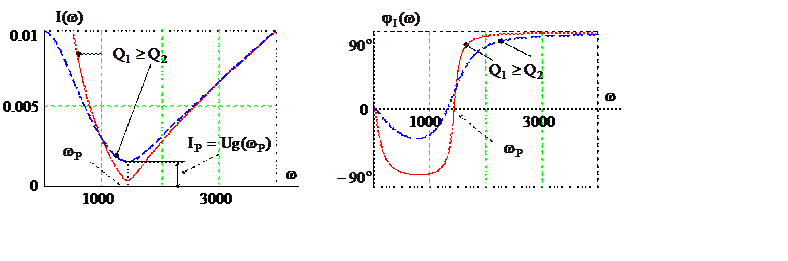Рис. 4.4

На рис. 4.3 показаны частотные характеристики входного сопротивления (10)  и  параллельного контура. В резонансном режиме модуль входного сопротивления достигает максимального значения , а у идеального контура его значение равно бесконечности. ФЧХ показывает, что при изменении частоты   входное сопротивление носит индуктивный характер, а в диапазоне  - ёмкостной.

На рис. 4.4 показаны частотные характеристики входного тока (4.11)  и  параллельного контура. Минимального значения ток достигает при резонансе, а его численное значение определяется величиной активной проводимости контура: .

На рис. 4.5 показаны характеристики ЛАЧХ -  и ФЧХ -  передаточной функции по напряжению, рассчитанные по формулам (4.13) для параллельного контура, включенного последовательно с резистором R (рис. 4.1,а). По этим характеристикам может быть определена полоса пропускания (П) .

 

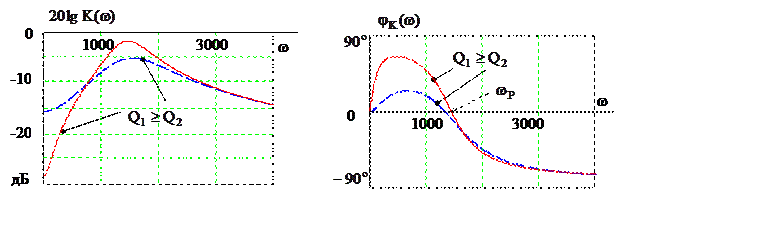Рис. 4.5

Для контуров, имеющих высокое значение добротности   ( >>  и  >> ), добротность - Q, резонансные частоты последовательного -  и параллельного колебательного контуров совпадают с , а значение характеристического сопротивления .

Для увеличения добротности параллельного резонансного контура сопротивление в ветви с конденсатором полагают равным нулю , а в ветви с катушкой индуктивности оставляют только активное сопротивление провода обмотки.

Для расчета частотных характеристик (4.10) ¸ (4.13) контуров с высокой добротностью  и  в режиме, близком к резонансу, можно пользоваться приближенными формулами:

входное сопротивление 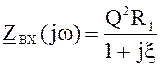                       ;                                                                      (4.17)

коэффициент передачи по току 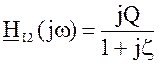          ,                                                                       (4.18)

где  - добротность контура, - обобщенная расстройка;  - резонансная частота. Добротность контура определяет полосу пропускания .

Для увеличения добротности контура вместо катушек индуктивности используют электронное устройство (гиратор - инвертор сопротивления), выполненное с применением операционных усилителей. Такого рода устройства называются активными фильтрами. Индуктивность гиратора может достигать тысяч Генри при меньших габаритах, по сравнению с обыкновенными катушками индуктивности.

4.2.  Программа подготовки к работе

При подготовке к лабораторной работе каждый студент должен изучить разделы курса ОТЭЦ [1], § 5.1¸5.6, ответить на вопросы одного из вариантов и результаты занести в соответствующие графы табл. 2 и 3 Исходные данные к расчетам и опытам приведены в табл. 4.1.

Для всех расчетов                                                                                                    Таблица 4.1

Номер стенда		R	Для всех вариантов. Индуктивность и активное сопротивление катушки:  = 15 мГн  = 12 Ом
	мкФ	Ом
1	0.033	900
2	0.01	1000
3	0.022	1500
4	0.01	600
5	0.022	1200
6	0.033	1400
7	0.022	700
8	0.033	1300
9	0.01	800
10	0.022	1100

     Вариант 1

    Для схемы рис. 4.6 определить резонансную частоту  и , а также для частоты  и переменное сопротивление R = 0 определить комплексы действующих значений токов , , , входное сопротивление  и значение комплексной передаточной функции по току - . Определить значения добротности контура - Q и характеристической проводимости - s.

    Задать величину сопротивления R из табл. 4.1 и рассчитать комплекс действующего значения выходного напряжения , передаточную функцию по напряжению - , значения характеристик ЛАЧХ - и ФЧХ - .

    Результаты расчета внести в табл. 4.2 и 4.3.

2

    Для рассчитанного режима построить векторные диаграммы токов и напряжений.