Диффузия в темаллах и сплавах, страница 7

                                                                    (7.35)

где  С – концентрация газа в объеме; С₀ – концентрация газа у поверхности.

Различают два периода дегазации.

Первый, когда зарождаются пузырьки газа. На этой стадии контролирующим является перенос газа из объема жидкого ме6талла к пузырькам. Это чаще всего процесс молекулярной диффузии, скорость которого определяется коэффициентом диффузии газа, числом пузырьков и характеристиками расплава.

На втором этапе дегазации число мест, где зарождаются пузырьки, сокращается. Пузырьки всплывают на поверхность, при этом важную роль играет перемешивание.

Рассмотрим вначале абсорбцию газа А в ламинарно стекающую пленку жидкости В. Вещество А  слабо растворимо в В, так как вязкость жидкости заметно не изменяется.

Будем считать, что диффузия в жидкой пленке носит медленный характер, поэтому расстояние, на которое проникают атомы А в пленку мало по сравнению с ее толщиной (δ). Профиль скоростей пленки υ_х(х) изображен на рис. 7.7 и аппроксимируется выражением

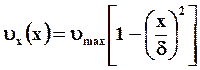                                                                        (7.36)

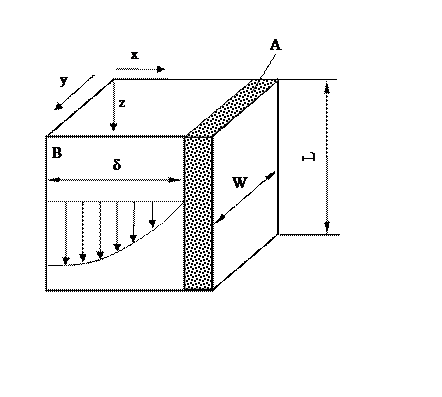
Рис.7.7.  Профиль скоростей в жидкой пленке

Из условия баланса вещества имеем

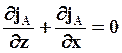                                                                                      (7.37)

где j_A – поток вещества А в пленку жидкости В.

Поток вещества А в направлении оси z определяется в основном движением пленки, поэтому

                                                                            (7.38)

Поток вещества А в направлении оси х переносится в основном вследствие диффузии, так как из-за малой растворимости А  и  В конвективный перенос практически отсутствует. Следовательно

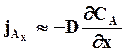                                                                                            (7.39)

Подставляя уравнение (7.37) и (7.38) в (7.39) получим дифференциальное уравнение

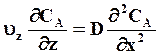                                                                                        (7.40)

Комбинируя уравнения (7.36) и (7.40), получим

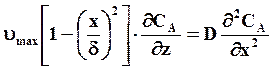                                                                   (7.41)

Рассмотрим вариант решения уравнения (7.41) для следующих граничных условий

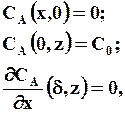
которое означает, что пленка жидкости в плоскости z = 0, когда она впервые соприкасается с веществом А, состоит из чистого вещества В, а концентрация А на поверхности раздела фаз в жидкости равна растворимости А и В (С₀).

Для случая малых времен контакта () стекающую пленку можно рассматривать как «бесконечно толстую» и движущуюся со скоростью υ_max, поскольку за малое время контакта вещество А «не заметит» разницы в скорости. Тогда уравнения (7.41) можно рассматривать в виде

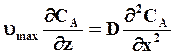                                                                             (7.42)

при этом третье граничное условие принимает выражение .

Решение уравнения (7.42) имеет вид

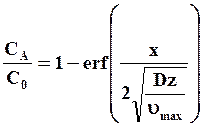                                                                          (7.43)

Поток вещества на поверхности ч = 0 в точке z равен

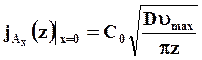                                                                           (7.44)

Интегрируя это выражение по площади контакта жидкой пленки, найдем общее количество вещества А, переходящего в единицу времени из газа в жидкую пленку

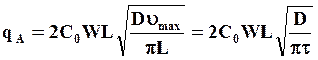                                                (7.45)

Из (7.45) следует, что скорость массообмена пропорциональна корню квадратному из коэффициента диффузии и обратно пропорциональна корню квадратному из времени контакта.

Используя уравнение (7.45) средняя скорость абсорбции газа на единицу поверхности контакта равна

                                                                        (7.46)

Для случая абсорбции газа жидкостью из всплывающих пузырьков можно заменить время контакта

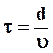
где d – диаметр пузырька; υ – скорость всплывания пузырька.

Тогда

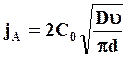                                                                                             (7.47)