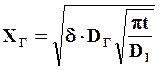Диффузия в темаллах и сплавах, страница 4

                                                                            (7.11)

где δ – ширина границы; D_Г  - коэффициент диффузии вдоль границы зерна; D_l – коэффициент объемной диффузии.

7.5.  Экспериментальное определение коэффициента диффузии

Экспериментальное определение коэффициента диффузии основано на анализе кривых распределения концентрации диффузанта вдоль ширины диффузионной зоны. Кривые распределения записывают с помощью микроанализаторов на специальных образцах с покрытием, подвергнутых отжигу при фиксированных температурах. На рис. 7.2 представлены типовые кривые распределения диффундирующих элементов по ширине диффузионной зоны.

По ширине диффузионной зоны можно рассчитать коэффициент диффузии для заданной температуры по формуле

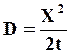                                                                                              (7.12)

где Х – ширина диффузионной зоны; t – длительность нагрева.

В результате измерений получают совокупность значений коэффициентов диффузии для различных температур и времени отжита.

Коэффициент диффузии описывается уравнением (7.9), которая после логарифмирования принимает вид

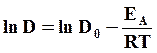                                                                            (7.13)

В координатах «lnD – 1/(RT)  выражение (7.13) носит линейный вид, который можно рассчитать по экспериментальным результатам (рис.7.3).

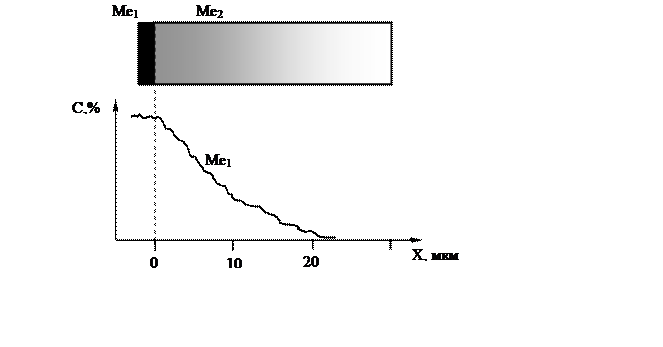
Рис. 7.2. Кривые распределения концентрации диффундирующих элементов по ширине диффузионной зоны

Рис. 7.3. К определению параметров уравнения коэффициента диффузии

Отрезок ординаты, отсекаемый прямой Аррениуса при  1/(RT) = 0, дает значение D₀ (точнее lnD₀), а тангенс угла наклона определяет энергию активации.

7.6.  Методы решения дифференциального уравнения диффузии.  

Методика построения диффузионных диаграмм

Теоретический анализ диффузионных процессов базируется на решении дифференциального уравнения (7.6), который с учетом условия (7.8) сводится к одномерной задаче. Поверхность, через которую осуществляется диффузионный массоперенос, представляют в виде прямой плоскости, при этом массовый поток направляется в глубь полубесконечного тела (рис.7.4). Температура процесса и коэффициент диффузии постоянны во времени. Решение дифференциального уравнения сводится к нахождению закона изменения концентрации диффундирующего элемента по глубине полубесконечного тела в зависимости от времени процесса С(Х, t)/

Итак, в одномерном варианте уравнение Фика второго рода представляется в виде

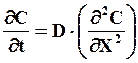                                                               (7.14)

Рассмотрим основные варианты решения диффузионных задач.

1. Диффузия в полубесконечный образец с нулевой начальной концентрацией диффузанта С(Х, 0) = 0 из другого полу ограниченного образца с начальной концентрацией С₀. Решение принимает следующий вид

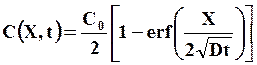                                             (7.15)

Концентрационные кривые представлены на рис. 7.5.

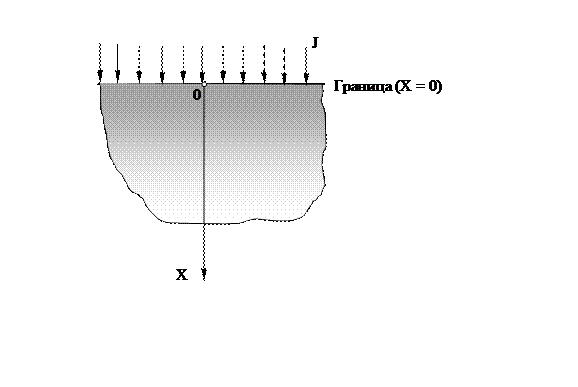
Рис. 7.4. Одномерная диффузионная модель

2. Диффузия в образец с нулевой начальной концентрацией через поверхность (Х = 0), на которой поддерживается постоянная концентрация С₀, не зависящая от времени, т.е. С(0,t) = C₀. закон распределения концентрации диффундирующего элемента описывается выражением

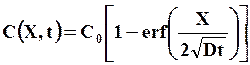
                                            (7.16)

Обратной этой задаче является вариант диффузии из полуограниченного образца с начальной концентрацией С₀ через поверхность (Х = 0) в среду, не содержащего диффундирующего вещества, т.е. на поверхности всегда поддерживается нулевая концентрация С(0,t) = 0. Решение принимает следующий вид

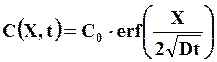                                                       (7.17)

3. Диффузия из образца с заданной начальной концентрацией С₀ через поверхность (Х =0), на которой массообмен происходит по закону

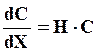                                                                               (7.18)

где Н – const.

Решение принимает вид

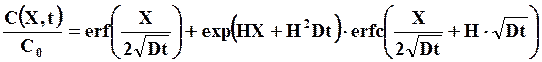                   (7.19)

На самой поверхности (Х = 0)концентрация меняется по закону