Остаточный член ряда Фурье. Погрешности приближения функций. Численное дифференцирование

12.Остаточный член ряда Фурье.

Для функции  f(x) Î L₂[a,b] обобщенный ряд Фурье сходится к ней в среднеквадратичном смысле и методическая погрешность аппроксимации может быть определена выражением  (1.48)

Представим

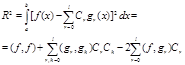Имея ввиду, что функции g_r(x), rÎ[0,l] ортогональны, а коэфиценты Фурье вычисляются по соотношению (1.51) получим 

oткуда

(1.54)

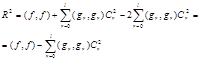а если g_r(x), rÎ[0,l] ортонормированные, то

(1.55)

Если на приближаемую функцию наложить дополнительные ограничения, то обобщенный ряд Фурье может сходиться к ней и в равномерном смысле. Например, необходимым и достаточным условием равномерной сходимости обобщенного ряда Фурье по полиномам Лежандра или Чебышева к f(x) на [a,b]. Независимо от типа сходимости, иногда оказывается необходимо оценить погрешность аппроксимации на [a,b] в виде максимального отклонения ряда Фурье от приближаемой f(x), что можно осущесвить дав оценку остаточного члена ряда Фурье

(1.56)

Однако в общнм случае аппроксимации таких оценок не существует. В частности, же, например, для (l+1) раз дифферинцируемых функций f(x), xÎ[a,b]

(1.57)

где a(x) – значение частичной суммы ряда Фурье на [a,b].Если более конкретизировать

задачу аппроксимации, положив в качестве базисных функций ряда Фурье полиномы Чебышева, то

(1.58)

Оценка остаточного члена ряда Фурье для непрерывной, преиодической, периода 2p функции f(x)

(1.59)

где K – некоторая константа, определение которой, вообще говоря, проблематично, l - максимальное значение скорости изменения f(x) на интервале аппроксимации. Оценки   (1.57) ¸(1.59) являются неконструктивными, поскольку содержат в себе параметры, определение которых практически невозможны или вызывают существенные трудности. Представляется целесообразным в случае неоходимости оценку остаточного члена (1.56) давать по некоторой модели аппроксимируемой функции, которая принадлежит к тому же классу, что и f(x), но в то же время является наиболее неблагоприятной в отношении точности аппроксимации. Учитывая наиболее вероятную с практической точки зрения априорную информацию об аппроксимируемой функции, за такую модель может быть принята функция вида

(1.60)

где f_min  и f_max – минимальное и максимальное значение f(x) на [a,b], W_М – максимальное значение круговой частоты спектра аппроксимируемой функции, если таковая информация может быть получена, или              

W_М  = V_М / A_М

где V_М – максимальная скорость изменения f(x) на [a,b]. При аппроксимации модели (1.60) обобщенными рядами Фурье по полиномам Лежандра и Чебышева первого рода были получены экспериментальные номограммы

которые позволили дать оценки остаточных членов в следующем аналитическом виде

(1.61)

где K≈0,212(5,3125 + l) для полиномов Лежандра и K_l =4 для полиномов Чебышевва. Следует отметить, что модельная оценка (1.61) совпадает с оценкой (1.58), если модели положить  A_М = 1,

a

имея в виду, что

13.Погрншности приближения функций.

Результирующая погрешноси приближения функции f(x), xÎ[a,b] в виде некоторой F(x), xÎ[a,b]  вобщем случае складывается составляющих .

1. Методическая погрешность используемого способа приближения, возникающая из-за отбрасывания остаточного члена при опрнделении F(x). Данная погрешность уменьшается с увеличением числа слагаемых в F(x), и в ряде случаев её удаётся оценить.

2. Погрешность приближенных вычислений ЭВМ, которые, в свою очередь, можно подразделить на две группы:

  Методическая погрешность, возникающая в результате использования численных методовпри реализации алгоритмов вычислений требуемых параметров. Данная погрешность имеет место, например, при исппользовании квадратурных формул численного интегрирования для определения коэфициентов Фурье. Эта погрешность может быть уменьшена за счет использования более точного вычислительного алгоритма и оценена в виде методической погрешности данного алгоритма.

   Вычислительная погрешность, порождаемая конечностью разрядной сетки памяти ЭВМ и зависящая (при выбранном алгоритме) от возможностей используемой вычислительной техники.

3. Погрешность от неточного задания исходных данных, которая носит случайный характер и может быть оценена вероятностными характеристиками. На пример, при аппроксимации  некоторой функции  f_*(x)=f(x)+ sf(x), где sf(x) – погрешности, искажающие истинную  f(x) и характеризуемые математическим ожиданием М{sf(x)}=0  и дисперсией D{sf(x)}=s², увеличение числа учитываемых членов ряда Фурье приводит к тому, что математическое ожидание случайной погрешности определения коэффициентов Фурье остаётся нулевым, а вот дисперсия возрастает.

   Анализируя поведение приведённых погрешностей в зависимости от числа слагаемых в приближающей F(x), можно сделать вывод, что увеличение количества учитываемых членов в F(x) приводит к тому, чтометодическая погрешность приближения уменьшается, в то время как все остальные, связанные, как правило, свычислением коэфициентов приближающей функции, возрастает. Таким образом, существует некое оптимальное значение числа учитываемых членов функции F(x), превышение которого приведёт к увеличению результирующей погрешности, поскольку скорость нарастания вычислительной погрешности становится больше, чем скорость уменьшения методической.