НГТУ
по вычислительной математике
Выполнил: Преподаватель:
студент Чикильдин Г.П
группы АП019
Малыгин Иван
Вариант №9
Новосибирск, 2002 г.
I. Цель: Исследовать влияние числа учитываемых членов ряда Фурье на точность аппроксимации. Определить погрешность аппроксимации.
Постановка задачи: На интервале [a,b] произвести
аппроксимацию функций f(t), заданной шагом ![]() ,
обобщённым рядом Фурье по системе ортогональных (ортонормированных) на [a,b] c весом
,
обобщённым рядом Фурье по системе ортогональных (ортонормированных) на [a,b] c весом
![]() базисных функций
базисных функций ![]()
Данные:
Функция: ![]()
Интервал: ![]()
Шаг: 0,05
Система
линейно независимых функций ![]() называется
ортогональной на
называется
ортогональной на ![]() с весом
с весом ![]() ,
если
,
если 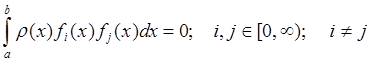 .
.
![]() - нормирующая функция. Она неотрицательна
на
- нормирующая функция. Она неотрицательна
на ![]() и интегрируема на
и интегрируема на ![]() с
положительным результатом.
с
положительным результатом.
Если для ортогональной системы выполняется условие
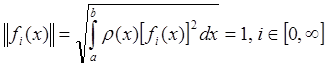 , то такая система функций называется
ортонормированной.
, то такая система функций называется
ортонормированной.
Пусть на ![]() задана система линейно независимых функций
задана система линейно независимых функций
![]() и некоторая последовательность констант
и некоторая последовательность констант ![]() Ряд вида
Ряд вида 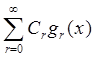 называется
функциональным рядом. Если этот ряд сходится, то его сумму обозначают как
называется
функциональным рядом. Если этот ряд сходится, то его сумму обозначают как ![]() .
.
Если
система функций ![]() будет ортогональна или
ортонормированна, то получаемый функциональный ряд будет называться рядом
Фурье.
будет ортогональна или
ортонормированна, то получаемый функциональный ряд будет называться рядом
Фурье.
Коэффициенты
![]() , коэффициенты Фурье, в таком случает будут
определяться так:
, коэффициенты Фурье, в таком случает будут
определяться так:
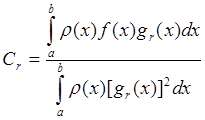 в случае ортогональной системы функций,
в случае ортогональной системы функций,
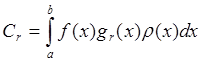 в случает ортонормированной системы.
в случает ортонормированной системы.
Произвольную
кусочно-непрерывную функцию ![]() на [a;b]
приближённо можно представить в виде обобщённого ряда Фурье с конечным числом
членов
на [a;b]
приближённо можно представить в виде обобщённого ряда Фурье с конечным числом
членов
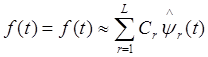 , (**)
, (**)
где ![]() ,
, ![]() – система
ортогональных на [a;b] базисных функций, а
– система
ортогональных на [a;b] базисных функций, а
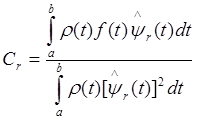 – коэффициенты Фурье . (*)
– коэффициенты Фурье . (*)
Таким
образом, чтобы решить задачу аппроксимации функции f(t) на
[a;b], необходимо при заданном базисе ![]() ,
, ![]() ,
, ![]() , вычислить коэффициенты Фурье
, вычислить коэффициенты Фурье ![]() согласно (*) и восстановить оценку
согласно (*) и восстановить оценку ![]() , аппроксимируемой функции f(t) по
(**).
, аппроксимируемой функции f(t) по
(**).
Полиномы
Лежандра, ортогональные на ![]() с весом
с весом ![]()
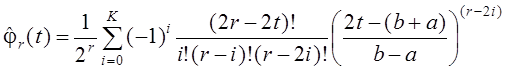 ,
, ![]()
К – целая часть
![]()
Нормирующий множитель полиномов Лежандра
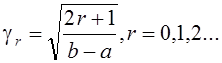 и ортонормированные полиномы -
и ортонормированные полиномы - ![]()
III. Листинг
program main
real f(113),t(113),ro(113),fi(7,113),f1(113),c(7),ff(113)
real a,b,dt,e(113),em,es,ep,emo,eso,epo,ff1(113)
real ff3(113),ff5(113),e1(113),e3(113),e5(113)
integer i,kon,l
open (1,file='data')
write (1,*)'Студент:Малыгин Иван'
write (1,*)'Группа: АП-019'
write (1,*)'Вариант №9'
write (1,*)'Исходные данные:a=0,6;b=2,05;dt=0,025;'
write (1,*)'аппророксимируемая функция:5+2,5*SIN(0,5*t);'
write (1,*)'базисные функции Лежандра.'
a=0.8
b=6.4
dt=0.05
kon=(b-a)/dt+1
do 1 i=1,kon
c Вычисление реализации аппроксимируемой
c функции f(t) на заданном [a,b] при фиксированном dt
t(i)=0.8+0.05*(i-1)
f(i)=5+2.5*sin(0.5*t(i))
1 continue
open (4,FILE='graph3')
do 2 l=1,7
c Вычисление базисных функций полинома Лежанжра
call n1yplg(a,b,kon,dt,l,ro,fi)
c Вычисление коэффициентов Фурье
call n1ykf(kon,dt,l,f,f1,fi,ro,c)
c Реализация оценки аппроксимируемой функции f~(t)
call n1ywst(kon,l,c,fi,ff)
c Вычисление погрешности аппроксимации
call n1yeee(f,ff,kon,e,em,es,ep,emo,eso,epo)
if(l.gt.2) write (4,*)l,emo,eso
write (1,10)l
write (1,11)
write (1,16)
write (1,12)
do 4 i=1,l
write (1,13)i,c(i)
4 continue
write (1,14) l-2,l
do 3 i=1,kon
if ((l.eq.4).or.(l.eq.6)) go to 7
if (l.eq.3) ff1(i)=ff(i)
if (l.eq.3) e1(i)=e(i)
if (l.eq.5) ff3(i)=ff(i)
if (l.eq.5) e3(i)=e(i)
if (l.eq.7) ff5(i)=ff(i)
if (l.eq.7) e5(i)=ff(i)
7 write (1,15) t(i),f(i),ff(i),e(i)
3 continue
2 continue
close(4)
write (1,11)
write (1,17)
write (1,19)
c Вывод в файл graph1 значений функции и аппроксимирующих
с полиномов
open(2,FILE='graph1')
do 8 i=1,kon
write (2,23)t(i),f(i),ff1(i),ff3(i),ff5(i)
8 continue
open(5,FILE='graph4')
c Вывод зависимости погрешности аппроксимирующих полиномов от
с аргумента
do 9 i=1,kon
write (5,*)t(i),e1(i),e3(i),e5(i)
9 continue
open (3,FILE='graph2')
c Вывод в файл graph2 реализации базисных фунций и весовой
c функции
do 5 i=1,kon
write (1,18)t(i),(fi(j,i),j=1,5)
write (3,23)t(i),(fi(j,i),j=1,5),ro(i)
5 continue
close (3)
write (1,11)
write (1,20)
write (1,21)
do 6 i=1,kon
write (1,22)t(i),ro(i)
6 continue
close (1)
close(2)
10 format ('Количество учитываемых членов ряда Фурье:',I1)
11 format (1x/'__________________________________________')
12 format ('Коэффициенты Фурье:')
13 format ('c(',I1,')=',f6.4)
14 format (1x/'Табл.',1x,I1/8x,'Результаты расчетов при l=',I1/3x, * 'T',9x,'F',10x,'~F',10x,'E')
15 format (F8.5,3x,F8.5,3x,F8.5,3x,F8.5,3x,F9.5)
16 format (1x)
17 format (1x/'Табл. 6'/11x,*'Реализации первых пяти базисных функций')
18 format (F6.4,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5)
19 format (3x,'T',6x,'^T1',6x,'^T2',6x,'^T3',6x,'^Т4',6x,'^T5')
20 format (1x/'Табл. 7'/'Реализация весовой функции')
21 format (6x,'T',8x,'Po')
22 format (1x,F8.5,1x,F8.5)
23 format (F6.2,1x,6(F11.8,1x))
end
IV. Результаты.
Приведены
графики функций ![]() ,
, ![]() ,
, ![]() ,
, ![]() , а
также графики базисных функций
, а
также графики базисных функций ![]() и графики
относительной и абсолютной погрешностей (EMO и ESO). Т.к.
весовая функция
и графики
относительной и абсолютной погрешностей (EMO и ESO). Т.к.
весовая функция ![]() , она на графики не выводится. Поскольку у полиномов
при l>3достаточно
высокая степень приближения, также приведены графики зависимости погрешности от
t.
, она на графики не выводится. Поскольку у полиномов
при l>3достаточно
высокая степень приближения, также приведены графики зависимости погрешности от
t.
V. Заключение
1. Погрешности аппроксимации падают с увеличением числа L учитываемых членов ряда Фурье, но если при малых L это падение очень заметно, то при увеличении L оно начинает уменьшаться, что связано с возрастанием числа вычислительных операций и, следственно, накоплением вычислительной погрешности.
2. Ряды Фурье приближают функцию лучше в среднеквадратическом смысле, а не в равномерном, что видно из последнего графика: есо на порядок меньше, чем емо.
VI. Список литературы
Цель. Постановка задачи. 2
Теоретическая часть 2-3
Листинг 3-5
Результаты. Графики. 5-7
Заключение. 8
Список литературы. 8
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.