Ортогональные и нормированные системы

10. Ортогональные и нормированные системы.

Система  линейно  независимых  функций      принадлежащих

L[a,b],называется   ортогональной с  весом  p(x),если

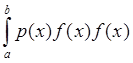=0,  i,j = 0,1,2,3,4….,,где  весовая  функция  p(x)  обладает  тем

свойством, что она  не  отрицательна  на  [a,b],интегрируема  на этом интервале и

ее  интеграл  положителен.

Если  выполняется  дополнительные условия, а  именно:

||f(x)||=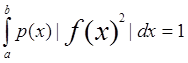,   i=0 , 1 , 2 , 3….,   то  система  функций ,  x[a,b],

i=0,1,2,3……, называется   ортонормированной  на [a,b] с весом  p(x).

В     матаматике  известен  целый  ряд  функций  так  называемых    классических

ортогональных  систем  функций, среди  которых  помимо полиномов Лежандра

 можно выделить  полиномы Чебышева первого рода, ортогональные и нормированные

на интервале [a,b]   с    весом :

             p(x)=1/,

функции  Лагерра, ортонормированные  на  [0,n] с весом   p(x)=1 ,   гармонические

 функции, ортонормированной  на [-п , п] с весом  p(x)=1.Однако  в практических

расчетах  используются  любые интервалы [a,b]  конечной  длины.

 1) Полиномы  Лежандра, ортогональные  на интервале [a,b]   с    весом  p(x)=1

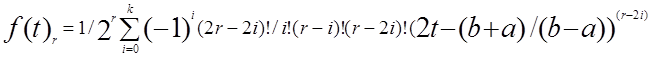
к=1,2,3,4….,  К - целая  часть  [r/2], 

 2)Полиномы Чебышева первого рода, ортогональные  на интервале [a,b]   с  весом   

p(x)=1/,

Определяются   согласно  выражению:

,

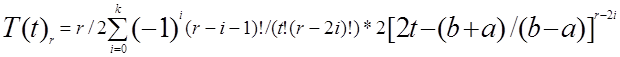 к=1,2,3,4….,  К - целая  часть  [r/2], 

 3)Функции  Лагерра, ортонормированные  на  [0,n] с весом   p(x)=1 ,

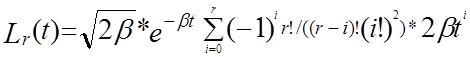
к=0,1,2,3….,

Параметр  ,необходимо выбрать из условия  сохранения свойств

функции  Лагерра  при  их   рассмотрении не на бесконечном интервале,

а на конечном  интервале  изменения аргумента t.

Экспериментально , было установлено, что  параметр   следует

выбирать  в  виде:

          ,

L -номер  последней  учитываемой  в  совокупности  функций Лагерра.