Умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах

Исходные данные:

Множитель=74,15

Множимое=65,97

Заданная кодировка множимого:"0" - 01;"1" – 00;"2" – 11;"3" – 10.

Кодировка множителя :традиционная(обычным весомозначным кодом):"0" – 00;"1" – 01;

"2" – 10;"3" – 11.

Алгоритм умножения: А.

Метод умножения: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах.

Тип структурной схемы:2.

Базис для реализации ОЧС: .

Базис для реализации ОЧУС:,.

Разработка алгоритма умножения:

1.Перевод чисел в четверичную систему исчисления:

 Мн10=74,1510       

 74| 4                                              0,15

 34|18| 4                                             4

    2|16|4| 4                                     0,60

         2|4|1                                            4

0  2,40         

                                                    4

                                               1,60

                                                   4  

                                              2,40

Мн4=1022,024  

Мн2/4=00 01 11 11,01 11 (кодируем используя заданную кодировку)

 Мт10=65,9710

 65| 4                                           0,97

 25|16| 4                                         4

   1|16|4| 4                                   3,88

        0|4|1                                          4

0  3,52

                                               4 

                                         2,08

 Мт4=1001,334

 Мт2/4=01 00 00 01,11 11 (закодировано традиционно)

2.Представление чисел в форме с плавающей запятой:

 Мн4=0,1022024         Рмн=410=104            

 Мн2/4=01,00 01 11 11 01 11    Рмн=0,00 01 (закодировано по заданию)

 Мт4=0,1001334                 Рмт=410=104

 Мт2/4=00,01 00 00 01 11 11     Рмт=0,01 00 (закодировано традиционно)

3.Производим умножение чисел:

   1)Найдём порядок произведения,для чего сложим мантиссы:

     Рмн =     104   0,00 012/4

     Рмт =     104   0,01 002/4

     Рмн*Мт  = 204   0,11 002/4

   2) Преобразуем множитель для умножения в прямых кодах:

      Мтпр.4=0,10020

      Мт_пр2/41=0,01 00 00 10 00

    3)Найдём знак произведения:

      зн Пр =зн Мнзн Мт=0  0 =0

 4)Умножим числа по алгоритму А:

      Мн=0,102202               

      2Мн=0,211010

      [-Мн]=3,231131

0,000000 3,231131		00,00 00 00 00 00 00 10,11 10 00 00 10 00		Σ0 П1=-Мн
3,231131 3,323113	1	10,11 10 00 00 10 00 10,10 11 10 00 00 10	00	Σ1 Σ1*4-1
3,332311	31	10,10 10 11 10 00 00	10 00	Σ2*4-1
0,211010 0,203321 0,020332 0,020332 0,002033 0,002033 0,000203	31 131 131 2131 2131 32131	01,11 00 00 01 00 01 01,11 01 10 10 11 00 01,01 11 01 10 10 11 01,01 11 01 10 10 11 01,01 01 11 01 11 11 01,01 01 11 01 11 11 01,01 01 01 11 01 11	10 00 00 10 00 00 10 00 11 00 10 00 11 00 10 00 11 11 00 10 00	П2=2*Мн Σ3 Σ3*4-1 Σ4= Σ3*4-1 Σ4*4-1 Σ5 Σ5*4-1
0,102202 0,103011 0,010301	32131 132131	01,00 01 11 11 01 11 01,00 01 10 01 00 00 01,01 00 01 10 01 00	10 11 00 10 11 00 10 11 00 10 11	П6 Σ6 Σ6*4-1

  5)Найдём погрешность операции:

    Мн₁₀*Мт₁₀=4891,6755₁₀

    Мн₄*Мт₄=1030113,2132₄=4887,566₁₀   

    = = 4,109092 –абсолютная погрешность

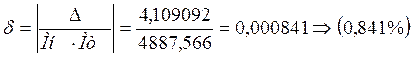     -относительная погрешность

Синтез  ОЧС:

1)Функция S₁ (старший разряд диады суммы ) после минимизации имеет вид:

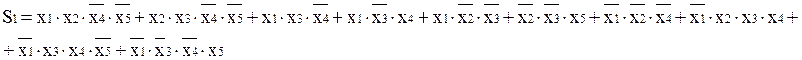
После приведения к необходимому базису имеем:

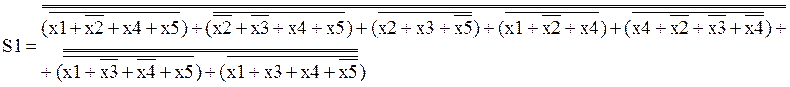
Эффективность минимизации:

2) Функция S₂ (младший разряд диады суммы) после минимизации имеет вид:

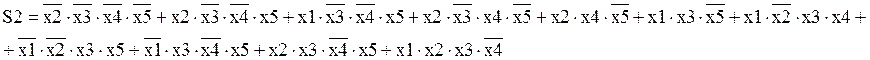
После приведения к соответсвующему базису:

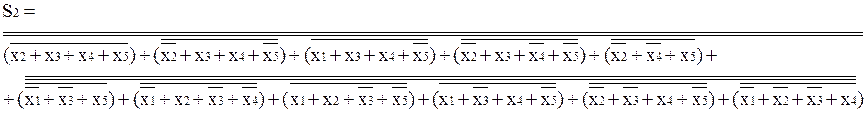
Эффективность минимизации:

3)Функция Р (перенос) после минимизации имеет вид:
 

После приведения к соответствующему базису функция имеет вид:

 

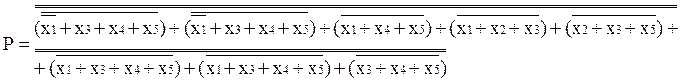
Эффективность минимизации:

Синтез ОЧУС:

1)Минимизация функции переноса:

L=101000 ;111000 ;101010 ;111010 .

N=xxx011 ;xx0x1x ; xx11xx. (Предварительно склеенные безразличные наборы.)

Выполняем операцию "*":

Перемножаем множество C₀*C₀(таблица 1.1)С₀=L∩N:

Z₀=ø

A₁=1x1000;101x00;111x00;1110x0;10101x;10x010;101x10;1x1010;11101x;111x10

Перемножаем множество С₁*С₁ (табл. 1.2).С₁=А₁:

Z₁=10101x

A₂=10xx10;1x1x00;101xx0;111xx0;1x101x;101x1x;10xx10;1x1x10;111x1x

Перемножаем множество С₂*С₂ (табл. 1.3) .С₂=А₂:

Z₃=1x10x0;1x101x;101x1x

A₃=1x1xx0;1x1x1x

Перемножаем С3*С3 (табл. 1.4).С₃=А₃:

Z₄=1x1xx0;1x1x1x

Таким образом:

Z=10101x;1x10x0;1x101x;101x1x;1x1xx0;1x1x1x – множество простых импликант

После выполнения операции "#"(табл. 1.5) находим L-экстремали : E=1x1xx0;1x1x1x.

После выполнения операции L ∩ E (табл. 1.6)находим ,что обязательных L-экстремалей нет.

После операции L ∩ Z (табл. 1.7) находим наилучшую минимальную форму:

1х1хх0

Эффективность минимизации:

2)Минимизация Q1(старшего разряда диады результата):

L=000101;100001;100100;100101;101000;101001;110001;110100;110101;111001;

001010;101010

N=xxx011;xx0x1x;xx11xx (Предварительно склеенные безразличные наборы)

Выполняем операцию "*":

Перемножаем С₀*С₀ (табл. 2.1).С₀=L∩N:

Z₀= ø

A₁=x00101;0001x1;00x101;100x01;10x001;1x0001;1000x1;10010x;1x0100;1001x0;

10x100;1x0101;1001x1;10x101;10100x;1010x0;101x00;1x1001;1010x1;101x01;

110x01;11x001;1100x1;11010x;1101x0;11x100;1101x1;11x101;1110x1;111x01;

xx0011;x01010;00101x;00x010;001x10;10x010;101x10;xx1x11;xxx11x

Выполняем операцию С₁*С₁ (табл. 2.2).С₁=А₁:

Z₁= ø