Анализ и оптимизация систем на основе моделей массового обслуживания

станки В1 и В2, время обработки одной детали на которых распределено по экспоненциальному закону и составляет в среднем 12 минут. Накопитель перед станками В1 и В2 вмещает 5 деталей.

Время обработки деталей на станке С – 7 мин.

1. Характеристики работы станка А.

Интервалы времени между заявками распределяются по экспоненциальному закону (пуассоновский поток). Время обслуживания заявок распределяется по равномерному закону. Следовательно, СМО мы можем обозначить следующим образом – М/G/1, где 1 – количество каналов обслуживания.

Заготовки для выпуска деталей поступают на участок в среднем через каждые 6 мин. Следовательно, интенсивность распределения

 дет/мин

Т.к. распределение носит экспоненциальный характер, то коэффициент вариации интервалов времени между заявками

ν = 1

Т.к. время обслуживания заявок распределяется по равномерному закону, то коэффициент вариации времени обслуживания

ε = (5 – 2)/(5 – 2)*√3 = 3/12,12 = 0,25

Время обработки деталей на станке составляет от 2 до 5 мин. Следовательно, среднее время обслуживания детали на станке

мин

Тогда интенсивность обслуживания заявок (среднее количество заявок, которое может быть обслужено одним каналом СМО в единицу времени)

Найдем нагрузку на СМО (величина, представляющая собой отношение интенсивности потока заявок к интенсивности, с которой СМО может их обслуживать)

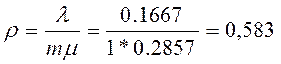
Т.к. ρ < 1, то наша СМО нормально работает.

Т.к. мы имеем дело с разомкнутой СМО без ограничений на очередь, то коэффициент загрузки U=, который показывает, какую часть от общего времени своей работы СМО выполняет обслуживание деталей.  U=0,583. Это означает, что СМО простаивает значительную часть времени, т.е. используется нерационально. (т.к. U < 0,75).

Найдем вероятность простоя СМО

Эта величина показывает, какую часть от общего времени работы СМО все ее каналы, т.е. станки, свободны, т.е. простаивают из-за отсутствия деталей.

Среднее число заявок в очереди (средняя длина очереди)

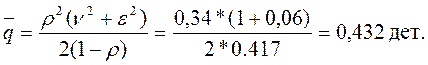
Среднее число заявок на обслуживании (т.е среднее число занятых станков)

Среднее число заявок в системе (т.е. в очереди и на обслуживании)

Среднее время ожидания в очереди (среднее время ожидания обслуживания)

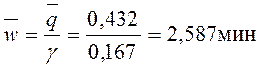
Среднее время пребывания в системе (т.е. в очереди и на обслуживании)

Пропускная способность системы (среднее число заявок, обслуживаемых в единицу времени)

,

т.к. система разомкнутая без ограничений на очередь.

2. Характеристики работы группы станков В1 – В2

Интервалы времени между заявками распределяются по экспоненциальному закону (пуассоновский поток). Время обслуживания заявок также распределяется по экспоненциальному закону и составляет в среднем 12 мин. Количество каналов обслуживания – 2 (два одинаковых станка). Перед станками стоит накопитель, вмещающий 5 деталей. Поэтому станки В1-В2 могут быть представлены как СМО типа М/М/2 с ограничением на длину очереди ().

Т.к. только 90% от деталей типа 1 поступают на обработку на станки В1-В2, то  интенсивность входного потока заявок  

Т.к. распределение носит экспоненциальный характер, то коэффициент вариации интервалов времени между заявками

ν = 1

Т.к. время обслуживания заявок распределяется по экспоненциальному закону, то коэффициент вариации времени обслуживания

Обработка одной детали занимает в среднем 12 мин, поэтому среднее время обработки детали мин, интенсивность обработки деталей на станках

Найдем нагрузку на СМО (величина, представляющая собой отношение интенсивности потока заявок к интенсивности, с которой СМО может их обслуживать)

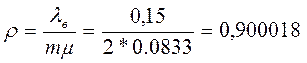
Вероятность простоя определяется по формуле:

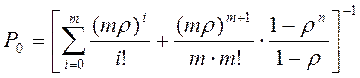
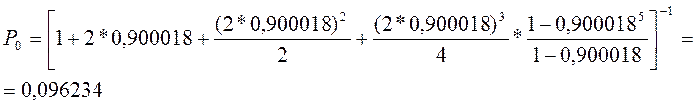
Т.о. всего 0,096234 от общего времени работы системы все ее каналы свободны, т.е. простаивают из-за отсутствия заявок.

Найдем вероятность отказа от выполнения заказа из-за занятости станков В1-В2 и наполнения накопителя:

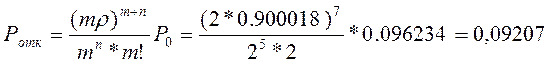
Т.о. 0,09207 всех поступающих заявок не обслуживается системой из-за занятости ее каналов или большого количества заявок в очереди.

Коэффициент загрузки системы

Т.о. 0,817154 от общего времени система выполняет  обслуживание заявок. Нормальный коэффициент загрузки – 0,75-0,85.  Это означает, что наша система используется рационально.

Среднее число заявок в очереди (средняя длина очереди)

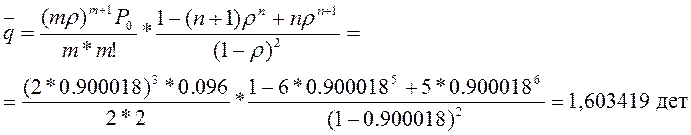
Среднее число заявок на обслуживании (т.е среднее число занятых станков)

Среднее число заявок в системе (т.е. в очереди и на обслуживании)

Среднее время ожидания в очереди (среднее время ожидания обслуживания)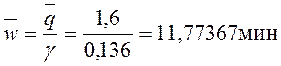                                           

Среднее время пребывания в системе (т.е. в очереди и на обслуживании)

Пропускная способность системы (среднее число заявок, обслуживаемых в единицу времени)

3. Проверка результатов на программе SMO.

Характеристики работы станка А

Итак, станок А 58,3% всего времени работы непосредственно обрабатывает