Моделирование условий выпуска деталей

Приведем условие задачи в виде схемы:

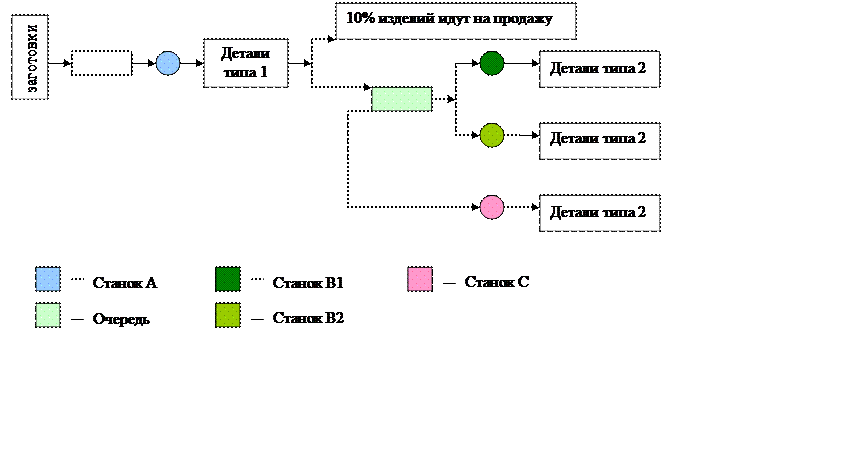
Заготовки поступают на станок А, в среднем, каждые 6 минут (пуассоновский поток) и время обработки детали составляет от 2 до 5 минут.

После обработки на станке А 10% деталей идет на продажу (как готовые детали типа 1), а остальные поступают на станки В1 и В2.

Время обработки детали на станках В1 и В2, в среднем, 12 минут (экспоненциальный закон). Общий накопитель для этих станков может вмещать до 5 деталей, а при его заполнении поступающие детали направляются на станок С.

Обработка детали на станке С занимает, приблизительно, 7 минут.

Таблица расходов в д.е.

	А	В	С
Работа	0,3	0,6	0,5
Простой	0,1	0,2	0,1

	Детали типа 1	Детали типа 2
Расходы, связанные с выпуском деталей (д.е.)	2	8
Рыночная цена деталей (д.е.)	5	22

1.  ХАРАКТЕРИСТИКИ РАБОТЫ СТАНКА А

Станок А можно рассматривать как СМО типа M/G/1 без ограничения на очередь: М означает, что временные интервалы между заявками (поступлением заготовок) распределены по экспоненциальному закону, G – время обслуживания распределено по равномерному закону, 1 – количество каналов (обслуживающих элементов) равно единице, т.е. заготовки обрабатывает один станок.

Заготовки поступают на обработку через каждые 6 минут. Значит, интенсивность потока заявок (среднее количество заявок в единицу времени):

 дет/мин.

Коэффициент вариации интервалов времени между поступлением заявок (величина, отражающая отклонение отдельных значений случайной величины от среднего значения : , где - стандартное отклонение случайной величины, а  - математическое ожидание средней случайной величины):

Т.к распределение носит экспоненциальный характер по условию.

Заготовки обрабатываются от 2 до 5 минут, значит, интенсивность обслуживания (количество деталей, обрабатываемое в единицу времени, при условии, что канал никогда не простаивает из-за отсутствия заявок):

А коэффициент вариации интервалов времени обработки заготовки:

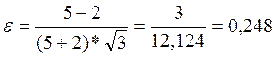
Т.к интервал времени обработки представляет собой случайную величину, распределенную по равномерному закону, в интервале [2;5].

Рассчитаем нагрузку на СМО:

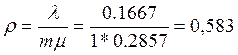
, т.е СМО справляется обслуживать заявки, и они не накапливаются.

Т.к наше СМО без ограничения на очередь, значит коэффициент загрузки U=, это означает, что 0,583 всего времени работы СМО выполняет обслуживание заявок, т.е. СМО простаивает значительную часть времени и используется нерационально.

Рассчитаем вероятность простоя:

Это означает, что 0,417 всего времени СМО простаивает из-за отсутствия заявок.

Рассчитаем среднее число заявок в очереди:

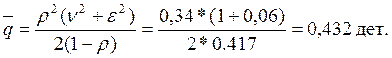
Рассчитаем среднее число заявок на обслуживание:

Среднее число заявок в системе:

Среднее время пребывания заявки в очереди:

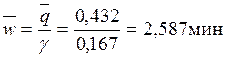
Среднее время пребывания в системе:

Пропускная способность (среднее число заявок, обслуживаемых в единицу времени) равна интенсивности потока заявок:

2   ХАРАКТЕРИСТИКИ РАБОТЫ СТАНКОВ В1 И В2.

Т.к. поток заявок пуассоновский по условию, время обработки детали на этих станках распределено по экспоненциальному закону и число обслуживающих элементов (станков) рано двум, то систему этих станков можно рассматривать как СМО типа М/М/2 с ограничением на очередь, т.к. накопитель вмещает только 5 заявок.

По условию задачи только 90% обработанных на станке А деталей подлежат дальнейшей обработке, т.е. интенсивность потока заявок на станки В1 и В2 составит 90% от интенсивности потока заготовок на станок А. ( Поток деталей пуассоновский по условию задачи):

Коэффициент вариации интервалов времени между поступлением заявок

Т.к распределение носит экспоненциальный характер.

Детали обрабатываются в среднем 12 минут, значит, интенсивность обслуживания:

А коэффициент вариации интервалов времени обработки детали:

Т.к распределение носит экспоненциальный характер.

Рассчитаем нагрузку на СМО:

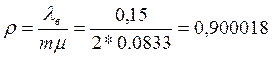
Рассчитаем вероятность простоя:

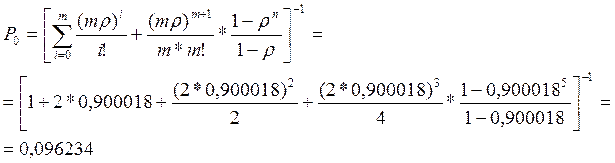
Где m-количество каналов, n– максимальное число элементов в очереди. Эта величина показывает, что только 10% от всего времени работы СМО простаивает, т.е. показатель достаточно неплохой.

Вероятность отказа:

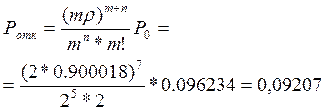
Это означает, что 0,092 всех поступающих деталей не обслуживается из-за занятости каналов.

Коэффициент загрузки:

Т.е. 82% от всего времени работы СМО обрабатывает детали.

Среднее число заявок в очереди:

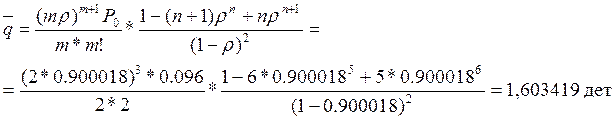
Рассчитаем среднее число заявок на обслуживание:

Среднее число заявок в системе:

Пропускная способность:

Среднее время пребывания заявки в очереди:

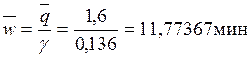
Среднее время пребывания в системе:

3  ПРОВЕРКА РЕЗУЛЬТАТОВ НА ПРОГРАММЕ СМО

Характеристики станка А:

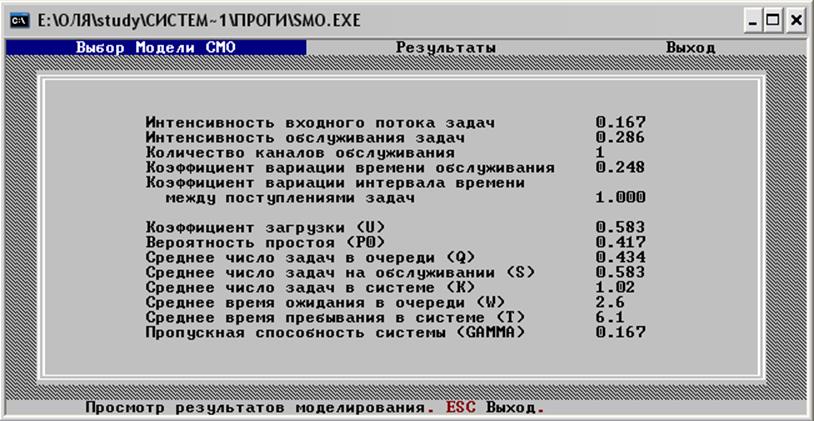
Таким образом, 58% всего рабочего времени станок А обрабатывает заготовки, 42% всего времени он простаивает из-за отсутствия заявок, что не очень хорошо. В среднем в очереди находится 0,43 заявки, а в очереди и на обслуживании 1,02 заявки. Станок обрабатывает в минуту в среднем 0,167 заготовок (все поступающие заявки). Время от поступления заявки до начала ее обработки составляет 2,6 минут, а время от поступления заявки до завершения ее обработки составляет 6,1 минут.

Характеристики станков В1 и В2

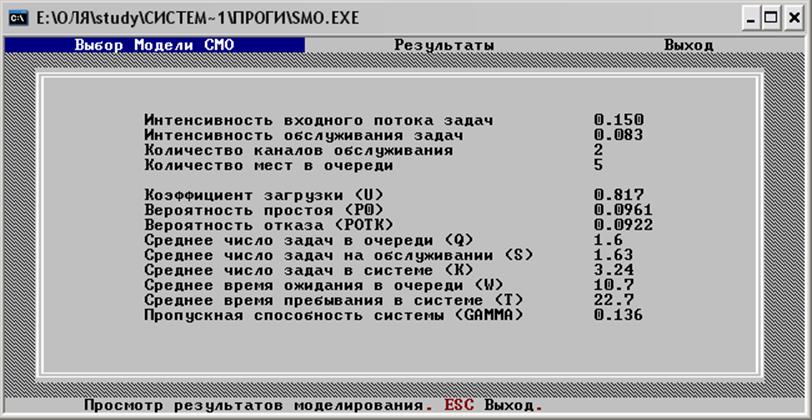
Таким образом, 81% всего рабочего времени станки В1 и В2 обрабатывают детали, 10% всего времени они простаивают из-за отсутствия заявок. В среднем в очереди находится 1,6 заявки, а в очереди и на обслуживание 3,24 заявки. Станки обрабатывают в минуту в среднем 0,136 детали, что объясняет появление очереди. Время от поступления детали до начала ее обработки составляет 10,7 минут, а время от поступления детали до завершения ее обработки составляет 22,7 минут.

4   ХАРАКТЕРИСТИКИ РАБОТЫ СТАНКА С