Математические модели в расчетах на ЭВМ
Практическое занятие № 2
тема: Решение ОДУ и краевых задач в MathCad
Выбрать пункт:
Примеры решения краевых задач
Индивидуальные задания
Контрольные вопросы
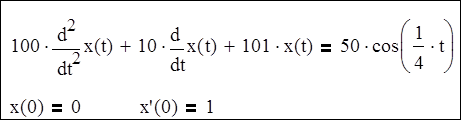
Порядок выполнения задания № 1 (Способ 1.)
![]() Набрать слово Given
Набрать слово Given
![]() Ниже введенного слова набрать левую часть уравнения
Ниже введенного слова набрать левую часть уравнения
![]() Выбрать логическое равно “=” из меню “Boolean” математической панели (либо Ctrl+=)
Выбрать логическое равно “=” из меню “Boolean” математической панели (либо Ctrl+=)
![]() Ввести правую часть уравнения
Ввести правую часть уравнения
![]() Аналогичным образом набрать граничные условия
Аналогичным образом набрать граничные условия
(для набора символа ‘ использовать комбинацию Сtrl+F7)
![]() Указать имя искомой функции и присвоить ему найденное решения,
возвращаемое функцией
Указать имя искомой функции и присвоить ему найденное решения,
возвращаемое функцией
Odesolve (x, b, [step]), где
x - имя переменной дифференцирования искомой функции (в данном случае t);
b – максимальное значение изменение переменной x (область поиска решения);
[step] – необязательный параметр, указывающий количество шагов внутри указанной
области.
Например: x :=Odesolve(t,150)
![]() Построить график полученного решения на интервале от 0 до 150;
Построить график полученного решения на интервале от 0 до 150;
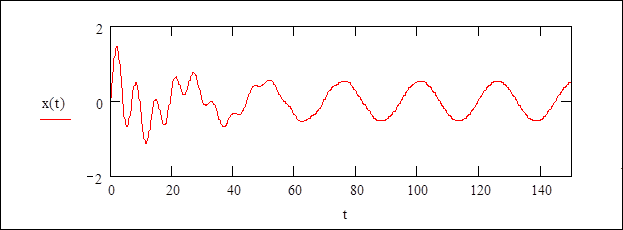
Порядок выполнения задания № 1 (Способ 2.)
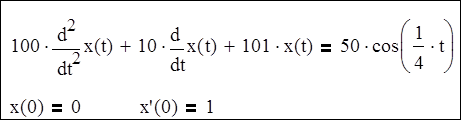
Приведем данную краевую задачу к виду:
Пусть x0(t)=x(t); x1(t)=x’(t)
Тогда можно записать:
x0’(t)=x1(t)
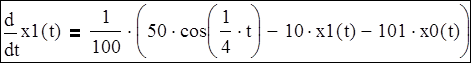
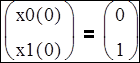
![]() Указать область поиска решения;
Указать область поиска решения;
Например: t0:=0 t1:=150
![]() Определить вектор начальных условий, в нашем случае их два, значит
вектор из двух значений
Определить вектор начальных условий, в нашем случае их два, значит
вектор из двух значений
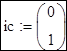
![]() Указать число шагов внутри указанной области (количество точек
расчета) N:=200;
Указать число шагов внутри указанной области (количество точек
расчета) N:=200;
![]() Задать вектор производных. Для данной задачи он имеет вид:
Задать вектор производных. Для данной задачи он имеет вид:
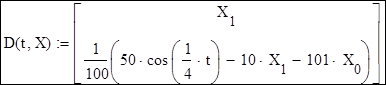
(набор индексов в переменной (X1) осуществлять как обращение к элементу (Xn) матрицы на панели Matrix)
![]() Найти решение краевой задачи с помощью функции Rkfixed(y, x1, x2, npoints, D), где
Найти решение краевой задачи с помощью функции Rkfixed(y, x1, x2, npoints, D), где
y - вектор начальных значений;
x1, x2 – начальная и конечные точки поиска решения;
npoints - количество точек расчета;
D - вектор производных задачи.
Например:
S:=rkfixed(ic,t0,t1,N,D)
S – возвращаемая матрица значений
![]() Переопределить матрицу найденных значений:
Переопределить матрицу найденных значений:
- Выделить вектор независимой переменной (t) T:=S<0>
- Выделить вектор значений искомой функции (x(t)) X:=S<1>
(S<0> означает обращение в первому (нулевому) столбцу возвращаемой матрицы значений, и
вводится данное обращение через панель Matrix и кнопку M<>)
![]() Построить график функции X(T)
Построить график функции X(T)
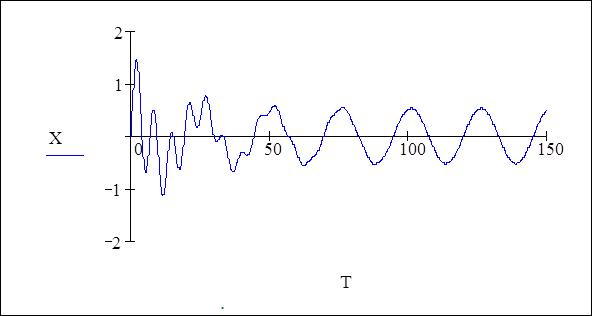
![]() Проверить найденное решение с решением, полученным в результате
первого способа решения.
Проверить найденное решение с решением, полученным в результате
первого способа решения.
Задание 1: Найти решение граничных задач двумя вышеописанными способами и сравнить найденное решение с точным решением.
u’’=2v
v’’=4v-2u
c начальными условиями u(0)=1.5, v(0)=1, u’(0)=1.5, v’(0)=1
Порядок выполнения задания 3
Приведем данную краевую задачу к виду:
Пусть y0(x)=u(x);
y1(x)=u’(x);
y2(x)=v(x);
y3(x)=v’(x);
тогда можно записатьy1’(x)=2y2(x), y3’(x)=4y2(x)-2y0(x) и соответственно граничные условия.
![]() Указать область поиска решения;
Указать область поиска решения;![]()
Например: x0:=0 x1:=1
![]() Определить вектор начальных условий, в нашем случае их два, значит
вектор из двух значений
Определить вектор начальных условий, в нашем случае их два, значит
вектор из двух значений
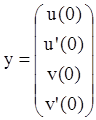 , т.е. указать
, т.е. указать 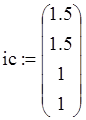
![]() Указать число шагов внутри указанной области (количество точек
расчета) N:=20;
Указать число шагов внутри указанной области (количество точек
расчета) N:=20;
![]() Задать вектор производных. Для данной задачи он имеет вид:
Задать вектор производных. Для данной задачи он имеет вид:
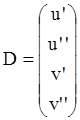 , т.е.
, т.е. 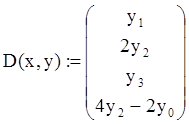
(набор индексов в переменной (X1) осуществлять как обращение к элементу (Xn) матрицы на панели Matrix)
![]() Найти решение краевой задачи с помощью функции Rkfixed(y, x1, x2, npoints, D), где
Найти решение краевой задачи с помощью функции Rkfixed(y, x1, x2, npoints, D), где
y - вектор начальных значений;
x1, x2 – начальная и конечные точки поиска решения;
npoints - количество точек расчета;
D - вектор производных задачи.
Например:
![]() ,
,
Z – возвращаемая матрица значений
![]() Переопределить матрицу найденных значений:
Переопределить матрицу найденных значений:
- Выделить вектор независимой переменной (x) X:=Z<0>
- Выделить вектор значений искомой функции (u(t)) U:=Z<1>
- Выделить вектор значений искомой функции (v(t)) V:=Z<3>
(Z<0> означает обращение в первому (нулевому) столбцу возвращаемой матрицы значений, и
вводится данное обращение через панель Matrix и кнопку M<>)
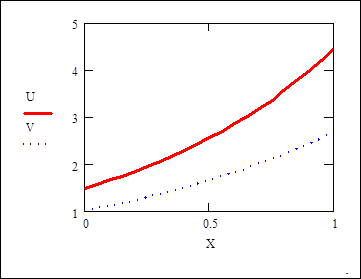
![]() Построить графики функции U(x) и V(x)
Построить графики функции U(x) и V(x)
(для построения на одной координатной оси двух графиков выделить имя первой функции и нажать ‘,’)
x’=-8x+8y
y’=30x+y-xz
z’=xy-2y
x(0)=-1
y(0)=0
z(0)=1
Порядок выполнения задания
(Способ 1) Применение функции Odesolve (x, b, [step]),
Пример:
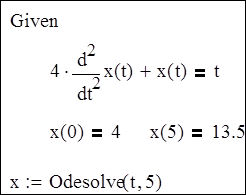
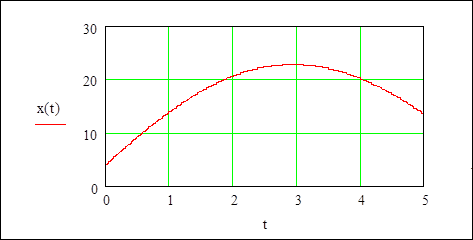
Построение графика функции x(t)
______________________________________________________________________________________
(Способ 2) Преобразование краевой задачи к задаче типа Коши (I этап) и ее решение с использованием функции rkfixed() (II этап)
I этап
Для приведения дифференциальной краевой задачи к виду Коши необходимо найти x’(0). Для этого зададим:
- стартовое значение поиска величины x’(0)
v0 := 4
- область поиска решения
t0:=0
t1:=5
- функцию производных
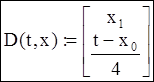
- неизвестные начальные условия, которые будут определены в дальнейшем с помощью sbval
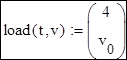
- разницу между вычисленными и заданными значениями x0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.