Решение ОДУ и краевых задач в MathCad (Практическое занятие № 2), страница 2

Определим недостающее значение x’(0), для этого воспользуемся функцией:

sbval(v, x1, x2, D, load, score), где

v -                начальное значение искомой величины

x1, x2 –       область поиска решения

D –              функция производных

load –          функция неизвестных начальных условий

score -         функция разницы между вычисленными и заданными значениями

искомой величины

Пример:

В итоге получим:

II этап

Решение полученной задачи

-  зададим вектор начальных условий

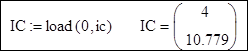
-  зададим количество точек расчета

N:=1500

-  для поиска решения воспользуемся функцией rkfixed()

- 

-  переопределим матрицу найденных значений:

^-  Выделить вектор независимой переменной (t) T:=S^<0>

-  Выделить вектор значений искомой функции (x(t)) X:=S^<1>

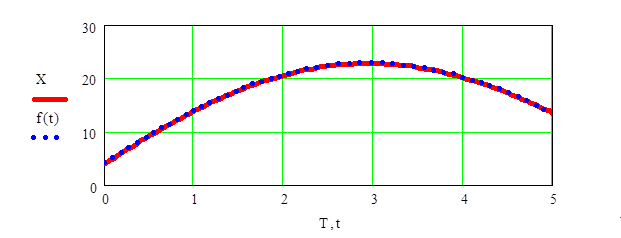
  Построить графики функции X(T) и функции f(x), найденной с помощью функции OdeSolve()

_______________________________________________________________

Задание 3: Найти решение системы ДУ с заданными граничными условиями вышеописанными выше двумя способами и сравнить полученные решения.

y’'=2x+3y,  y(0) =0,  y(1)=1

Индивидуальные задания

Решить представленные граничные задачи двумя способами, сравнить полученные решения.

Замечание: Номер варианта задания выбирается согласно порядковому номеру студента в журнале.

В документе MathCad должны быть указаны постановки задач и номер варианта задания.

Задачи должны быть решены средствами MathCad и сохранены в виде отдельных (трех) документов в индивидуальной папке в каталоге [lab1] следующими  именами

z:\[группа]\[user name].[lab1].[фамилия_1_1.mcd], …[фамилия_1_2.mcd], …[фамилия_1_3.mcd].

Замечание: В случае неправильного именования файлов на диске и не соблюдения вышеуказанных требований лабораторная работа проверяться не будет!