Электротехника \ Теоретические основы электротехники

Расчёт магнитной цепи постоянного тока (с заданным числом витков: W1=500, w3=800). Шифр 821

Страницы работы

19 страниц (Word-файл)

Скачать файл

Содержание работы

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА

Электротехнический факультет

Кафедра «Электротехника»

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №5

по курсу «Теоретические основы электротехники»

Шифр: 821

Выполнил

студент группы ЭС-31

Рубцов К.М.

Проверил

ассистент

Воронин А.В.

2006

Задача №1.

Расчёт магнитной цепи постоянного тока.

На магнитопроводе толщиной h, выполненном из электротехнической стали, размещены намагничивающие обмотки с заданным числом витков (w1=500, w2=600,w3=800). На участках магнитной цепи имеются воздушные зазоры длиной l01, l02 и l03. По обмоткам протекают токи I1, I2, I3.

Пренебрегая потоками рассеяния, определить:

1. Магнитные потоки на всех участках магнитной цепи;

2.Значения магнитной индукции B0 и напряжённости магнитного поля H0 в воздушном зазоре.

Параметры схемы:

H, А/м	B(H), Тл
0.000000	0.000000
96.000000	0.400000
114.000000	0.500000
148.000000	0.600000
192.000000	0.700000
254.000000	0.800000
325.000000	0.900000
414.000000	1.000000
538.000000	1.100000
730.000000	1.200000
1080.000000	1.300000
1940.000000	1.400000
3850.000000	1.500000
6700.000000	1.600000
13000.000000	1.700000
22100.000000	1.800000

1. Определим магнитные потоки на всех участках магнитной цепи.

1.1 Определим вспомогательные геометрические параметры сердечника.

Условные обозначения:
lp[1] - длина осевой линии сегмента левого окна сердечника;
lp[2] - длина осевой линии среднего сегмента сердечника;
lp[3] - длина осевой линии сегмента правого окна.

Sq[1] - площадь поперечного сечения левого сегмента сердечника;
Sq[2] - площадь поперечного сечения среднего сегмента сердечника;
Sq[3] - площадь поперечного сечения правого сегмента сердечника.

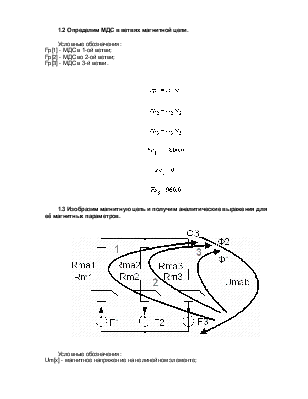
1.2 Определим МДС в ветвях магнитной цепи.

Условные обозначения:
Fp[1] - МДС в 1-ой ветви;
Fp[2] - МДС во 2-ой ветви;
Fp[3] - МДС в 3-й ветви.

1.3 Изобразим магнитную цепь и получим аналитические выражения для её магнитных параметров.

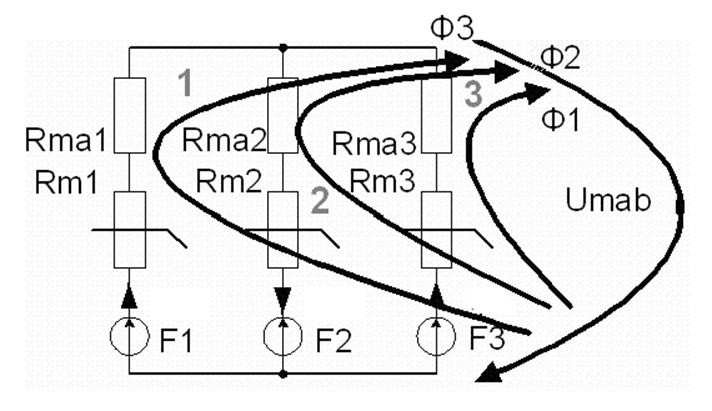
Условные обозначения:
Um[x] - магнитное напряжение на нелинейном элементе;
Uma[x] - магнитное напряжение на линейном элементе;
Umab - магнитное напряжение между двумя узлами цепи.

Линейный элемент в нашем случае представляет собой воздушный промежуток в сегменте сердечника и его магнитное сопротивление и, соответственно, падение магнитного напряжения на нём будут равны нулю, при равенстве нулю его размера:

Составим систему уравнений по законам Кирхгофа и получим аналитические зависимости напряжений на нелинейных элементах (Um[x]) от напряжения между узлами (Umab):

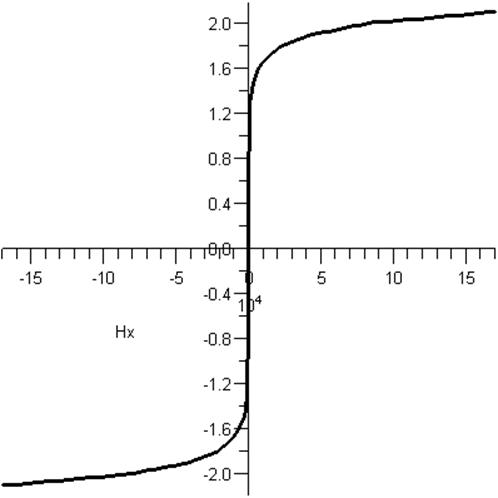
1.4 Заполним таблицу и построим графики.

Для построения графиков величин необходимо перевести таблично заданную функцию B(Н) (индукция по напряжённости магнитного поля) в её аналитический эквивалент. Для этого создадим кусочно заданную функцию с линейно изменяющимися элементами, соединяющими соседние точки (фактически создадим множество отрезков).

Plot

Для табулирования функций (для заполнения таблицы) необходимо выбрать область табулирования и шаг.
Условные обозначения:
Umab_max - модуль обеих границ табулирования (+/-Umab_max);

N - количество шагов табулирования;
D[umab] - шаг табулирования.

Umab_max = sum(abs(Fp[n]), n = 1 .. 3)