1. Исходные данные.
В линейной электрической цепи, содержащей резисторы, катушки индуктивности и конденсаторы, действуют идеальные источники ЭДСek(t)=Ekmsin(ωt+ψk) и тока Jk(t)=Jkmsin(ωt+αk).
Для заданной схемы:
1. Начертить направленный граф схемы, указать на нём дерево и связи.
2. Составить матрицы: узловую А, контурную В и главных сечений Q.
3. Вычислить комплексные сопротивления ветвей.
4. Записать
матрицы действующих значений ЭДС источников ЭДС и токов источников
тока в комплексной форме.
5. Рассчитать на ЭВМ токи в ветвях методом контурных токов.
6. Построить
топографическую векторную диаграмму напряжений для всех элементов
одного из контуров, содержащего 2 или 3 источника ЭДС.
Дано:
R1=50 Ом; L1=0.125 Гн; C1=30 мкФ;
R2=70 Ом; L3=0.115 Гн; C2=25 мкФ;
R4=80 Ом; L5=0.12 Гн; C4=40 мкФ;
R5=60 Ом; L6=0.13 Гн;
R6=55 Ом;
E3M=150
В; ψ3= 250;
E4M=190 В; ψ4= -200;
E6M=210 В; ψ 6= 600;
J1M=3 A; α1=
150;
J4M=6 A; α4=
-150;
J6M= 4 A; α 6= -400.
2. Составим узловую, контурную матрицы, и матрицу главных сечений.
Узловая матрица: 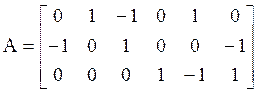 ;
;
Контурная матрица: 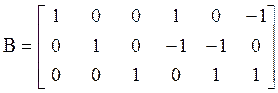 ;
;
Матрица главных сечений: 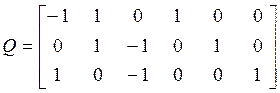 ;
;
3. Вычислим комплексные сопротивления ветвей.
Определим
реактивные сопротивления элементов:
![]() рад;
рад;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
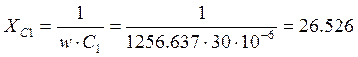 Ом;
Ом;
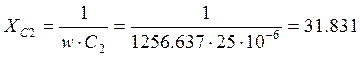 Ом;
Ом;
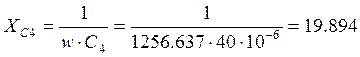 Ом;
Ом;
Находим комплексные сопротивления ветвей:
Z1=R1+j(XL1-XC1)=50+j(157.08-26.526)=50+j130.554=139.801ej69.04
Ом;
Z2=R2-jXC2=70-j31.831=76.897e-j24.45 Ом;
Z3=jXL3=j144.513=144.513ej90
Ом;
Z4=R4-jXC4=80-j19.894=82.436e-j13.97 Ом;
Z5=R5+jXL5=60+j150.796=162.294ej68..3 Ом;
Z6=R6+jXL6=55+j163.363=172.373ej71.39 Ом;
Составим матрицу сопротивлений ветвей.
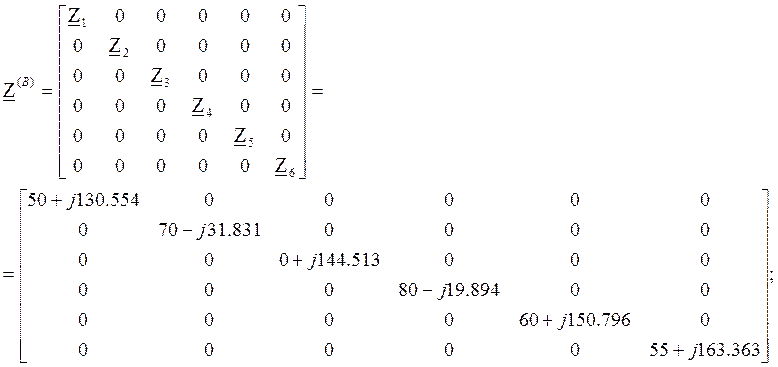
4. Запишем матрицы действующих значений ЭДС
источников ЭДС и токов источников тока в комплексной форме.
Найдём комплексы действующих значений ЭДС и токов
![]()
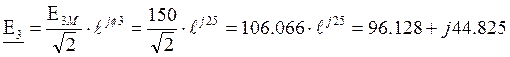 В;
В;
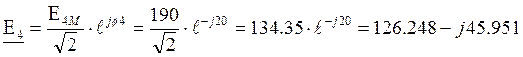 В;
В;
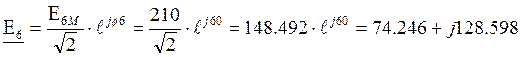 В;
В;
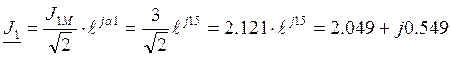 А;
А;
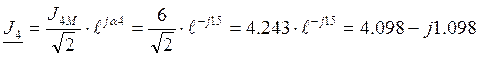 А;
А;
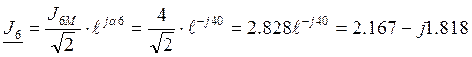 А
А
Составим матрицы действующих значений ЭДС источников ЭДС и токов источников
тока в комплексной форме.
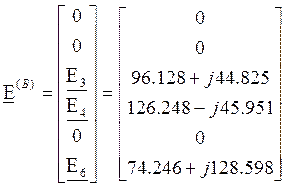 B;
B;
![]()
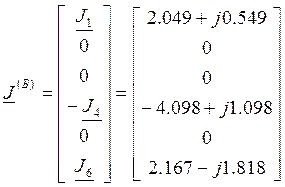 А;
А;
5. Метод контурных токов.
Вычислим матрицу контурных сопротивлений:
![]()
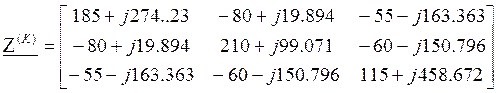 Ом;
Ом;
Вычислим матрицу контурных ЭДС:
![]()
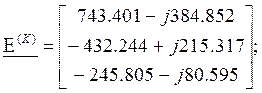 В;
В;
Находим контурные токи:
![]()
![]()
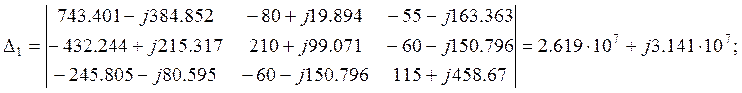
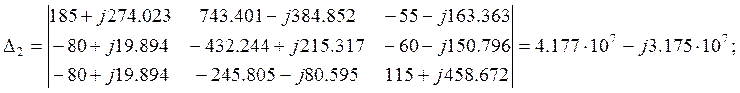
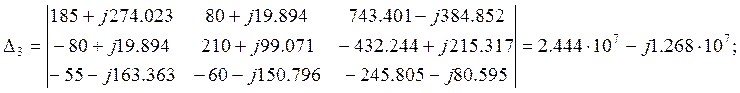
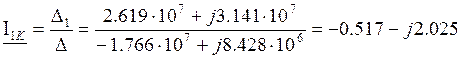 A;
A;
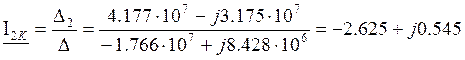 A;
A;
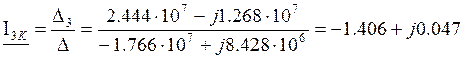 A;
A;
Составим матрицу контурных токов:
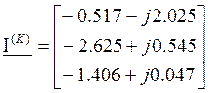 A;
A;
Находим токи в ветвях:
![]()
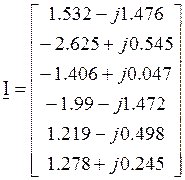 A;
A;
I1= 1.532-j1.476=
2.127e-j43.93
A;
I2= -2.625+j0.545=
2.681ej168.27 A;
I3= -1.406+j0.047
= 1.407ej178.09 A;
I4= -1.99-j1.472
= 2.475e-j143.51
A;
I5= 1.219-j0.498
= 1.317e-j22.22
A;
I6= 1.278+j0.245
= 1.301ej10.85 A;
Запишем мгновенные значения токов в ветвях:
i1(t)=![]() I1sin(ωt+αi1)=3.008sin(1256.637t-43.930); A;
I1sin(ωt+αi1)=3.008sin(1256.637t-43.930); A;
i2(t)=![]() I2sin(ωt+αi2)=3.792sin(1256.637t+168.270); A;
I2sin(ωt+αi2)=3.792sin(1256.637t+168.270); A;
?? i3(t)=![]() I3sin(ωt+αi3)=1.99sin(1256.637t+178.090); A;
I3sin(ωt+αi3)=1.99sin(1256.637t+178.090); A;
i4(t)=![]() I4sin(ωt+αi4)=3.5sin(1256.637t-143.510); A;
I4sin(ωt+αi4)=3.5sin(1256.637t-143.510); A;
i5(t)=![]() I5sin(ωt+αi5)=1.863sin(1256.637t-22.220); A; i6(t)=
I5sin(ωt+αi5)=1.863sin(1256.637t-22.220); A; i6(t)=![]() I6sin(ωt+αi6)=1.84sin(1256.637t+10.850); A;
I6sin(ωt+αi6)=1.84sin(1256.637t+10.850); A;
Баланс мощностей:
По закону Ома найдем напряжение на источниках тока.
![]() B;
B;
![]()
![]()
Находим полную мощность источников,
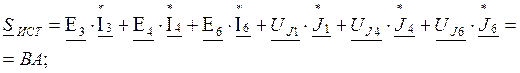
Находим мощность приемников.
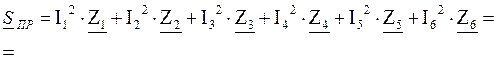
6. Построим топографическую векторную диаграмму напряжений всех элементов контура a-b-c-d-e-f-g-h-l.
φa=0 B;
φb= φa-I4·R4=0-(-1.99-j1.472)
·80=159.2+j117.76 B;
φc = φb-I1·(-jXC1)=(159.2+j117.76)-(1.532-j1.476)
·(-26.526)=198.352+j158.398 B;
φd= φc-I1 ·R1=(198.352+j158.398)-(1.532-j1.476)
·50=121.752+j232.198 B;
φe= φd-I1 ·(jXL1)=
(121.752+j232.198)-(1.532-j1.476) ·(j157.08)= -110.097-j8.448 B;
φf= φe+I6 ·(jXL6)=(
-110.097-j8.448)+(1.278+j0.245) ·(j163.363)= -151.592+200.166 B;
φg= φf-E6=(-151.592+200.166)-(74.246+j128.598)=
-225.838+j71.568 B;
φh= φg+I6 ·R6=(-225.838+j71.568)+(
1.278+j0.245) ·55= -155.603+j85.538 B;
φl= φh-I4 ·(-jXC4)=(
-155.603+j85.538)-(-1.99-j1.472) ·(-j19.894)= -126.318+j45.948 B;
φa= φl+E4=(-126.318+j45.948)+(126.248-j45.951)=
-0.07-j0.003 ≈ 0 B;
Топографическая векторная диаграмма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.