БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА
кафедра «Электротехника»
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №4
по курсу «Теоретические основы электротехники»
Шифр: 128
|
Выполнил: ст. гр. ЭС-21 Рубцов К.М. |
Проверил: преподаватель Воронин А.В. |
2006
Задание 1.
В цепи с источником постоянной ЭДС происходит коммутация.
Для данной схемы:
1. Классическим методом определить закон изменения во времени токов
всех ветвей схемы и напряжений на катушке ![]() и
конденсаторе
и
конденсаторе ![]() .
.
2. Построить графики изменения во времени тока в катушке ![]() и напряжения на катушке
и напряжения на катушке ![]() .
.
3. Операторным методом найти закон изменения во времени тока переходного
процесса в катушке ![]() или напряжения на конденсаторе
или напряжения на конденсаторе ![]() .
.
Исходные данные:
E = 40 В; L = 125 мГн; C = 55 мкФ;
r1 = 16 Ом; r2 = 17 Ом; r3 = 14 Ом; r4 = 12 Ом;
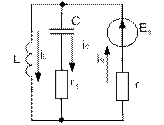
Исходная схема:
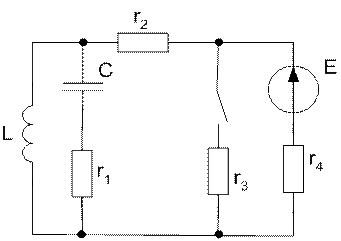
1.
Классическим методом определить закон изменения во времени токов всех ветвей схемы
и напряжений на катушке ![]() и конденсаторе
и конденсаторе ![]() .
.
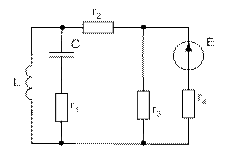
Прежде всего, преобразуем расчетную схему, которая получится после замыкания рубильника к более удобному для расчета виду. Для этого объединим ветвь с сопротивлением r3 и ветвь с сопротивлением r4 и ЭДС Е, а так же преобразуем r2.
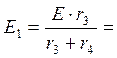 21.538В;
21.538В;
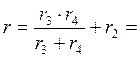 23.462Ом;
23.462Ом;
После коммутации в схеме будут
протекать переходные токи ![]() ,
, ![]() ,
, ![]() . Для
расчета этой цепи составим уравнения по законам Кирхгофа:
. Для
расчета этой цепи составим уравнения по законам Кирхгофа:
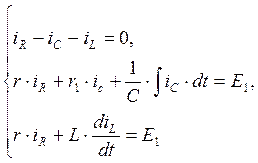
1. Найдем корни системы характеристических уравнений.
Произведем замену дифференцирования умножением на оператор p, а интегрирования – делением на этот же оператор, что позволяет получить систему алгебраических характеристических уравнений. Запишем эту систему для свободных составляющих переходных токов тогда:
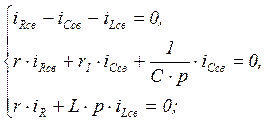
Решение этой системы будет найдено, если определитель системы будет равен нулю. Таким образом, получаем:
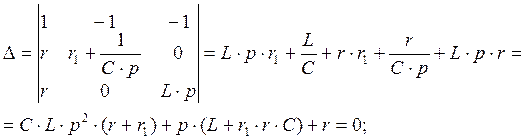
Найдем корни, полученного квадратного уравнения:
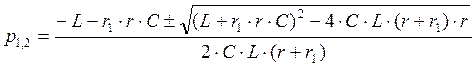 ;
;
Подставляя числовые значения, получим:
![]() -319.619+59.499j
-319.619+59.499j ![]()
![]() -319.619-59.499j
-319.619-59.499j ![]()
2. Определим принужденные составляющие тока и напряжения.
Определим принужденные составляющие тока и напряжения из схемы:
Из схемы, получаем:
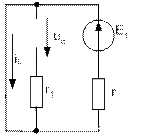
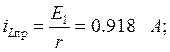
![]()
3. Определим независимые начальные условия.
Определим независимые начальные условия из схемы:
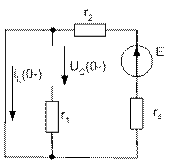
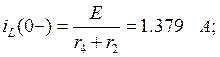
![]()
Из законов коммутации следует, что в момент замыкания:
![]()
![]()
4. Определим зависимые начальные условия.
Определим зависимые начальные условия из схемы:
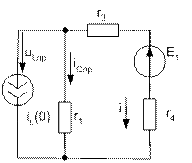
Рассмотрим контур:
![]()
Найдем контурный ток i:
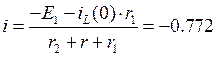 А;
А;
Тогда ток на конденсаторе равен:
![]() ;
;
Найдем напряжение на катушке:
![]()
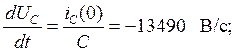
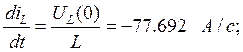
5. Определим постоянные интегрирования.
Определим
постоянные интегрирования для тока ![]() :
:
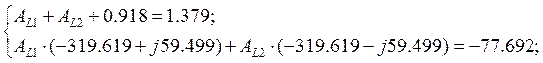
Решая,
систему уравнений найдем ![]() и
и ![]()
![]()
![]()
Определим
постоянные интегрирования для напряжения ![]() :
:
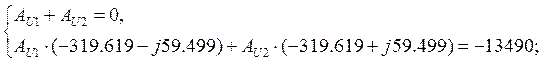
![]()
![]()
5.
Определим закон изменения во времени всех токов и напряжений ![]() и
и![]() .
.
Закон ![]() будет
равен:
будет
равен:

Закон ![]() будет
равен:
будет
равен:
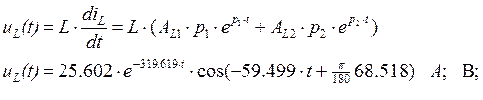
Закон ![]() будет
равен:
будет
равен:
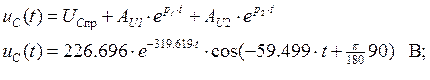
Закон ![]() будет
равен:
будет
равен:
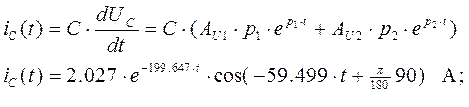
Закон ![]() будет
равен:
будет
равен:
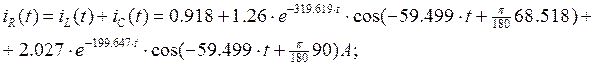
Закон ![]() будет
равен
будет
равен![]() :
:
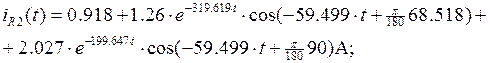
Закон ![]() будет
равен
будет
равен 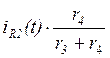 :
:
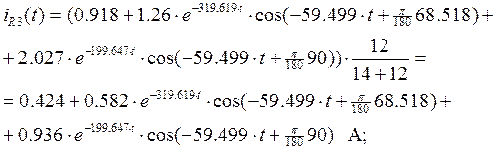
Закон ![]() будет равен
будет равен
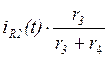 :
:
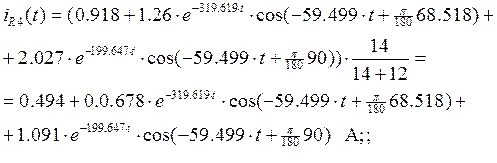
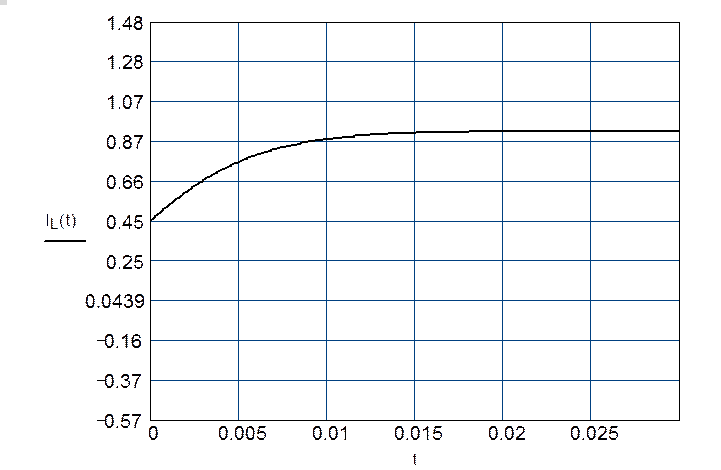
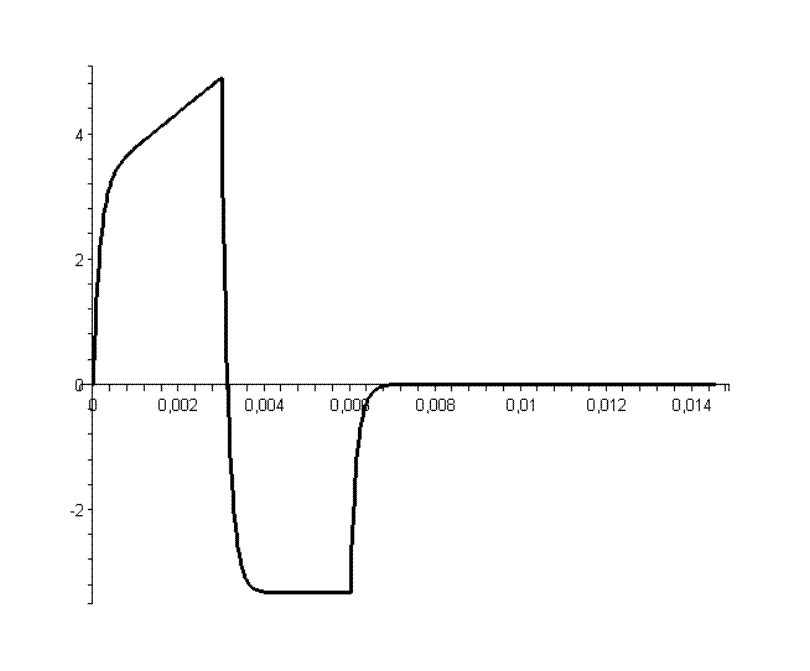
2. Построить
графики изменения во времени тока в катушке ![]() и напряжения
на катушке
и напряжения
на катушке ![]() .
.
|
|
|
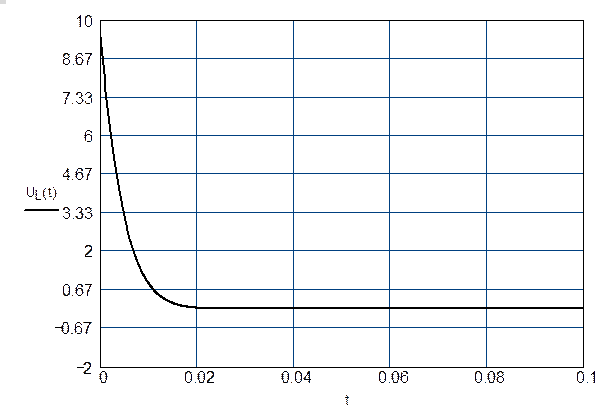
График изменения напряжения на катушке
|
|
3. Операторным методом найти
закон изменения во времени тока переходного процесса в катушке ![]() или напряжения на конденсаторе
или напряжения на конденсаторе ![]() .
.
1. Определим независимые начальные условия:
Определяем независимые начальные условия:

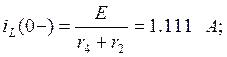
![]()
Из законов коммутации следует, что в момент замыкания:
![]()
![]()
2. Определим ток на катушке:
Произведем операторную замену элементов, тогда наша схема будет выглядеть:
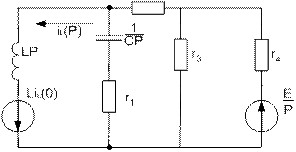
Произведем эквивалентные преобразования:
1. Объединим ветви 4-ую, 3-ею и 2-ую:
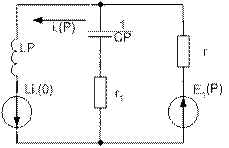
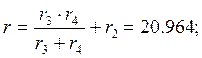
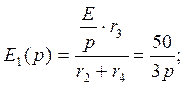
2. Объединим ветви с сопротивлением  :
:
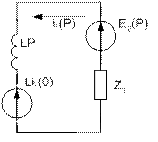
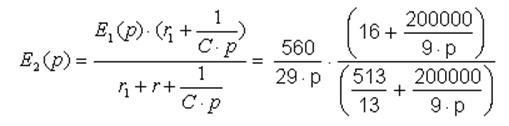
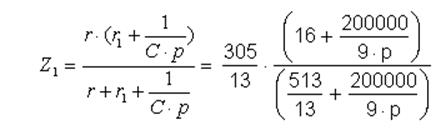
Тогда ![]() и
и ![]() будут равны соответственно:
будут равны соответственно:
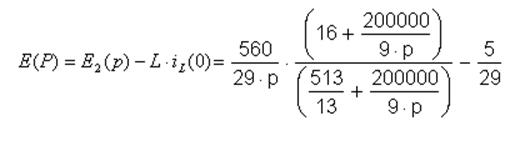
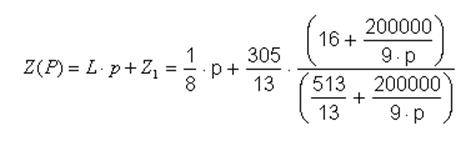
Найдем ток на катушке:
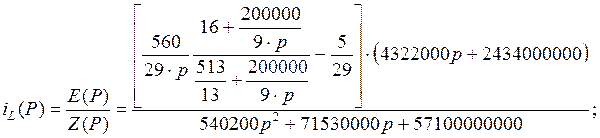
Решим уравнение:
![]()
Корни этого уравнения будут равны:
![]() -66.207+318.305j
-66.207+318.305j ![]()
![]() -66.207-318.305j
-66.207-318.305j ![]()
Найдем закон изменения тока ![]() :
:
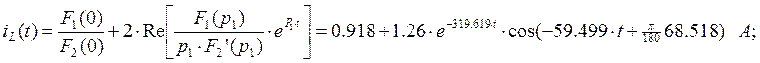
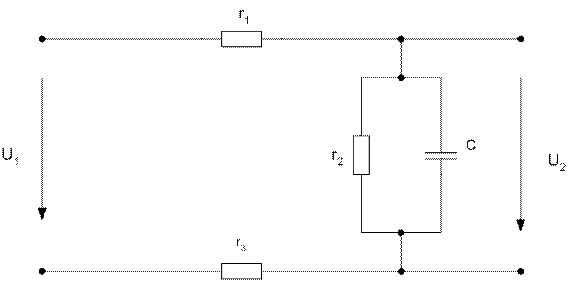
Задача №2
На вход несимметричного чётырёхполюсника подаётся импульс напряжения u1(t) длительностью t0. Значения параметров элементов схемы четырёхполюсника и параметров импульса приведены в таблицы. Определить закон изменения во времени напряжения u2(t) и построить в масштабе его график. Задачу решить с помощью интеграла Дюамеля.
|
r1 , Ом |
r2 , Ом |
r3 , Ом |
L, мГн |
С, мкФ |
U0 , В |
t0 , мс |
|
8 |
6 |
4 |
- |
40 |
10 |
6 |
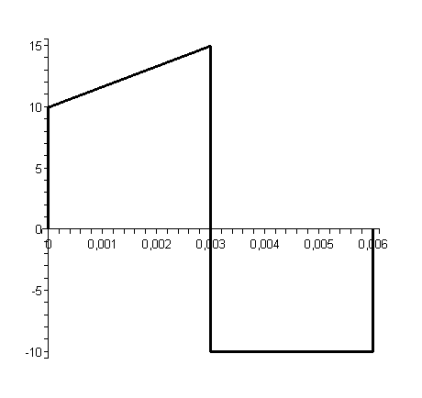
|
|
|
Для определения переходной функции для напряжения на выходе четырёхполюсника h(t), напряжение на которой и является напряжением на конденсаторе:
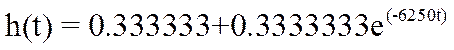
Запишем выражение h(t-τ) путём формальной замены t на (t-τ): τ – переменная интегрирования; t – момент времени выходного напряжения:
h(t-τ)= ![]()
Найдём аналитическое выражение для функции входного импульса:
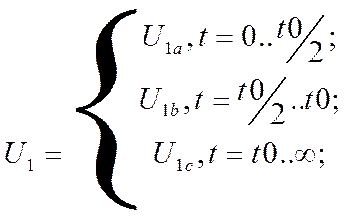
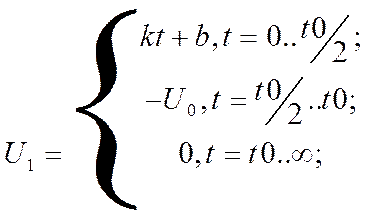
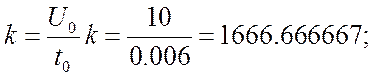
С помощью интеграла Дюамеля определим функцию напряжение на выходе четырёхполюсника:
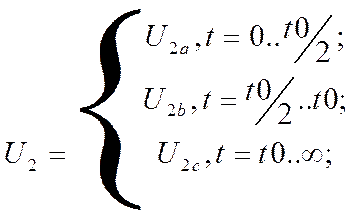
Запишем выражение h(t-τ), h(t-t0/2), h(t-t0) путём формальной замены t на (t-τ), (t-t0/2) ,(t-t0):
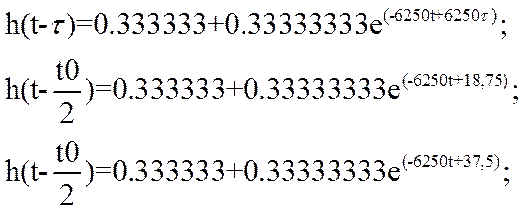
|
|
|
В итоге получим функцию:
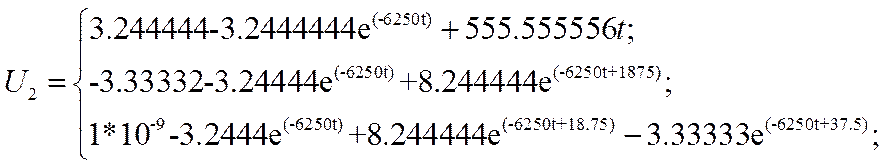
Построим гпафик функции напряжения на
выходе четырёхполюсника:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.