БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА
Электротехнический факультет
Кафедра «Электротехника»
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №4
по курсу «Теоретические основы электротехники»
Шифр: 863
|
Выполнил студент группы ЭС-21 Матылицкий И. В. |
Проверил ассистент Воронин А.В. |
2006
Задача №1.
В цепи с источником постоянной ЭДС происходит комутация.
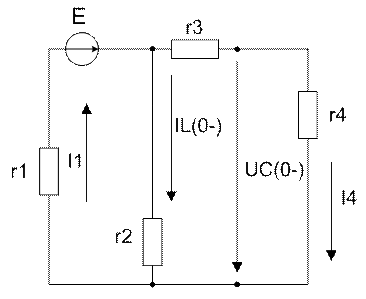
Для заданной схемы:
1. Классическим методом определить закон изменения во времени токов всех ветвей схемы и напряжений на катушке uL(t) и конденсаторе uc(t).
2. Построить графики изменения во времени тока в катушке iL(t) и напряжения на её зажимах uL(t).
3. Операторным методом найти закон изменения во времени тока переходного процесса в катушке iL(t) или напряжения на конденсаторе uc(t).
Исходные данные.
|
E, В |
L, мГн |
C, мкФ |
r1, Ом |
r2, Ом |
r3, Ом |
r4, Ом |
|
35 |
110 |
65 |
22 |
17 |
15 |
19 |
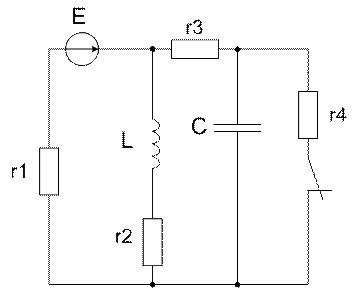
Определим классическим методом закон изменения во времени токов всех ветвей схемы и напряжений на катушке uL(t) и конденсаторе uc(t).
Примечание.
iL(0-)=iLpre ; UC(0-)=UCpre ;
iL(0+)=iLsuc ; UC(0+)=UCsuc ;
Es=E;
in(0+)=isucn;
UL(0+)= ULsuc.
inпр=ipstn.
UCпр=UCpst.
Запишем систему дифференциальных уравнений по 1-му и 2-му законам Кирхгофа для схемы при коммутации:
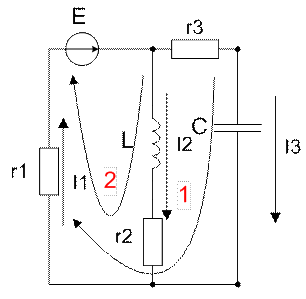
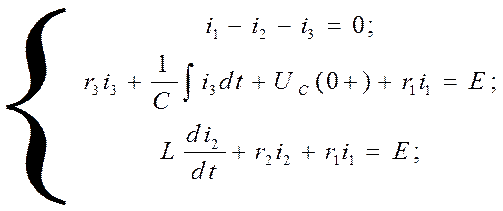
Принимая во внимание, что:
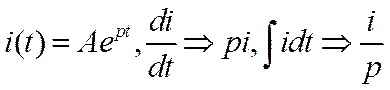
алгебраизируем данную систему следующим образом:
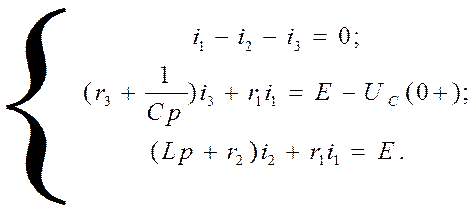
Найдём её определитель, учитывая, что i1, i2, i3– искомые функции (относительно чего эта система решается):
![Delta := Matrix([[1, -1, -1], [22, 0, 15+200000/13/p], [22, .11*p+17, 0]])](https://files3.vunivere.ru/workbase/00/03/71/12/images/image006.jpg)
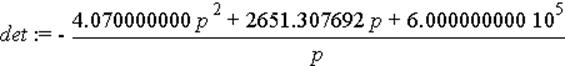
Решаем параметрическое уравнение данной системы:
![]()
Находим корни:
![]()
Получено два комплексно-сопряжённых корня.
Найдём ток в катушке (iL(0-)) и напряжение на конденсаторе (UL(0-)) до коммутации:
![Ro[0] := r[1]+r[2]*(r[3]+r[4])/(r[2]+r[3]+r[4])](https://files3.vunivere.ru/workbase/00/03/71/12/images/image011.jpg) ;
; ![Ro[1] := r[2]*(r[3]+r[4])/(r[2]+r[3]+r[4])](https://files3.vunivere.ru/workbase/00/03/71/12/images/image012.jpg) ;
;
![i[Lpre] := Es*Ro[1]/(Ro[0]*r[2])](https://files3.vunivere.ru/workbase/00/03/71/12/images/image013.jpg) ;
; ![U[Cpre] := Es*Ro[1]*r[4]/(Ro[0]*(r[3]+r[4]))](https://files3.vunivere.ru/workbase/00/03/71/12/images/image014.jpg) ;
;
![]() А ;
А ; ![]() В.
В.
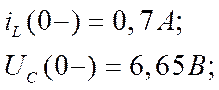
Согласно закону коммутации:
iL(0-)= iL(0+) ; UC(0-)=UC(0+),
где iL(0+) – ток в катушке сразу после коммутации; UC(0+) – напряжение на конденсаторе сразу после коммутации.
![]() А;
А;
![]() В;
В;
Цепь сразу после момента коммутации:
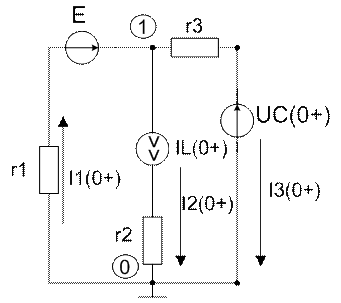
Рассчитаем цепь с помощью метода узловых потенциалов:
![phis := solve(phi[1]*(1/r[1]+1/r[3]) = Es/r[1]-i[Lsuc]+U[Csuc]/r[3], phi[1])](https://files3.vunivere.ru/workbase/00/03/71/12/images/image022.jpg)
![]() В;
В;
![i[suc1] := (phi[0]-phi[1]+Es)/r[1]](https://files3.vunivere.ru/workbase/00/03/71/12/images/image024.jpg) ;
; ![i[suc3] := (phi[1]-phi[0]-U[Csuc])/r[3]](https://files3.vunivere.ru/workbase/00/03/71/12/images/image025.jpg) ;
;
![]() .
.
![]()
![]() А;
А; ![]() А;
А;
![]() А;
А;
![]() В;
В; ![]() В;
В;
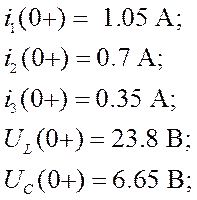
Выразим производные искомых токов и напряжений:
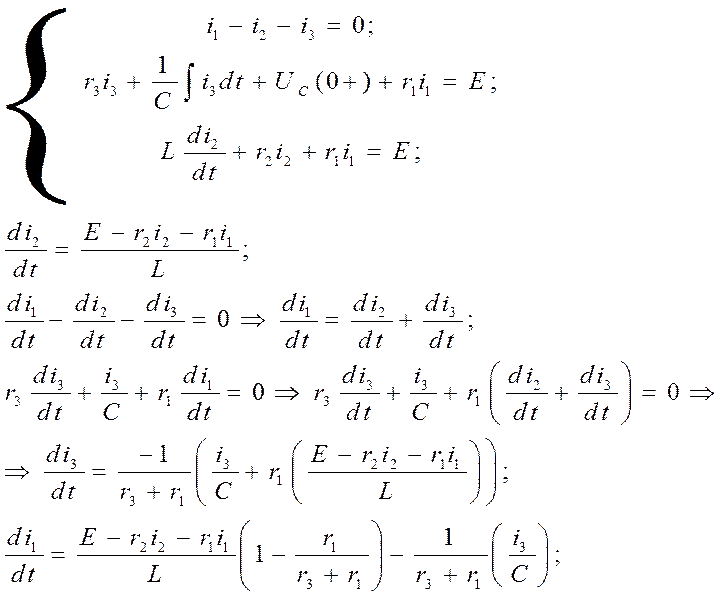
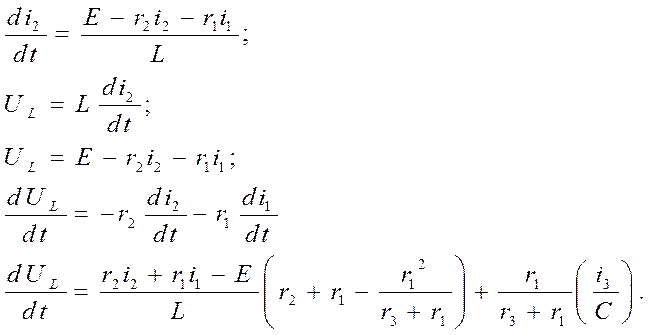
В результате получим:
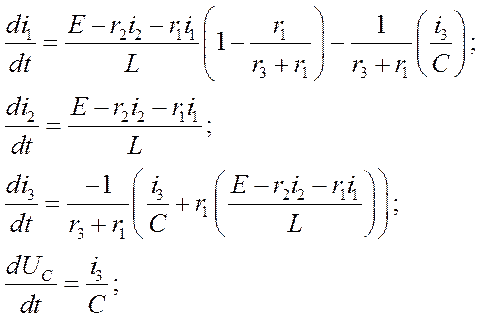
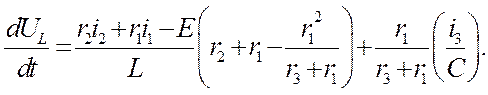
Рассчитаем состояние схемы после коммутации при окончании переходного процесса (принуждённый режим):
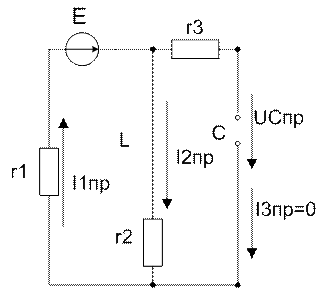
![i[pst1] := Es/(r[1]+r[2])](https://files3.vunivere.ru/workbase/00/03/71/12/images/image038.jpg)
![]()
![]()
![]()
![]() А;
А; ![]() А;
А; ![]() А;
А;
![]() В;
В; ![]() В;
В;
В результате получим:
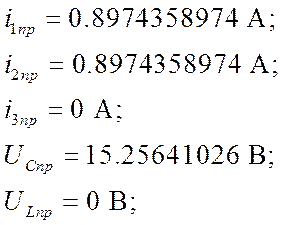
Запишем выражения функций токов и напряжений с учётом параметра p и найденных принуждённых значений:
![i[1] := proc (t) options operator, arrow; i[pst1]+A[1]*exp(Re(p[1])*t)*sin(abs(Im(p[1]))*t+phi[1]) end proc](https://files3.vunivere.ru/workbase/00/03/71/12/images/image048.jpg)
![i[2] := proc (t) options operator, arrow; i[pst2]+A[2]*exp(Re(p[1])*t)*sin(abs(Im(p[1]))*t+phi[2]) end proc](https://files3.vunivere.ru/workbase/00/03/71/12/images/image049.jpg)
![i[3] := proc (t) options operator, arrow; i[pst3]+A[3]*exp(Re(p[1])*t)*sin(abs(Im(p[1]))*t+phi[3]) end proc](https://files3.vunivere.ru/workbase/00/03/71/12/images/image050.jpg)
![U[L] := proc (t) options operator, arrow; U[Lpst]+A[4]*exp(Re(p[1])*t)*sin(abs(Im(p[1]))*t+phi[4]) end proc](https://files3.vunivere.ru/workbase/00/03/71/12/images/image051.jpg)
![U[C] := proc (t) options operator, arrow; U[Cpst]+A[5]*exp(Re(p[1])*t)*sin(abs(Im(p[1]))*t+phi[5]) end proc](https://files3.vunivere.ru/workbase/00/03/71/12/images/image052.jpg)
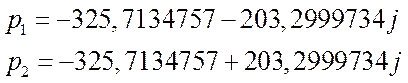
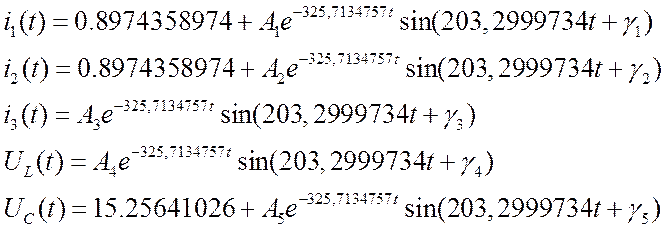
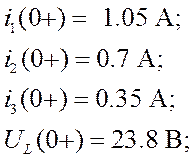
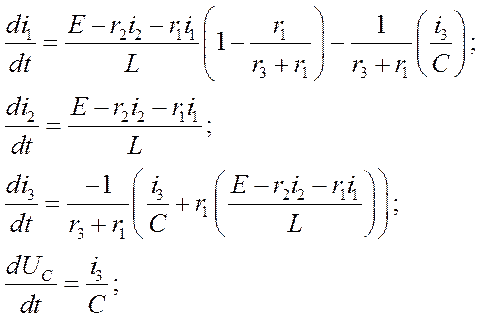
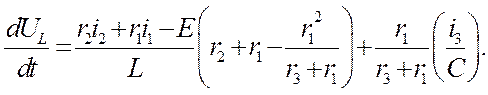
Найдём неизвестные параметры функций с помощью решения следующих систем уравнений. Для этого условимся, что t=0+ (непосредственно после коммутации):
![curs[1] := {i[1](0) = i[suc1], (Es-r[2]*i[suc2]-r[1]*i[suc1])*(1-r[1]/(r[3]+r[1]))/Lk-i[suc3]/((r[3]+r[1])*Ck) = id[1]}](https://files3.vunivere.ru/workbase/00/03/71/12/images/image056.jpg)
![curs[2] := {i[2](0) = i[suc2], (Es-r[2]*i[suc2]-r[1]*i[suc1])/Lk = id[2]}](https://files3.vunivere.ru/workbase/00/03/71/12/images/image057.jpg)
![curs[3] := {i[3](0) = i[suc3], -(i[suc3]/Ck+r[1]*(Es-r[2]*i[suc2]-r[1]*i[suc1])/Lk)/(r[3]+r[1]) = id[3]}](https://files3.vunivere.ru/workbase/00/03/71/12/images/image058.jpg)
![vols[L] := {U[Lsuc] = U[L](0), (r[2]*i[suc2]+r[1]*i[suc1]-Es)*(r[2]+r[1]-r[1]^2/(r[3]+r[1]))/Lk+r[1]*i[suc3]/((r[3]+r[1])*Ck) = Ud[L]}](https://files3.vunivere.ru/workbase/00/03/71/12/images/image059.jpg)
![vols[C] := {U[Csuc] = U[C](0), i[suc3]/Ck = Ud[C]}](https://files3.vunivere.ru/workbase/00/03/71/12/images/image060.jpg) ,
,
где Xdn – производная функции Xn в точке t=0+:
![]()
![]()
![]()
![]()
![]()
Системы уравнений составлены по общей схеме:
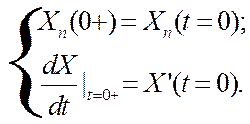
Перепишем их в числовой форме:
![]()
![]()
![]()
![]()
![]()
Найдём корни этих уравнений:
![]()
![]()
![]()
![]()
![]()
Перепишем функции токов и напряжений в соответствии с найденными корнями (берутся корни с An>0):
![]()
![]()
![i[3] := .3828235608*exp(-325.7134757*t)*sin(203.2999734*t+1.987916830)](https://files3.vunivere.ru/workbase/00/03/71/12/images/image079.jpg)
![]()
![]()
Построим графики изменения во времени тока в катушке iL(t) и напряжения на её зажимах uL(t).
График изменения во времени тока в катушке (iL(t)= i2(t)):
![[Plot]](https://files3.vunivere.ru/workbase/00/03/71/12/images/image082.gif)
График изменения во времени напряжения на зажимах катушки uL(t):
![[Plot]](https://files3.vunivere.ru/workbase/00/03/71/12/images/image083.jpg)
Операторным методом найдём закон изменения во времени напряжения на конденсаторе uc(t).
Независимые начальные условия:
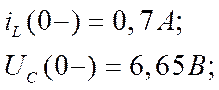
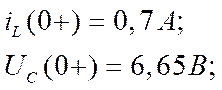
Составим операторную схему замещения цепи:
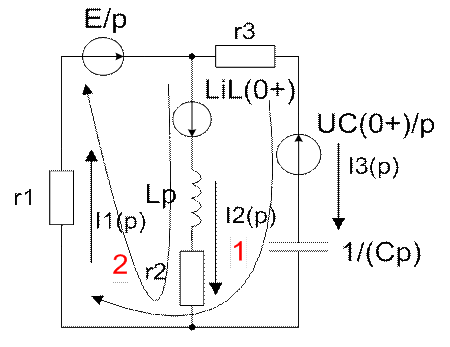
Запишем уравнения Кирхгофа для обозначенных контуров и токов:
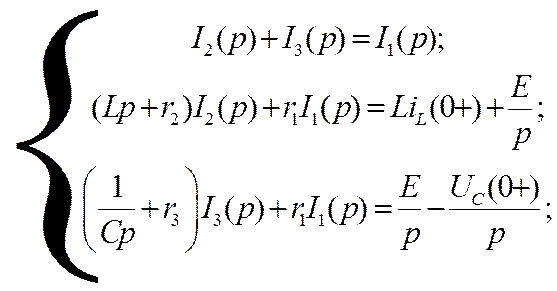
Перепишем в численном виде и решим систему относительно образов токов:
![ks := {Ip[2]+Ip[3] = Ip[1], (.11*p+17)*Ip[2]+22*Ip[1] = 0.7700000000e-1+35/p, (200000/13/p+15)*Ip[3]+22*Ip[1] = 28.35000000/p}](https://files3.vunivere.ru/workbase/00/03/71/12/images/image086.jpg)
Решение системы:
![kssi := {Ip[1] = .3500000000*(2000000000.+8140100.*p+15873.*p^2)/(p*(5291.*p^2+3446700.*p+780000000.)), Ip[2] = .7000000000*(3446700.*p+5291.*p^2+1000000000.)/(p*(5291.*p^2+3446700.*p+780000000.)), Ip...](https://files3.vunivere.ru/workbase/00/03/71/12/images/image087.jpg)
![kssi := [Ip[1] = .3500000000*(2000000000.+8140100.*p+15873.*p^2)/(p*(5291.*p^2+3446700.*p+780000000.)), Ip[2] = .7000000000*(3446700.*p+5291.*p^2+1000000000.)/(p*(5291.*p^2+3446700.*p+780000000.)), Ip...](https://files3.vunivere.ru/workbase/00/03/71/12/images/image088.jpg)
Выразим следующим образом напряжение на конденсаторе:
![Up[C] := U[Csuc]/p+Ip[3]/(Ck*p)](https://files3.vunivere.ru/workbase/00/03/71/12/images/image089.jpg)
![Up[C] := .3500000000*(100529.*p^2+146887300.*p+0.3400000000e11)/(p*(5291.*p^2+3446700.*p+780000000.))](https://files3.vunivere.ru/workbase/00/03/71/12/images/image090.jpg)
Определим две функции-образа следующим образом:
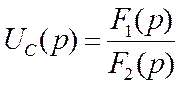
![]()
![]()
Найдём параметр p процесса через уравнение:
![]()
В результате получаем следующие решения:
![]()
Найдём через лаплас-образ функции напряжения на конденсаторе саму функцию следующим образом:
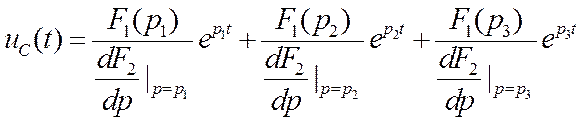
В результате развёртки экспоненциальных функций и упрощения получим:
![]()
Численные отличия функций, полученных при классическом и операторном методе расчёта:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача №2
На вход несимметричного чётырёхполюсника подаётся импульс напряжения u1(t) длительностью t0. Значения параметров элементов схемы четырёхполюсника и параметров импульса приведены в таблицы. Определить закон изменения во времени напряжения u2(t) и построить в масштабе его график. Задачу решить с помощью интеграла Дюамеля.
|
r1 ,Ом |
r2 , Ом |
r3 , Ом |
L,мГн |
С, мкФ |
U0 ,В |
t0 ,мс |
|
8 |
4 |
6 |
22 |
55 |
18 |
8 |
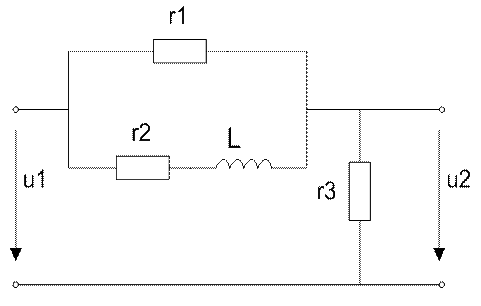
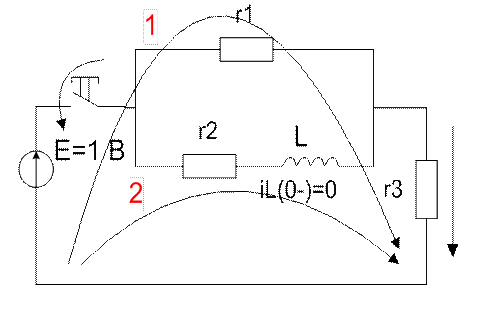
Определим переходную функцию h(t) для выходных зажимов исследуемой цепи. (Переходная функция – зависимость напряжения на выходе схемы от времени при подаче на вход схемы единичного напряжения. Понятие переходной функции как и весь способ применимо только к схемам с нулевыми независимыми начальными условиями.)
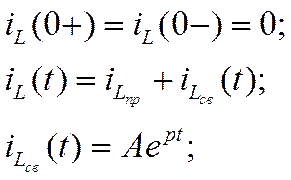
|
|
|
Для определения переходной функции для напряжения на выходе четырёхполюсника h(t) необходимо знать ток i3 3-й ветви, напряжение на которой и является напряжением на выходе. Для этого запишем по законам Кирхгофа и решим систему относительно токов i1 , i3:
![ks := {i[1]+i[L] = i[3], r[2]*i[L]+Lk*(diff(i[L], t))+r[3]*i[3] = Es1}](https://files3.vunivere.ru/workbase/00/03/71/12/images/image150.jpg)
![]()
![]()
После умножения полученного выражения для тока i3 на r3 получим следующее выражение для h(t) :
h(t)=![]()
Запишем выражение h(t-τ) путём формальной замены t на (t-τ): τ – переменная интегрирования; t – момент времени выходного напряжения:
h(t-τ)= ![]()
Найдём аналитическое выражение для функции входного импульса:
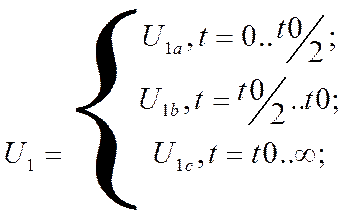
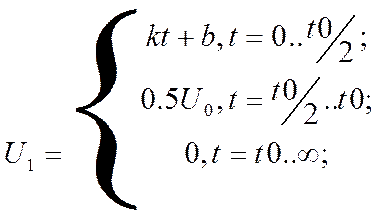
![]()
![]()
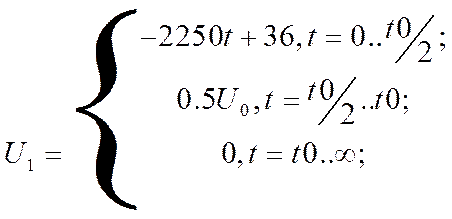
С помощью интеграла Дюамеля определим функцию напряжение на выходе четырёхполюсника:
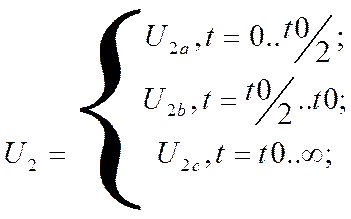
|
|
|
В итоге получим функцию:
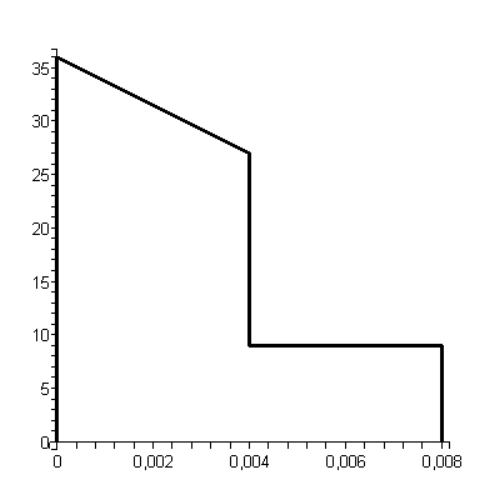
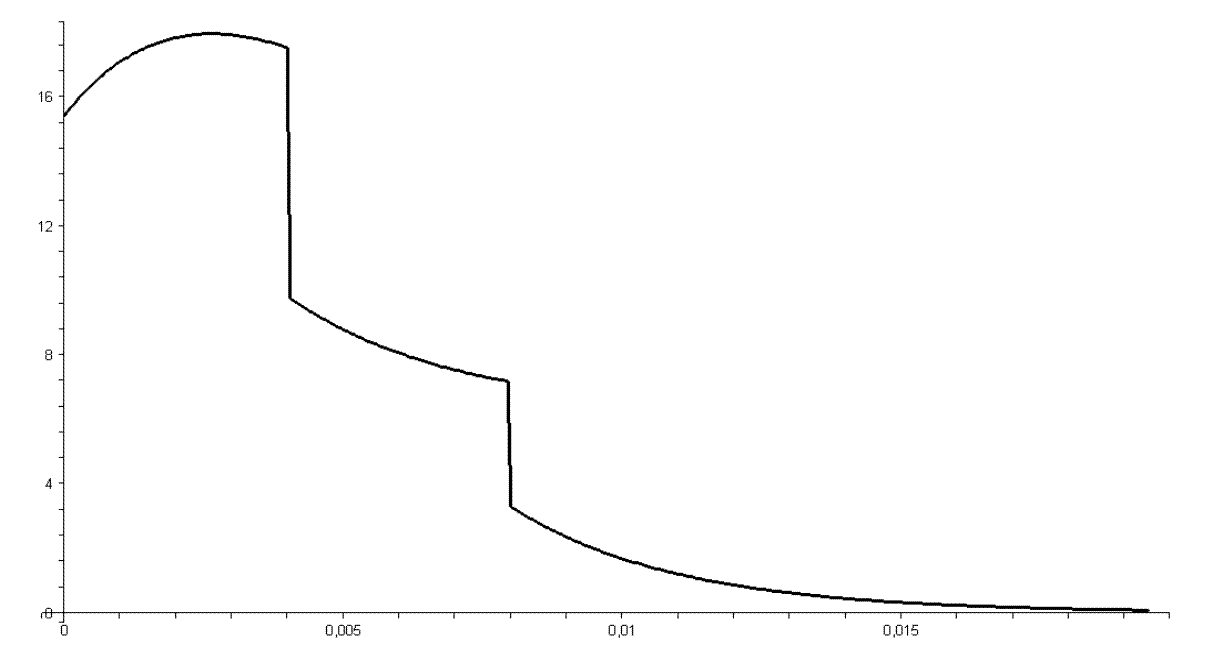
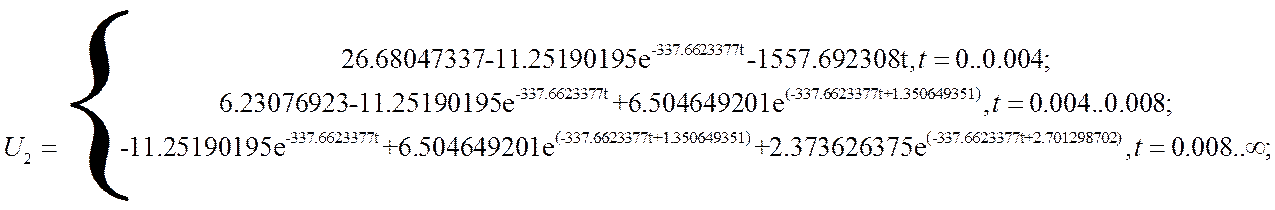 Построим гпафик функции напряжения на
выходе четырёхполюсника:
Построим гпафик функции напряжения на
выходе четырёхполюсника:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.