БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА
Кафедра “Электротехника”
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1
По курсу “Теория линейных электрических цепей”
Шифр 208
Выполнил: Проверил:
ст. гр. ЭМ-31 ассистент
Мирончик И.П. Грапов А.В.
2003
Задание на первую задачу расчетно-графической работы №1:
РАСЧЕТ ДВУХПОЛЮСНИКОВ
1.1 Схему заданного двухполюсника привести к канонической форме, параметры элементов схемы рассчитать (привести вывод коэффициентов необходимых для расчета параметров элементов эквивалентного двухполюсника).
1.2 Построить схему и рассчитать параметры элементов двухполюсника обратного приведенному.
1.3 Определить все резонансные частоты и характеры резонансов обоих двухполюсников. Построить характеристические строки с расположенными на них нулями и полюсами функции для обоих двухполюсников.
1.4 Составить выражение частотной характеристики входного сопротивления в канонической форме для обоих двухполюсников.
1.5 Рассчитать и построить частотные характеристики входных сопротивлений обоих двухполюсников.
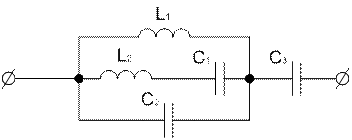
Рисунок 1.1 – Схема исходного двухполюсника
Исходные данные:
L1=23 мГн; C1=1.3 мкФ; R=700 Ом;
L2=16 мГн; C2=1.6 мкФ; C3=1.9 мкФ;
1.1 Схему заданного двухполюсника привести к канонической форме. Параметры элементов схемы рассчитать (привести вывод коэффициентов необходимых для расчета параметров элементов эквивалентного двухполюсника).
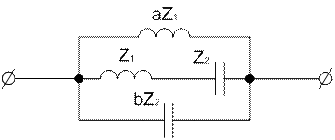
Рисунок 1.2 – Часть преобразуемой схемы
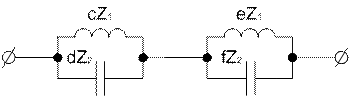
Рисунок 1.3 – Эквивалентная замена преобразуемой схемы
Для нахождения коэффициентов преобразования составим уравнения сопротивлений обоих двухполюсников.
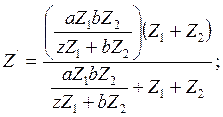
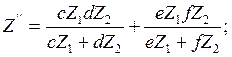
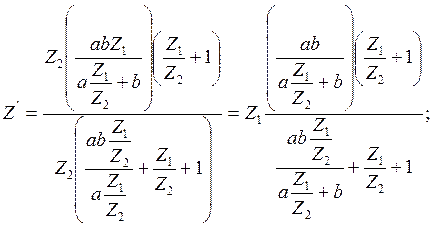
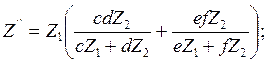
Рассчитаем коэффициенты преобразования:
Пусть частота ![]() ,
тогда:
,
тогда:
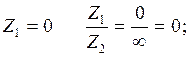
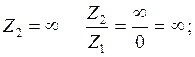
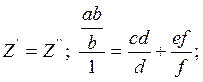
Таким образом ![]() (1)
(1)
Пусть частота ![]() ,
тогда:
,
тогда:
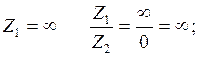
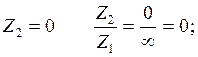
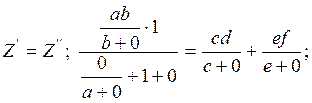
Следовательно ![]() (2)
(2)
Пусть частота ![]() ,
при которой
,
при которой 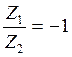 :
:
![]() , если
, если 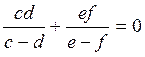 ; (3)
; (3)
При 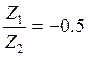 получим:
получим:
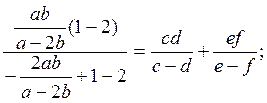
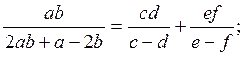 (4)
(4)
Выразим коэффициенты a и b:
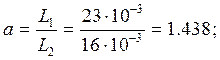
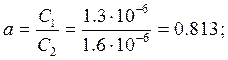
Решая систему уравнений (1), (2), (3) и (4) получим следующие значения коэффициентов:
c= 0.232; d= 0.49; e= 1.205; f= 0.323;
Из найденных коэффициентов выразим неизвестные номиналы элементов эквивалентного двухполюсника:
![]() ;
;
![]() ;
;
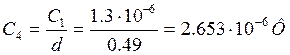 ;
;
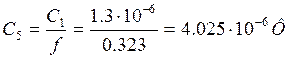 ;
;
1.2 Построить схему и рассчитать параметры элементов двухполюсника, обратного приведенному.
Для построения обратного двухполюсника сделаем следующее:
1 Все реактивные элементы двухполюсника заменяем на дуальные;
2 Все схемы соединений исходного двухполюсника заменяем на дуальные.
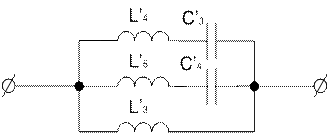
Рисунок 1.5 – Обратный двухполюсник
Рассчитаем его элементы:
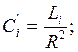
![]()
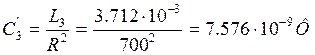 ;
;
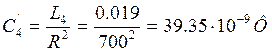 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
1.3 Определить все резонансные частоты и характеры резонансов обоих двухполюсников. Построить характеристические строки с расположенными на них нулями и полюсами функции для обоих двухполюсников.
Определим все резонансные частоты и характеры резонансов исходного двухполюсника. Для этого запишем входное сопротивление канонического двухполюсника.
Первым наступит резонанс напряжений, т.к. нет пути прохождения постоянному току.
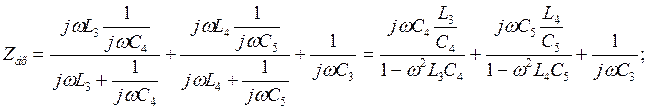
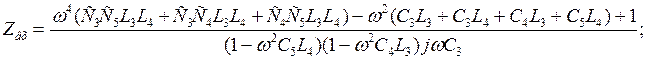
Найдем нули функции:
![]()
Решая данное биквадратное уравнение получим:
![]()
![]()
Найдем полюсы функции:
![]()
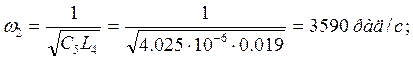
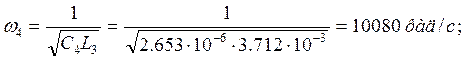
Определим все резонансные частоты и характеры резонансов обратного двухполюсника:
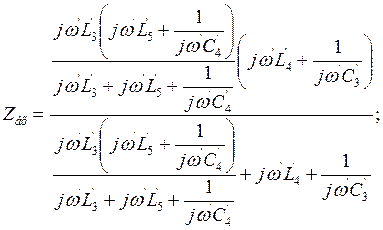
![]()
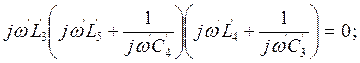
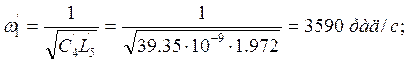
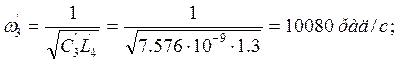
![]()
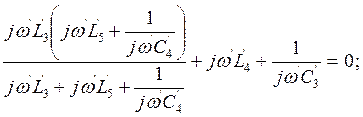
Преобразуя это выражение получим следующее биквадратное уравнение:
![]()
Решая данное биквадратное уравнение получим:
![]()
![]()
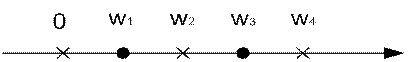
Рисунок 1.5 – Характеристическая строка исходного двухполюсника
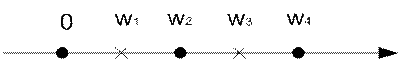
Рисунок 1.6 – Характеристическая строка обратного двухполюсника
1.4 Составить выражение частотной характеристики входного сопротивления в канонической форме для обоих двухполюсников.
Для прямого двухполюсника. Данный
двухполюсник имеет 4 резонанса, причем первый из них – резонанс напряжений.
Найдем ![]() - эквивалентную емкость двухполюсника при
отключенный ветвя с индуктивностью.
- эквивалентную емкость двухполюсника при
отключенный ветвя с индуктивностью.
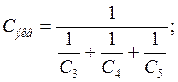
Тогда зависимость будет иметь следующий вид:
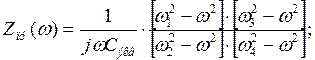
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.