1. Построим схему обратного двухполюсника и рассчитаем параметры его элементов.
Заменим треугольник индуктивностей L2L3L4 эквивалентной звездой и объединим последовательно соединенные L1 и L6; L8 и L5
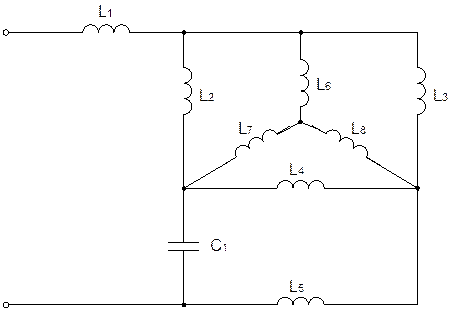
Рассчитаем индуктивности L6,L7,L8,L9 и L10 :
L6=(L2*L3)/(L2+L3+L4)=5.19 мГн
L7=(L2*L4) /(L2+L3+L4)=4 мГн
L8=(L3*L4) /(L2+L3+L4)=2.92 мГн
L9= L1+L6=18.19 мГн
L10= L8+L5=17.92 мГн
После преобразований схема примет вид:
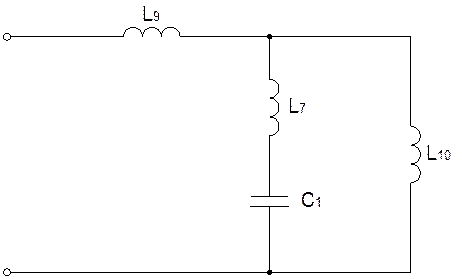
Построим схему обратного двухполюсника:
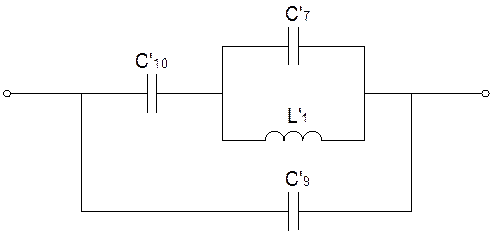
Для определения параметров обратного двухполюсника запишем условия:
![]() где
где ![]() и
и![]() -комплексные
сопротивления исходного и обратного двухполюсников;
-комплексные
сопротивления исходного и обратного двухполюсников;
![]() -коэффициент перехода.
-коэффициент перехода.
1) 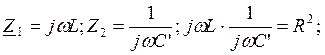 2)
2) 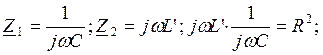
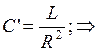
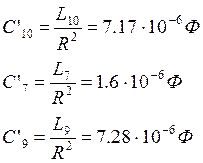
![]()
![]()
2.а) Приведем схему исходного двухполюсника к каноническому виду:
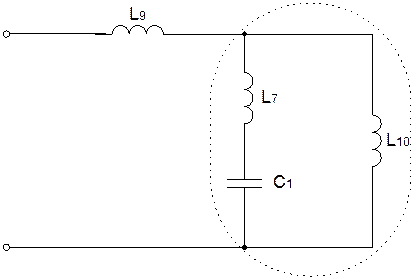
Заменим часть схемы L7С1L10 эквивалентной L11С2L12:
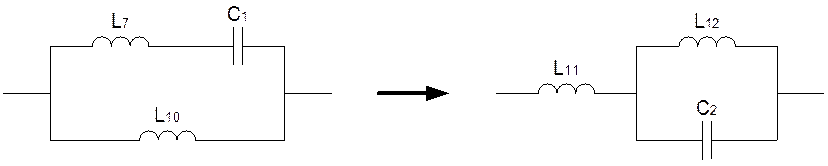

Определим коэффициенты a,b,c,d. Составим выражение входного сопротивления схемы до преобразования:
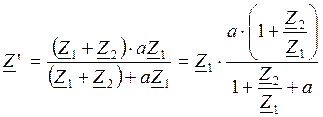
Составим выражение входного сопротивления схемы после преобразования:
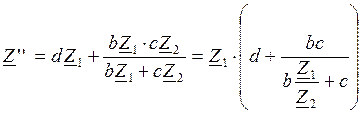
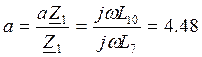
1) ![]()
![]()
![]() 2)
2) ![]()
![]()
![]()
![]()
![]()
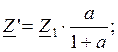
![]()
![]()
![]()
![]()
![]()
![]()
![]()
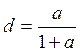
3) ![]()
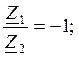
![]()
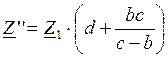
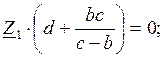
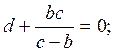
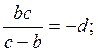
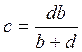
![]()
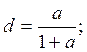
![]()
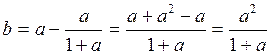
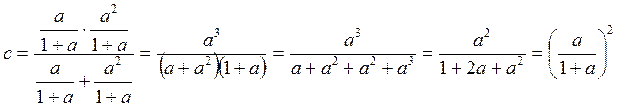
Подставляя числовое значение коэффициента а, получим:
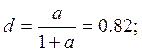
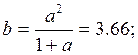
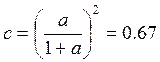
Рассчитаем параметры эквивалентной схемы:
![]()
![]() мГн
мГн
![]()
![]() мГн
мГн
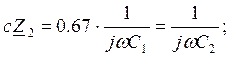
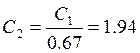 мкФ
мкФ
Получим схему:

![]() мГн
мГн
Исходная схема в каноническом виде:
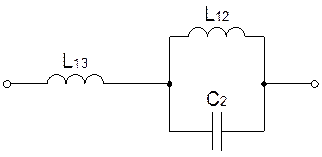
б) Приведем схему обратного двухполюсника к каноническому виду:
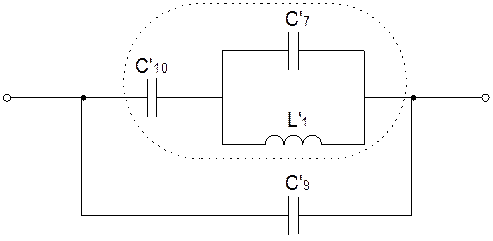
Заменим часть схемы C’7L’1C’10 эквивалентной C’11L’2C’12:
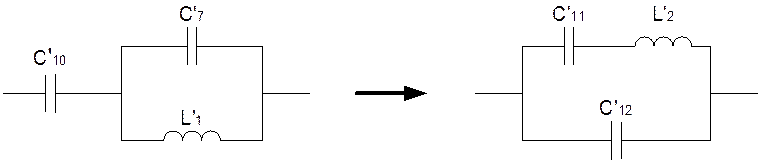

Найдем коэффициенты a,b,c,d:
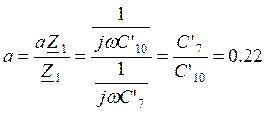
![]()
![]()
![]()
Рассчитаем параметры эквивалентной схемы:
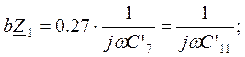
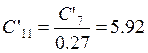 мкФ
мкФ
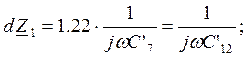
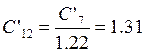 мкФ
мкФ
![]()
![]() мГн
мГн
Получим схему:
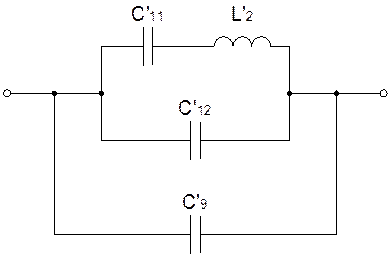
Заменим емкости С’9 и C’12 эквивалентной С’13:
![]() мкФ
мкФ
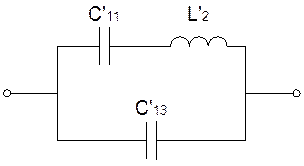
Приведем полученную схему к каноническому виду:
Заменим схему C’11L’2C’13 эквивалентной C’14L’3C’15:
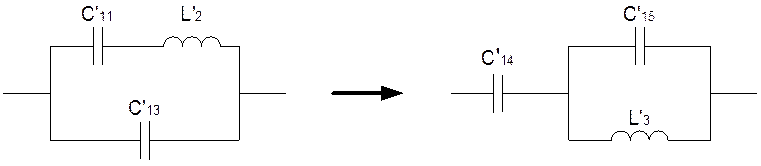

Определим коэффициенты a,b,c,d.
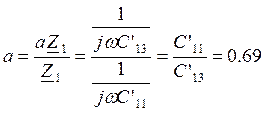
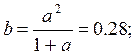
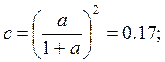
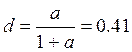
Рассчитаем параметры эквивалентной схемы:
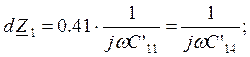
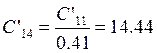 мкФ
мкФ
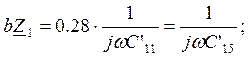
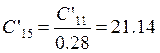 мкФ
мкФ
![]()
![]() мГн
мГн
3.a) Определим все резонансные частоты и характеров резонансов для исходного двухполюсника в канонической форме.
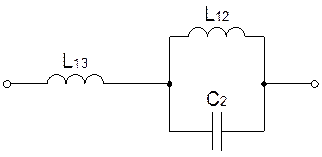
Каноническая
схема содержит три элемента, следовательно, число резонансных частот равно
двум. Так как схема имеет путь для прохождения постоянного тока, то первым
будет резонанс токов с частотой w1,которую
найдем по формуле: 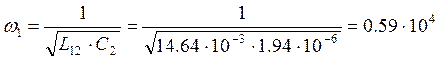
![]()
Частоту резонанса напряжений w2 найдем приравнивая нулю входное сопротивление схемы:
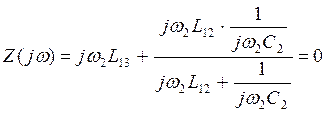
![]()
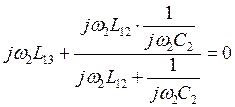
отсюда находим
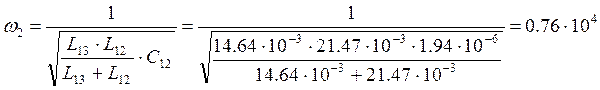
![]()
Построим характеристическую строку:
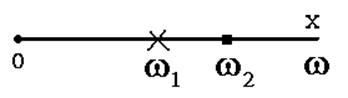
б) Определим все резонансные частоты и характеров резонансов для обратного двухполюсника в канонической форме.
.
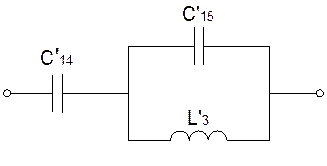
Каноническая схема обратного двухполюсника содержит три элемента, следовательно, число резонансных частот равно двум. Так как схема не имеет пути для прохождения постоянного тока, то первым будет резонанс напряжений с частотой w1, которую найдем, приравнивая ее входное сопротивление к нулю:
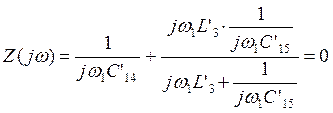
![]()
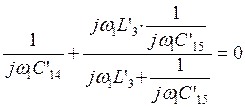
отсюда находим
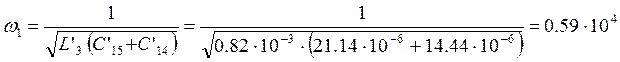
![]()
Далее вычисляем частоту резонанса токов:
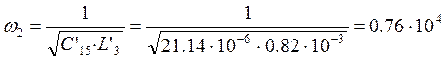
![]()
Построим характеристическую строку:
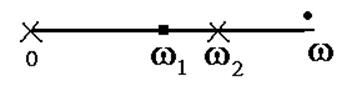
4.а)Запишем зависимость Z(w) для исходного двухполюсника в канонической форме.
Найдем коэффициент Н. Для этого выясним характер сопротивления схемы при w>0. Очевидно, сопротивление схемы имеет индуктивный характер, поэтому Н=L13=21,47 мГн находится из схемы, в которой емкость С2 закорочена. Составим выражение сопротивления схемы Z(jw), при этом учтем, что первым был резонанс токов, поэтому множитель jw должен быть записан в числителе этого выражения:
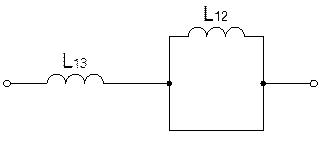
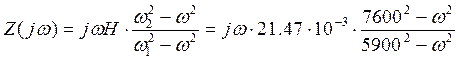
б)Запишем зависимость Z(w) для обратного двухполюсника в канонической форме.
Найдем коэффициент Н. Для этого выясним характер сопротивления схемы при w>0.
Очевидно, сопротивление схемы имеет емкостный характер, поэтому Н=1/Сэ, где Сэ находится из схемы, в которой отключена индуктивность L’3 :
Сэ=С’14С’15/(С’14+С’15)=8.58 мкФ
Отсюда
Н=0,12*106 Ф-1
Составим выражение сопротивления схемы Z(jw), при этом учтем, что первым был резонанс напряжений, поэтому множитель jw должен быть записан в знаменателе этого выражения:
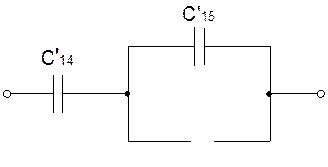
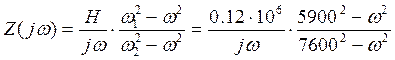
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.