Задача 2.
Расчет корректоров амплитудно-частотных и фазо-частотных характеристик.
1.
Построить требуемые частотные
характеристики АВК и ФВК ![]() и
и ![]() в диапазоне частот
в диапазоне частот ![]() Минимальное затухание АВК на верхней частоте заданного
диапазона должна составлять 5% от рабочего затухания линии на этой частоте.
Минимальное затухание АВК на верхней частоте заданного
диапазона должна составлять 5% от рабочего затухания линии на этой частоте.
2. Выбрать схемы АВК и ФВК и вывести уравнение затухания и фазы контуров.
3. Рассчитать параметры элементов обоих контуров.
4. Произвести проверочный расчет. Расчетные характеристики не должны отличаться от требуемых более чем на 10%.
Исходные данные:
Воздушная двухпроводная линия.
Материал проводов – алюминий.
![]()
Температура окружающей среды – ![]()
Состояние погоды – сухо.
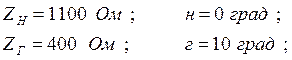
![]()
Действующее значение напряжения на нагрузке при рабочей частоте: ![]()
1.
Произведем расчет первичных
параметров линии и постоянной распространения ![]() .
.
Удельное сопротивление алюминиевого провода
при температуре ![]() .
.
![]()
Находим сопротивление проводов двухпроводной линии при постоянном токе на единицу длины:
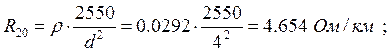
Температурный коэффициент сопротивления для алюминия :
![]()
Находим сопротивление единицы длины линии на
постоянном токе при
температуре t:
![]()
Следующие параметры определим как функции от
частоты, где ![]() .
.
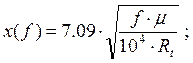
Резистивное сопротивление единицы длины линии при переменном токе находится по формуле:
![]()
где: F(x) – поправочный коэффициент учитывающий увеличение резистивного сопротивления линии вследствие поверхностного эффекта, берется в зависимости от x
Индуктивность двухпроводной воздушной линии на единицу длины при переменном токе находится по формуле:
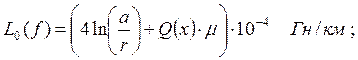
где: Q(x) – коэффициент, учитывающий внутреннюю индуктивность линии.
Находим емкость двухпроводной воздушной линии на единицу длины при переменном токе:
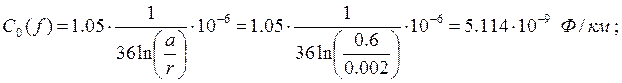
Проводимость изоляции двухпроводной воздушной линии при постоянном токе:
![]()
Коэффициент диэлектрических потерь в изоляторах:
![]()
Проводимость изоляции двухпроводной воздушной линии находим по формуле:
![]()
Находим постоянную распространения линии:
![]()
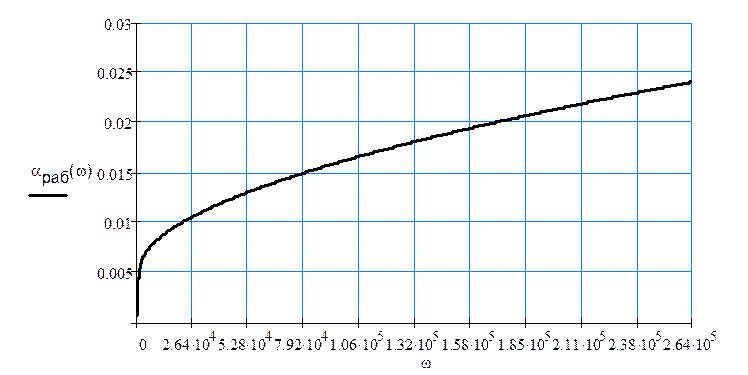
Километрический коэффициент затухания линии равен:
![]()
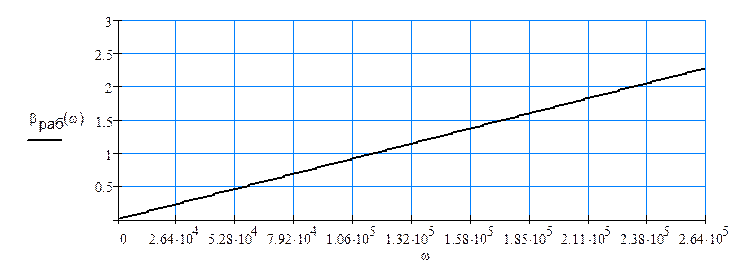
Километрический коэффициент фазы линии равен:
![]()
2.
По рассчитанным ![]() построим:
построим:
![]()
![]()
3. Произведем расчет АВК.
По заданной частотной характеристике затухания корректируемой цепи построим требуемую частотную характеристику затухания.
![]()
![]()
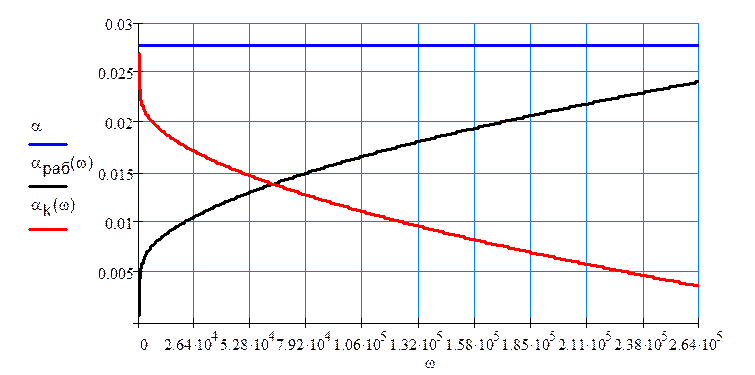
По полученной частотной характеристике АВК выбираем схему АВК 1-го порядка.
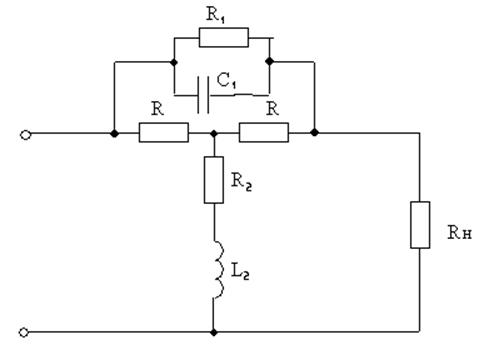
4. Произведем вывод уравнения затухания для выбранной схемы АВК.
Общее уравнение затухания АВК имеет вид:
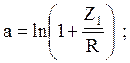
Элемент ![]() представляет собой
параллельное соединения резистора
представляет собой
параллельное соединения резистора ![]() и конденсатора
и конденсатора ![]() . Тогда:
. Тогда:
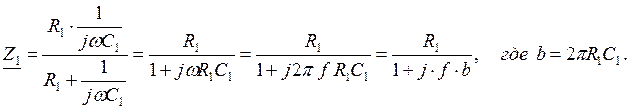
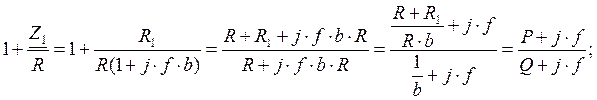
где: 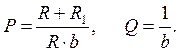
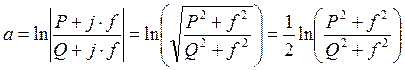
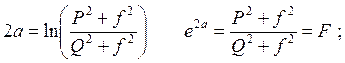
Уравнение затухания АВК первого порядка будет иметь вид:
![]()
5. Определим параметры элементов выбранной схемы АВК.
Составим систему уравнений.
При ![]()
![]()
При ![]()
![]()
Получаем:
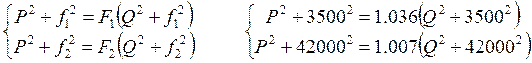
Решая данную систему уравнений, получаем:
![]()
Зная P и Q, найдем параметры элементов контура.
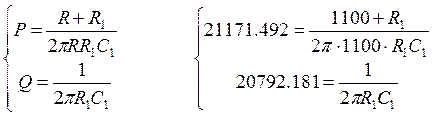
Решая данную систему уравнений, получаем:
![]()
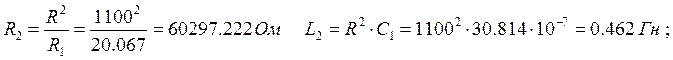
6. Выполним проверочный расчет характеристики затухания контура.
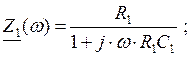
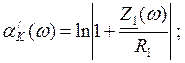
Требуемая и расчетная характеристики АВК имеют вид:
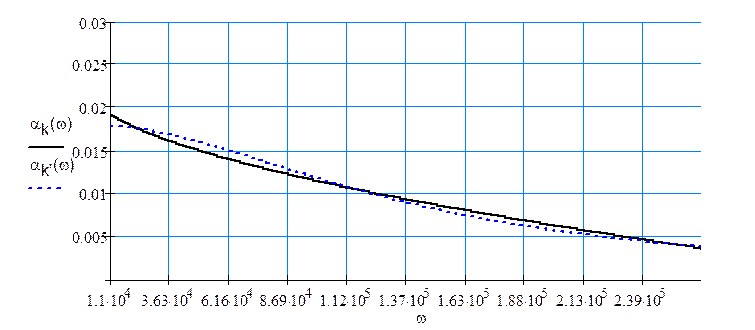
Проверим насколько расчетная характеристика затухания отличается от требуемой.
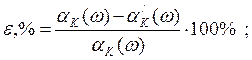
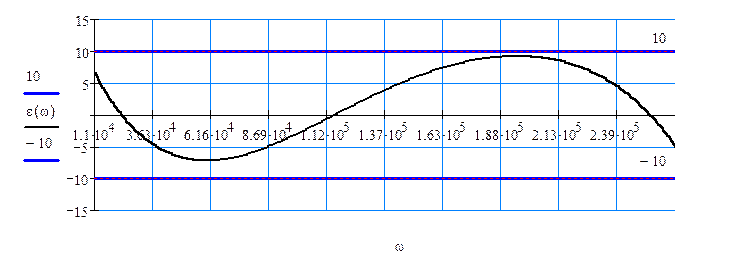
Так как расчетная характеристика затухания отличается от расчетной не более чем на 10%, то выбранная нами схема АВК удовлетворяет всем нашим условиям и выбор более сложной схемы не требуется.
7. Расчет фазовыравнивающего корректора.
Для данной характеристики выполняется условие отсутствия фазочастотных искажений сигналов :
![]()
т.е. характеристический коэффициент фазы прямо пропорционально зависит от частоты, характеристика имеет вид прямой с некоторым угловым коэффициентом k.
Cледовательно для данной частотной характеристики
характеристического коэффициента фазы в заданной цепи в диапазоне частот ![]() построение
фазовыравнивающего корректора не требуется.
построение
фазовыравнивающего корректора не требуется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.