Для обратного двухполюсника. Данный двухполюсник имеет
4 резонанса, причем первый из них – резонанс токов. Найдем ![]() - эквивалентную индуктивность
двухполюсника при закороченных емкостях:
- эквивалентную индуктивность
двухполюсника при закороченных емкостях:
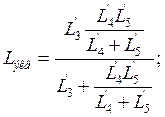
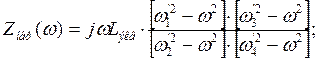
1.5 Рассчитать и построить частотные характеристики входных сопротивлений обоих двухполюсников.
Таблица 1.1 – Расчет частотных характеристик двухполюсников
|
|
Исходный |
Обратный |
|
0 |
|
0 |
|
1000 |
-j501,665 |
j976,748 |
|
2000 |
-j199,514 |
j2456 |
|
2500 |
-j107,048 |
j4577 |
|
|
0 |
|
|
3000 |
j28,543 |
-j17170 |
|
3200 |
j149,105 |
-j3286 |
|
3400 |
j496,04 |
-j987,824 |
|
|
|
0 |
|
4500 |
-j247,945 |
j1976 |
|
6500 |
-j94,652 |
j5177 |
|
7500 |
-j50,733 |
j9658 |
|
|
0 |
|
|
8500 |
j11,881 |
-j41240 |
|
9500 |
j231,201 |
-j2119 |
|
9900 |
j974,501 |
-j502,811 |
|
|
|
0 |
|
15000 |
-j98,454 |
j4977 |
|
25000 |
-j49,202 |
j9959 |
|
35000 |
-j33,955 |
j14430 |
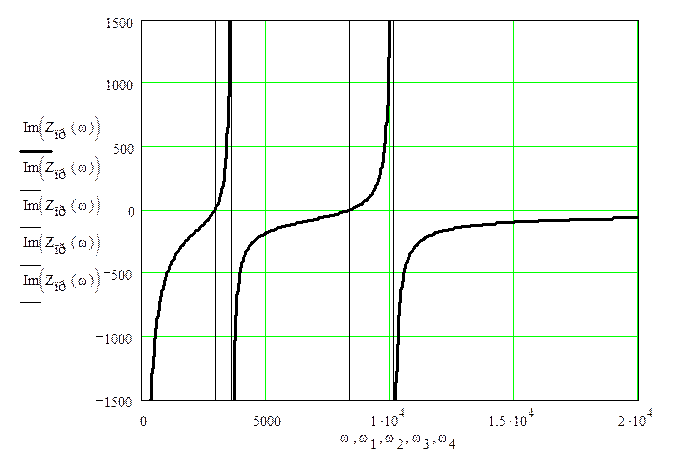
Рисунок 1.7 – Частотная характеристика исходного двухполюсника
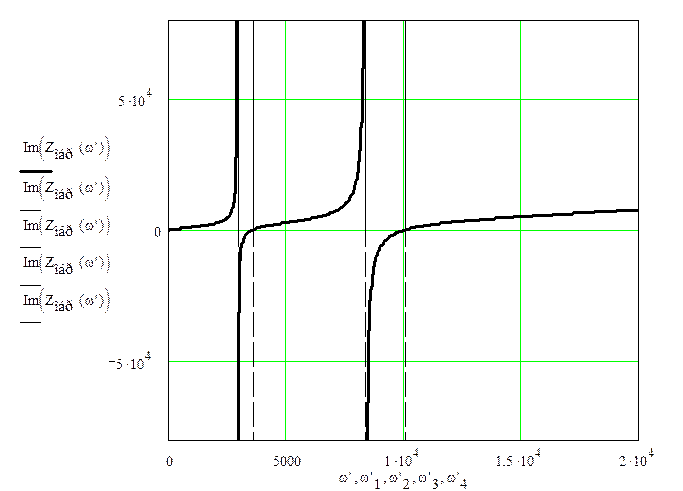
Рисунок 1.8 – Частотная характеристика обратного двухполюсника
Задание на вторую задачу расчетно-графической работы №1:
РАСЧЕТ ЧЕТЫРЕХПОЛЮСНИКОВ
2.1 Представить сложный четырёхполюсник в виде двух простых и определить способ их соединения.
2.2 Определить коэффициенты матриц А элементарных четырёхполюсников, а также коэффициенты других матриц, соответствующих соединению четырёхполюсников.
2.3 Используя правила сложения и умножения матриц, определить коэффициенты матрицы А составного четырёхполюсника.
2.4 Определить собственные и рабочие параметры составного четырёхполюсника.
2.5 Рассчитать и построить зависимости модуля и аргумента входного сопротивления составного четырёхполюсника от сопротивления нагрузки.
2.6 Записать уравнение передачи четырехполюсника в матричной и параметрической формах.
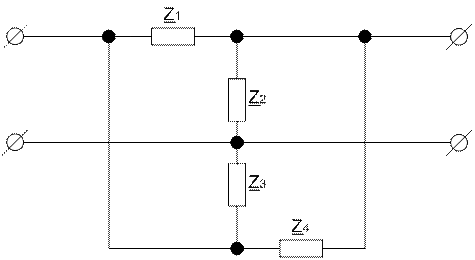
Рисунок 2.1 – Схема четырехполюсника
Исходные данные:
Z1=L=2 мГн; Z2=C=10 мкФ; Z3=R=10 Ом; Z4=L;
Zг=11 кОм; г=+30 град Zн=1,2 кОм; н=+10 град;
f=2 кГц;
2.1 Представить сложный четырёхполюсник в виде двух простых и определить способ их соединения.
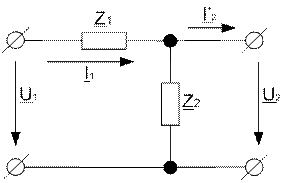
Представим исходный четырехполюсник в виде соединения двух более простых четырехполюсников:
 И
И 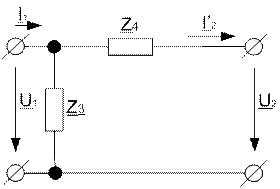
Приведем эквивалентную схему соединения этих двухполюсников:
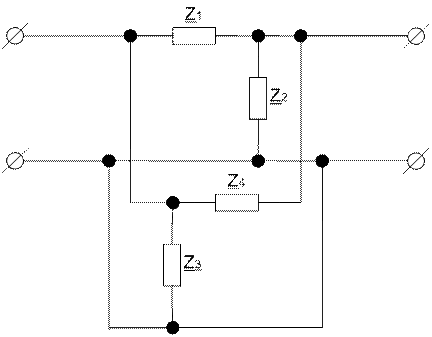
Из рисунка видно, что четырехполюсники соединены параллельно.
2.2 Определить коэффициенты матриц А элементарных четырёхполюсников, а также коэффициенты других матриц, соответствующих соединению четырёхполюсников.
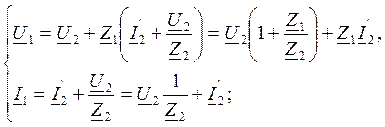
Из этой системы следует, что:
Для первого четырехполюсника имеем:
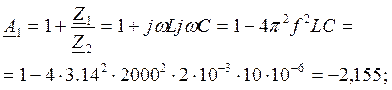
![]()
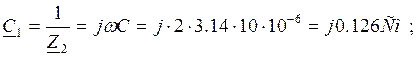
![]()
Для второго четырехполюсника:
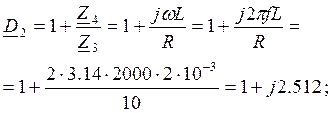
![]()
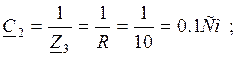
![]()
Найдем коэффициенты матриц ![]() обоих двухполюсников:
обоих двухполюсников:
Для перехода от матрицы ![]() к матрице
к матрице ![]() будем
использовать следующие формулы:
будем
использовать следующие формулы:
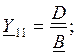
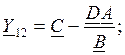
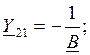
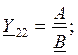
Тогда получим:
Матрица ![]() первого
четырехполюсника:
первого
четырехполюсника:
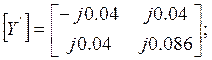
Матрица ![]() второго
четырехполюсника:
второго
четырехполюсника:
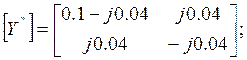
Используя правило сложения матриц
получим матрицу ![]() составного четырехполюсника:
составного четырехполюсника:
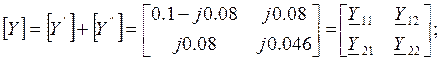
2.3 Используя правила сложения и умножения матриц, определить коэффициенты матрицы А составного четырёхполюсника.
Из матрицы ![]() найдем
матрицу
найдем
матрицу ![]() составного четырехполюсника:
составного четырехполюсника:
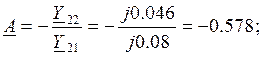
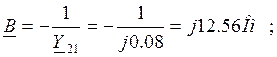
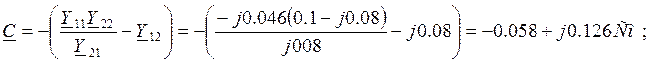
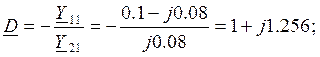
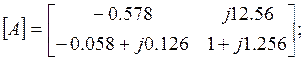
2.4 Определить собственные и рабочие параметры составного четырёхполюсника.
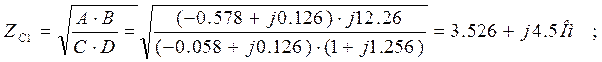
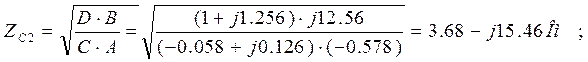
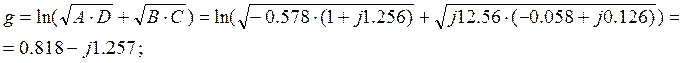
![]()
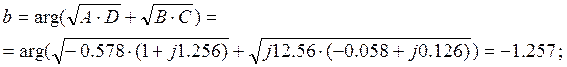
![]()
![]()
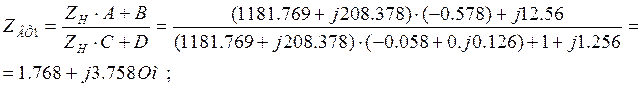
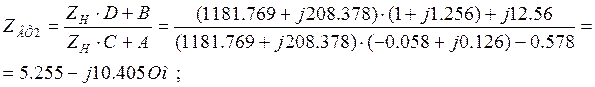
Затухание вызванное несогласованностью на входе.
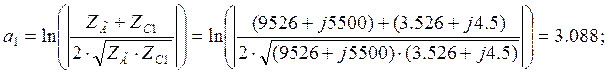
Затухание вызванное несогласованностью на выходе.
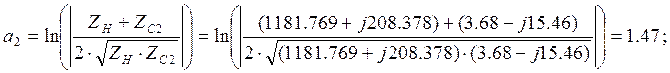
Коэффициент отражения на входе
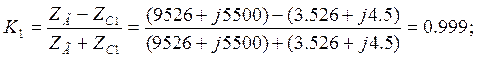
Коэффициент отражения на выходе
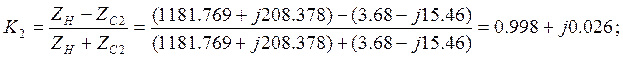
Затухание вызванное взаимодействием отражений
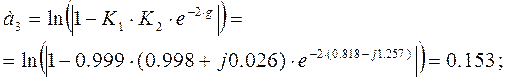
Рабочее затухание
![]()
Затухание вызванное несогласованностью ![]() и
и ![]()
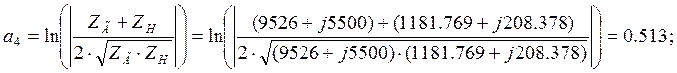
Вносимое затухание
![]()
2.5 Рассчитаем и построим зависимости модуля и аргумента входного сопротивления составного четырёхполюсника от сопротивления нагрузки.
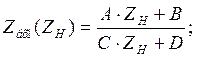
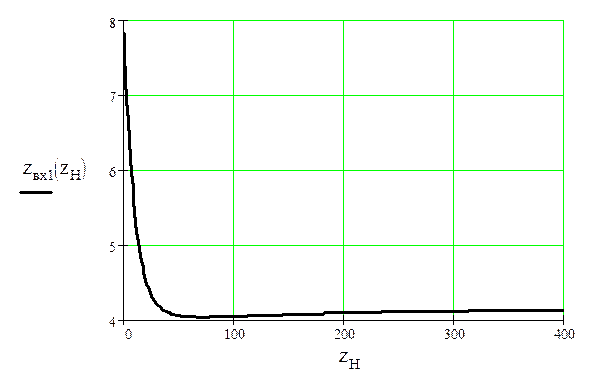
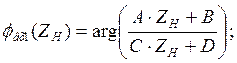
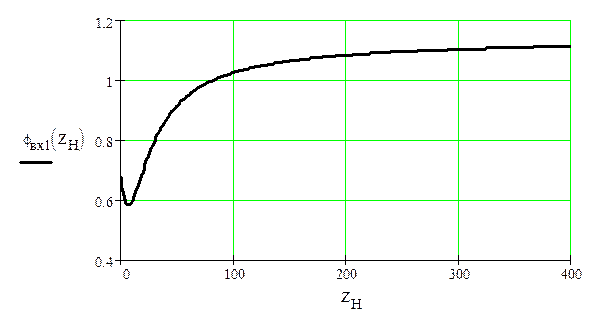
2.6 Запишем уравнение передачи четырёхполюсника в матричной и параметрической формах
Уравнение передачи четырёхполюсника в матричной форме
![]()
![]()
Уравнение передачи четырёхполюсника в параметрической форме
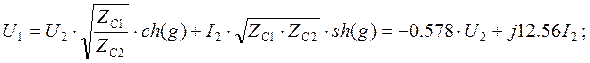
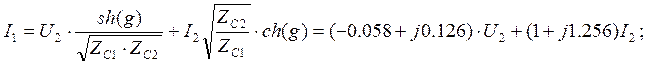
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.