Завод отправил на базу 500 доброкачественных изделий. Для
каждого из изделий вероятность повреждения в пути равна 0.002. Найти
вероятность того, что среди прибывших на базу изделий будет нее более трех
поврежденных (0.981).
Решение:
Поскольку случайная величина X
характеризует число появлений события А в серии из n независимых испытаний, в каждом из которых это событие может
осуществляться с вероятностью p, то она распределена
по биномиальному закону. Возможные значения данной случайной величины: 0,1,2,…,n, а вероятность каждого из значений определяется по формуле:
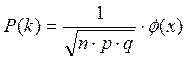
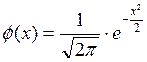
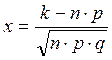
где q=1-p
Теперь можно вычислить вероятность события A={в
пути повредится не более 3 изделий}:
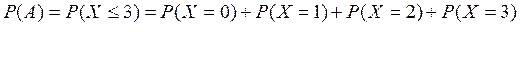
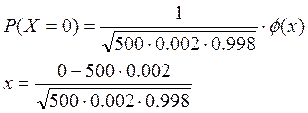
P(X=0)=0.242
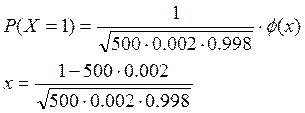
P(X=1)=0.399
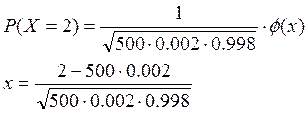
P(X=2)=0.242
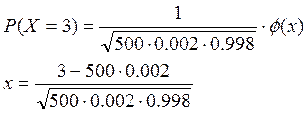
P(X=3)=0.054
P(A)=0.0937
Ответ: вероятность того, что в пути не произойдет
повреждения более 3 изделий, равна 0.937.
