Случайные величины: Расчетно-графическая работа № 2

Министерство Образования Республики Беларусь

Белорусский государственный университет транспорта

Электротехнический факультет

Кафедра прикладной математики

Расчетно-графическая работа №2

Случайные величины

Вариант 47

Выполнил                               Проверил

студент гр. ЭС-21               доцент

Рубцов К.М.                          Шевченко Д.Н.

2005

Задание №1

          Вероятность поступления вызова на АТС в течение 1 мин. равна 0.4. Случайная величина Х – число вызовов, Поступивших на АТС в течение 4 минут. (M[X]=1,6; D[X]=0,96)

          Для определенной в условии задачи дискретной случайной величины :

1. Построить ряд распределения и столбцовую диаграмму.

2. Найти функцию распределения и построить ее график.

3. Вычислить числовые характеристики : математическое ожидание, моду,

    дисперсию, среднее квадратическое отклонение.

Решение

1. Рассмотрим события :

A_i = {в течение 4 минут поступило i-е количество вызовов}, i=0,1,2,3,4      

Вероятности событий A_i, можно найти по формуле Бернулли (p = 0.4, q = 0.6) :

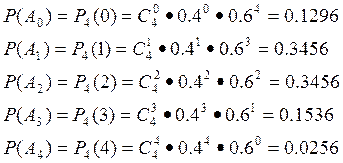
Следовательно, ряд распределения случайной величины можем записать в виде

Xi	0	1	2	3	4
Pi	0.1296	0.3456	0.3456	0.1536	0.0256

Построим столбцовую диаграмму :

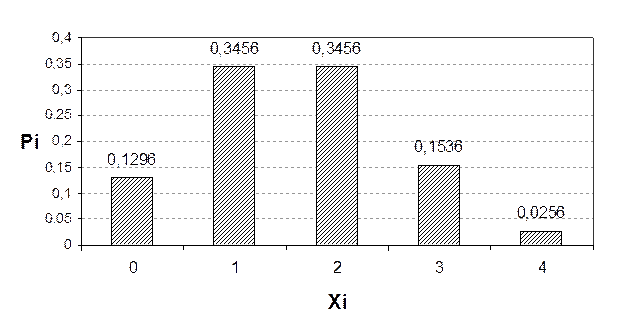
2.

Функция распределения дискретной случайной величины – ступенчатая функция, имеющая разрывы в точках x_i, , где  n – число значений случайной величины, а в промежутках (-∞, x_i], (x_i, x_i+1], , (x_п,∞), принимающая постоянное значение. Вычислим функцию F(x) распределения исследуемой случайной величины :

                    F(x) = P{ξ<x}

          F(0) = P{ξ<0} = 0

          F(1) = P{ξ<1} = 0.1296

          F(2) = P{ξ<2} = 0.4752

          F(3) = P{ξ<3} = 0.8208

          F(4) = P{ξ<4} = 0.9744

          F(5) = P{ξ<5} = 1

                   0;          x£0

                   0.1296;  0<x£1

F(x) =         0.4752;  1<x£2

                   0.8208;  2<x£3

                   0.9744;  3<x£4

                   1;           4<x£∞

Изобразим график функции F(x) :

 

3. Вычислим числовые характеристики случайной величины ξ :

а) математическое ожидание случайной величины ξ :

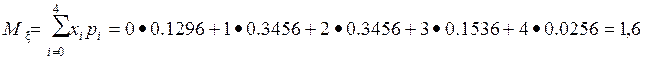
б) мода случайной величины ξ равна ее наиболее вероятному значению :

mod ξ = 1

mod ξ = 2

в) дисперсия случайной величины ξ :

 

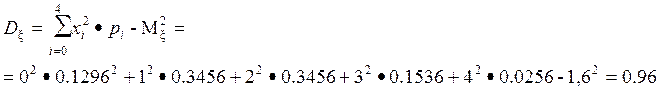
г) среднее квадратическое отклонение случайной величины ξ :

Выводы : среднее значение поступивших в течение 4 минут вызовов  - 1.6; наиболее вероятное количество поступивших в течение 4 минут вызовов - 1;2, среднее квадратическое отклонение от среднего значения равно 0,98.

Задание №2

Закон распределения непрерывной случайной величины задан функцией плотности распределения вероятностей f(x). Требуется :

          1. Определить значение параметра С.

          2. Построить график функции плотности распределения вероятностей.

3. Найти функцию распределения случайной величины и построить ее   график.

4. Вычислить числовые характеристики данной случайной величины: математическое ожидание, моду, медиану, дисперсию, среднее квадратическое отклонение.

5. Найти вероятность того, что данная случайная величина примет значение, принадлежащее отрезку [a;b].

                        C(1-x²), xÎ[-1;1];

f(x)=      

                        0,     xÏ[-1;1];

a = - 0.5; b = 0.5;

Решение

1. Для определения неизвестного параметра С воспользуемся соотношением

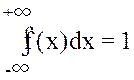
 В данном случае имеем

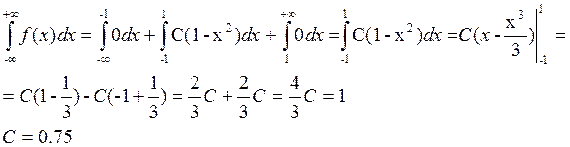
 Таким образом, функция плотности распределения имеет вид :

           0.75(1-x²), xÎ[-1;1];

        f(x)=      

                 0,         xÏ[-1;1];

 

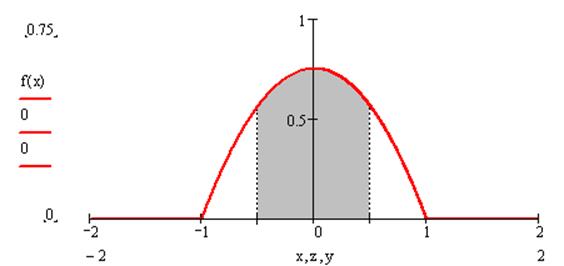
  2. Построим график функции f(x) :

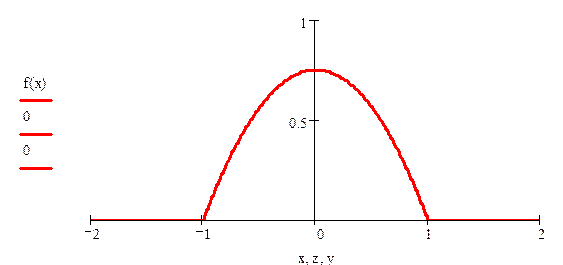
  3. Вычислим функцию распределения данной случайной величины

 

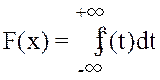
При xÎ(-∞, -1]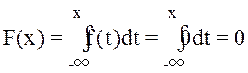 

При xÎ(-1, +1)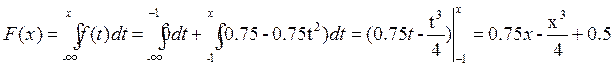   

При xÎ[1, +∞)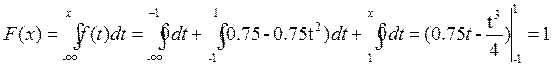 

 

                        0                           при  xÎ(-∞,-1)  

Итак, F(x)=     0.75x – x³/4+0.5  при  xÎ[-1,1]

                       1                            при  xÎ(1,∞)

График функции F(x) :

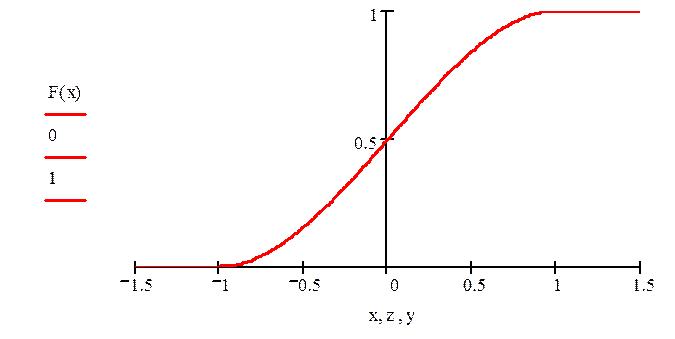
4. Вычислим случайные характеристики данной случайной величины :

Математическое ожидание :

M[X] = 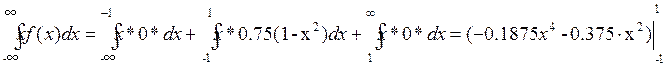= 0

Для вычисления дисперсии воспользуемся формулой :

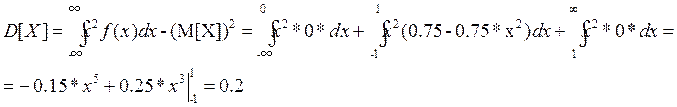
Среднее квадратическое отклонение :

Мода данной случайной величины, как следует из графика фукнции f(x), равна нулю, аналогично медиана также равна 0.

5. Для вычисления вероятности того, что случайная величина Х примет значение, принадлежащее промежутку  [-0.5;0.5], можно воспользоваться соотношением:

P(a≤X≤b) = F(b)-F(a)=0.844-0.156=0.688

В данном случае :

На рисунке выделена фигура, площадь которой равна вероятности

P(-0.5≤X≤0.5) = 0.6875

Выводы: Значение параметра С=0,75, М[X]=0, D[X]=0.2, , вероятность того, что данная случайная величина примет значение, принадлежащее отрезку [-0.5;0.5] равна 0,6875.

Задание №3

Найти среднее число опечаток на странице рукописи, если верояность того, что страница рукописи содержит хотя бы одну опечатку, равна 0,95. (Предполагается, что число опечаток распределено по закону Пуассона.) (3)

Решение.

По условию задачи число опечаток распределено по закону Пуассона