Определение вероятности наступления события методами максимального правдоподобия, наименьших квадратов и наименьших сумм

Общие положения

Пусть из n испытаний событие A наступило m раз. Требуется определить вероятность наступления события A.

Учитывая смысл данного опыта и аксиомы Колмогорова, приходим к выводу о том, что вероятность наступления события A P(A) = p(^) будет принадлежать промежутку от нуля до единицы: 0 P(A) 1.

Метод максимального правдоподобия.

Идея метода максимального правдоподобия состоит в том, что вероятность события A предполагается таковой, что из n испытаний событие A скорее всего наступит фактически наблюдавшееся число раз (т.е. m), т.о. вероятность наступления события P_n(m|P(A)=p)®max.

Вероятность того, что событие A наступит m раз из n испытаний P_n(m) определяется по формуле Бернулли:

.

В точке максимума производная функции 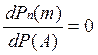 (а функция )

Вероятность наступления события А будем обозначать P(A)= p.

Тогда

- постоянная и, следовательно, может быть сокращена. Поэтому

Заметим, что значение функции  не может быть

Получаем, что 

Что равносильно  или  .

Т.е. . Так выглядит оценка вероятности наступления события А методом максимального правдоподобия, если это событие наступило m раз из n испытаний.

Метод наименьших квадратов.

g(A)-вероятность наступления события A в i-м испытании. Если событие A наступило в i-м испытании, то оно является достоверным и g_i(A)=1, а если собыите A не наступило в i-м испытании, то оно является невозможным, его вероятность g_i(A)=0.

Введем величину .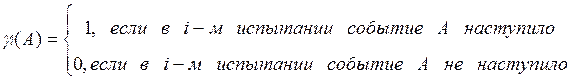

Cуть метода наименьших квадратов в том, что сумма квадратов разностей g_i(A) и P(A) для всех испытыний является наименьшей, т.е..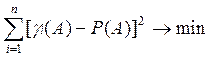

Используем свойство квадрата разности: .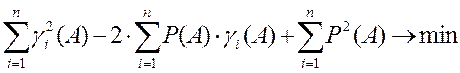

Учитывая, что P(A)- величина постоянная и то, что g2 i (A)= g_i(A) (1²=1,0²=0) , получаем :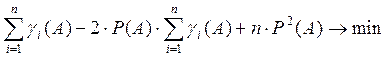

По смыслу введенной величины g_i(A) 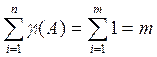, тогда .

В точке минимума производная данной функции по dP(A) равна нулю.

Отсюда 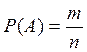. Так выглядит оценка вероятности наступления события А методом наименьших квадратов, если это событие наступило m раз из n испытаний. Заметим, что она совпадает с оценкой вероятности наступления события А методом максимального правдоподобия.

Метод наименьших сумм

g(A)-вероятность наступления события A в i-м испытании. Если событие A наступило в i-м испытании, то оно является достоверным и g_i(A)=1, а если собыите A не наступило в i-м испытании, то оно является невозможным, его вероятность g_i(A)=0.

Введем величину .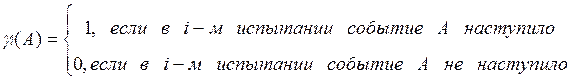

Смысл метода наименьших сумм в том, что сумма разностей g_i(A) и P(A) для всех испытыний является наименьшей, т.е..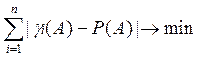

Заметим, что величина g_i(A)=1 наблюдается mраз, eсли событие Aпроизошло m раз из n а g_i(A)=0 наблюдается во всех остальных случаях, т.е m−n раз.

Поэтому .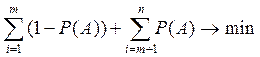

Или ,

что равносильно  (здесь p=P(A)).

Введем величину q=(1-p) − вероятность того, что событие A не произошло в конкретном испытании и величину  − количество испытаний, в которых событие A не произошло: .

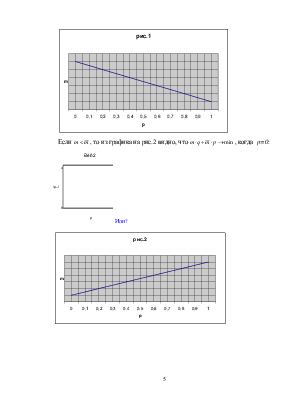
Проанализируем данное выражение графически:

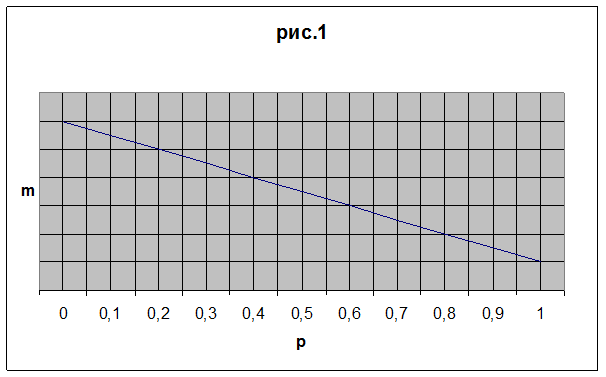
Если , то из графика на рис.1 видно, что , когда p=1:

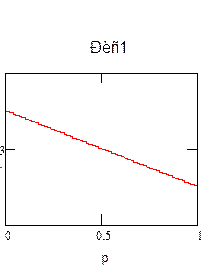Какой рисунок лучше оставить ?

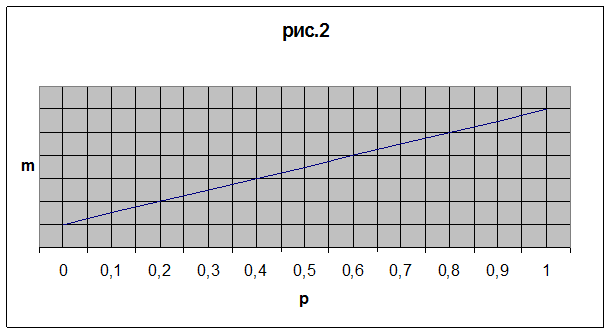
Если , то из графика на рис.2 видно, что , когда p=0:

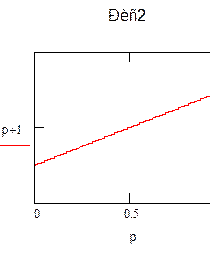 Или?