Описание метода половинного деления
Решается уравнение вида ex - e-x -2 = 0 (1)
с заданной точностью ![]()
Значение х, при котором
функция f(![]() тождественно равна нулю -
тождественно равна нулю - ![]() )=0 называется корнем уравнения (1).
А способ нахождения этого значения
)=0 называется корнем уравнения (1).
А способ нахождения этого значения
х - решением уравнения
Корни данного уравнения предлагается найти методом деления отрезка пополам.
Для этого используем:
1. Графический способ решения уравнения.
2. Метод приближенных вычислений: деления отрезка пополам
При этом приходится решать две задачи:
1. отделение корней, т.е. отыскание малых областей (границ отрезка
[a ,b], в каждом из которых заключен один и только один корень уравнения)
2. вычисление корней с заданной точностью.
При выделении областей (границ отрезка [a ,b]), в которых находятся
действительные корни уравнения (1) , можно воспользоваться следующим свойством: если на концах некоторого отрезка непрерывная функция f(x) принимает значения противоположных знаков, то на этом отрезке уравнение f(x)=0 имеет один корень.
Определить отрезок [a , b], содержащий один корень, можно графическим способом.
Решить уравнение графически - это значит найти точку пересечения графика функций f(x) с осью 0Х.
Решить уравнение с точностью ![]() - значит найти отрезок длиной <
- значит найти отрезок длиной <![]() на оси 0х, в котором находится
корень уравнения. Длина отрезка - есть степень точности .
на оси 0х, в котором находится
корень уравнения. Длина отрезка - есть степень точности .
Считается, что корень уравнения отделен на отрезке оси 0х, если этот корень содержится на данном отрезке и на этом отрезке других корней нет.
Решить уравнение с
точностью ![]() , значит найти разность конечных значений
данного отрезка. Эта разность должна быть
, значит найти разность конечных значений
данного отрезка. Эта разность должна быть ![]() (т.е. в - а
(т.е. в - а ![]() ).
).
Для того чтобы решить уравнение с заданной точностью применяются методы приближенных вычислений. Мы воспользуемся методом половинного деления.
При выделении областей, в которых находятся действительные корни
уравнения (1) можно воспользоваться следующим свойством:
если на концах некоторого отрезка непрерывная функция f(x) принимает значения противоположных знаков, то на этом отрезке уравнение f(x)=0 имеет один корень (т.е. f(a)*f(b) < 0). Или Если функция непрерывна и монотонна на отрезке [a , b] и принимает на концах отрезка значения разных знаков, то корень находится внутри этого отрезка.
Уточнение корня до
точности ![]()
Если b - a >![]() , то необходимо сужать интервал, на котором
отделен корень для этого применяем метод проб, в частности разновидность этого
метода - метод половинного деления (метод деления отрезка пополам).
, то необходимо сужать интервал, на котором
отделен корень для этого применяем метод проб, в частности разновидность этого
метода - метод половинного деления (метод деления отрезка пополам).
Для нахождения корня
уравнения f(x) = 0 делят отрезок пополам, т.е. выбирают начальное
приближение равным ![]()
![]() .
.
Если (x![]() )=0, то х
)=0, то х![]() является
корнем уравнения. В противном случае выбирают тот из отрезков [ a , x
является
корнем уравнения. В противном случае выбирают тот из отрезков [ a , x![]() ] или [x
] или [x![]() ,b], на концах которого функция f(x) имеет разные
знаки, ибо корень лежит на этой половине. Для случая, изображенного на рис.1. ,
выбирают интервал [x
,b], на концах которого функция f(x) имеет разные
знаки, ибо корень лежит на этой половине. Для случая, изображенного на рис.1. ,
выбирают интервал [x![]() ,b]. Данный
интервал вновь делят пополам и выбирают ту половину, на концах которой функция
имеет противоположные знаки , и т.д.
,b]. Данный
интервал вновь делят пополам и выбирают ту половину, на концах которой функция
имеет противоположные знаки , и т.д.
В результате на каком-то
этапе получим либо точный корень уравнения f(x)=0, либо такой
отрезок, внутри которого находится корень уравнения и длина которого меньше ![]() .
.
![]()
Алгоритм уточнения корней методом половинного деления.
 |

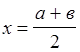 -
вычисление абсциссы середины отрезка (а,в)
-
вычисление абсциссы середины отрезка (а,в)

y = f(x) - вычисление значений функции на концах отрезка
z = f(a)
 |
|||||||
 |
|||||||
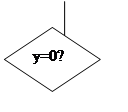
 да
да
![]() y, x
y, x
![]()
![]() нет
нет
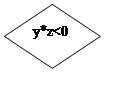 |
да нет
![]()
![]()
![]()
![]()
![]() y * z < 0
y * z < 0
|
|
b - уменьшаем длину отрезка
![]()
![]() ( а,в) путем переноса
точки
( а,в) путем переноса
точки
"а" в точку "х".


![]() нет
нет
да
 |
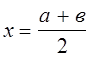
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.