Подобным образом можно определить и методическую погрешность, возникающую при подключении в токовую цепь амперметра, имеющего собственное сопротивление RA.
Вывод: в данном случае присутствуют методическая и инструментальная (класс точности) погрешности.
Метод расчета методической погрешности: математическое моделирование измерительной процедуры.
Приложение П 2.3. Суммирование составляющих погрешности измерения.
Представление результата измерения
Согласно теории вероятностей среднеквадратическое значение отклонения суммы двух величин от ее математического ожидания [3. с.70]:
(2.32)
где s1 и s2 – среднеквадратические отклонения слагаемых от их математических ожиданий, r – коэффициент корреляции.
Зависимыми сильно коррелированными погрешностями обычно оказываются погрешности, обусловленные одной общей причиной. Например, изменение напряжения общего источника питания и вызванное этим убывание чувствительности приборов.
На практике для сильно коррелированных погрешностей принимают r= +1 или –1. В этом случае согласно (2.32) sS = s1 + s2.
Если в рассматриваемом примере отдельные приборы питаются от независимых источников питания, то погрешности не коррелированны и r = 0, следовательно:
.
Это правило теории вероятностей в равной степени относится как к случайным, так и к систематическим погрешностям. Особенность формулы (2.32) в том, что она справедлива независимо от законов распределения погрешностей.
При подсчете суммарной погрешности сначала складываются алгебраически сильно коррелированные погрешности, а затем полученный результат и слабо коррелированные погрешности – средне геометрически.
По нормируемым метрологическим характеристикам средств
измерения можно определить только предельные значения составляющих 
i погрешности
измерения . Если значения всех i симметричны, т.е. i =
А,
то модуль предельного значения погрешности измерения при сильной корреляции
находится путем арифметического суммирования модулей составляющих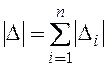 
.
После этого результат измерения можно представить в виде
Х .
Правила записи и округления результатов измерения Х и :
1.
В выражении погрешности удерживается не
более двух значащих цифр, причем последняя цифра обычно округляется до нуля или
пяти. Две цифры следует обязательно удерживать, если цифра старшего разряда
менее трех:
U = 756,45 ±23,47 – не правильно.
2.
Число, выражающее результат измерения Х, должно оканчиваться цифрой того
же разряда, что и предельное значение погрешности измерения . Если первая (слева) из отбрасываемых
цифр больше или равна пяти, то последняя сохраняемая цифра увеличивается на
единицу. При этом лишние цифры в целых числах замещаются нулями, а в десятичных
дробях отбрасываются:
U = 756,45 ±25 – не правильно, U = 756 ±25 – правильно.
При промежуточных вычислениях используется на один разряд больше, чем в конечном результате:
U = 756,4 ±25 – правильно.
3. Округление результатов расчетов осуществляется после их завершения для исключения накапливания ошибок на промежуточных этапах:
U = 756 ±25 – правильно.
При записи результата измерения без указания погрешности в числе оставляются только те цифры, за достоверность которых можно ручаться. Например, записи U = 2,4×103 В и 2400 В не тождественны. Первая запись означает, что верны цифры тысяч и сотен вольт и истинное значение может быть, например, 2,42 или 1,38 В. Запись 2400 В означает, что верны и единицы вольт, истинное значение может быть 2400,2 или 2399,8 В, но не 2420 или 2380 В.
Пример: В результате измерения получено напряжение 3720 В с погрешностью 1%. Результат (без записи погрешности) измерения: 37×102 В, или 3,7×103 В, или 3,7 кВ.
Вопросы
1. Какая погрешность: основная или дополнительная обозначается на лицевой панели измерительных приборов (класс точности)?
2. Почему для обозначения класса точности у разных измерительных приборов используются приведенная, относительная или абсолютная погрешности?
3. Приведите примеры корреляции погрешностей измерительных приборов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.