Теория погрешностей. Основные виды погрешностей, их классификация, страница 5

Если на приборе класс точности указан в виде числа, заключенного в окружность, то он равен пределу допускаемой основной относительной погрешности . При этом абсолютная погрешность прибора определится из выражения

                                                      =Х_ИЗМ / 100%.                                                       (2.3)

 Если на приборе класс точности указан  в виде числа, например, 1.5, то он численно равен пределу допускаемой основной приведенной погрешности . При этом абсолютная погрешность прибора определится из выражения

              =  Y_НЗ / 100%.          (2.4)

Аналогично, классом точности нормируется  при его обозначении на приборе в виде двух чисел, записанных через дробь, например, 0.02/0.01. Но при этом само значение определяется из соотношения (ГОСТ 8401-70)

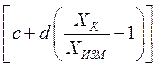                                                     = ,                                           (2.5)

где c и d - числа, задаваемые классом точности (приведенные погрешности в конце и начале шкалы соответственно), причем всегда c/d >1.

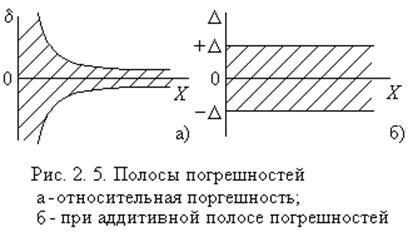
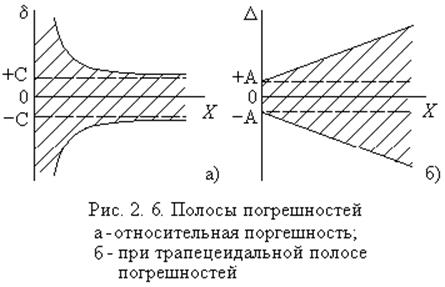Из рис. 2.5, 2.6 следует, что при задании класса точности согласно (2.2, 2.5) относительная погрешность растет обратно пропорционально уменьшению измеряемой величины.  Необходимо проводить измерения в последних 70% шкалы прибора.

У аналоговых приборов это обычно осуществляется с помощью переключения предела измерения с кратностью «100–30–10–3–1» для получения одинаковых погрешностей диапазонов.

У цифровых приборов диапазоны кратны 10 (для удобства восприятия). Однако, выражение (2.1) для этих приборов не применимо. Например, у цифрового вольтметра с выбранным диапазоном 100 В при измерении 11 В относительная погрешность в 10 раз больше, чем при измерении 100 В. Поэтому для задания класса точности цифровых приборов используется выражение (2.5).       

Это позволяет замедлить рост относительной погрешности к началу диапазона.

Если класс точности задан выражением (2.1), то не рекомендуется проводить измерения в начале шкалы прибора, т. к. здесь это уравнение сделать достоверным физически невозможно.

Результат измерения с учетом погрешности может быть записан в виде:

Y = Х_ИЗМ  .

Измерение параметров электрических цепей

 косвенными методами

Определение инструментальной погрешности при косвенных измерениях

При косвенных измерениях значение искомой величины Yнаходят на основании зависимости, связывающей эту величину с одной или несколькими величинами ( x, y, ..., w ), измеряемыми прямыми методами [9, с. 45]:

Y = f ( x, y, ..., w ).                                                   (2.6)

Погрешность результата Yтакже будет связана функционально с погрешностями измеряемых величин x, y, ..., w.

Значения x, y, ..., w обычно находят путем прямых измерений и их погрешности определяются чаще всего пределами допускаемых погрешностей применяемых СИ. В зависимости от применяемых методов и СИ, а также от условий, в которых производятся измерения величин x, y, ..., w, значения их погрешностей независимы или коррелированны между собой. При этом коэффициент корреляции, как правило, остается неизвестным. В таких случаях приходится ориентироваться на наихудший случай, полагая коэффициент корреляции равным 1.

Для нахождения погрешности результата косвенного измерения  можно воспользоваться следующими правилами [П 2.3]:

1. Если окончательный результат измерения выражается суммой или разностью двух или более измеренных значений

Y = x + ... + z - ( u + ... + w ),                                        (2.7)

и погрешности _x , ..., _w независимы и случайны, то абсолютная погрешность результата может быть найдена по формуле

                       _Y =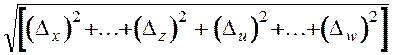.                       (2.8)

Когда погрешности аргументов коррелированны, значение _Y может превышать полученное по формуле (2.8), но всегда удовлетворяет условию

                                      _{Y x} + ... + _z + _u + ... + _w               (2.9)

2. Если окончательный результат измерения выражается произведением или частным двух или более измеренных значений:

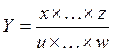                                                          ,                                                    (2.10)