Рабочие условия характеризуются рабочей областью значений влияющих величин, при которых СИ работоспособно и соответствует утвержденным характеристикам.
Нормальные и рабочие значения указываются в паспортных данных и устанавливаются в стандартах, номера которых обычно обозначаются непосредственно на СИ.
Дополнительная – погрешность из-за отклонения одной из влияющих величин от нормального значения.
Эта погрешность нормируется коэффициентами влияния, например, в процентах от основной погрешности при изменении температуры на каждые 100 С. Как правило коэффициенты считают линейными, хотя на самом деле это не так.
Погрешность отсчитывания: в приборах с цифровым отсчетным устройством не превышает одного кванта шкалы отсчетного устройства и включается в состав основной погрешности прибора, в приборах с аналоговым отсчетным устройством в основной погрешности не учитывается. Ее предельное значение для аналоговых приборов определяется формулой
![]() ,
,
где К – коэффициент, значение которого зависит от того, до каких долей деления производится округление при отсчете (если до половины, то К = 0,5); ЦД - цена деления.
Полоса погрешностей
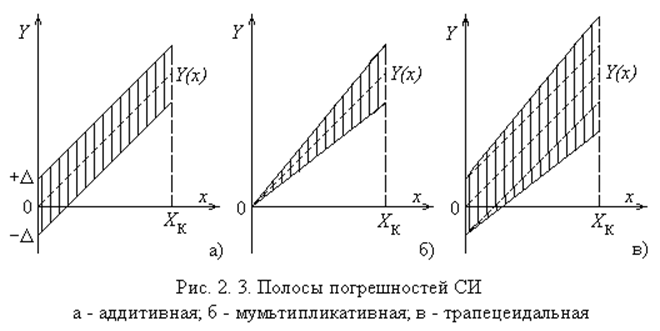 |
Если для СИ характерно постоянное значение абсолютной погрешности (порог чувствительности, смещение «0» начала отсчета и т.д.), то она называется аддитивной (рис. 2.3, а).
Когда ширина полосы возрастает пропорционально росту входной величине X, то погрешность называется мультипликативной (коэффициента передачи усилителя, функции преобразователя) или погрешностью чувствительности (рис. 2.3, б).
Однако реально приборов с чисто мультипликативной погрешностью нет, так как невозможно создать прибор с нулевым значением погрешности при X = 0.
Если погрешность включает обе составляющие, то она изображается полосой трапецеидальной формы (рис. 2.3, в).
Понятие полосы погрешностей одинаково применимо как к случайным, так и систематическим погрешностям.
(ГОСТ 8.401 – 80)
Для нормирования погрешностей СИ используется класс точности, который в числовой форме обозначается на шкале прибора и указывается в паспортных данных.
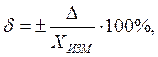 (2.1)
(2.1) 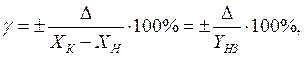 (2.2)
(2.2)
где индексы «к» и «н» соответствуют концу и началу диапазона измерений, YНЗ – нормирующее значение.В качестве YНЗпринимается:
– верхний предел измерения, если нулевая отметка находится на краю или вне шкалы;
– сумма модулей нижнего и верхнего пределов измерения, если ноль внутри шкалы;
– номинальное значение измеряемой величины.
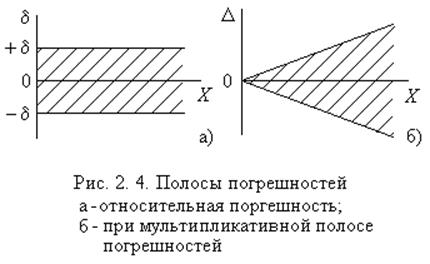
Уравнения (2.1, 2.2, 2.5) служат для расчета погрешностей:
– относительной:
а) мультипликативной (2.1);
б) трапецеидальной (2.5);
– приведенной (2.2).
Используя
уравнения (2.1, 2.2, 2.5), построены
графики ![]() и
и ![]() в зависимости
от величины X (рис. 2.4, 2.5, 2.6).
в зависимости
от величины X (рис. 2.4, 2.5, 2.6).
Эти
графики позволяют оценить соотношение между ![]() и XИЗМ для различных участков
шкалы прибора X.
и XИЗМ для различных участков
шкалы прибора X.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.