Теория погрешностей. Основные виды погрешностей, их классификация, страница 6

и погрешности _x , ..., _w независимы и случайны, то относительная погрешность результата может быть найдена по формуле

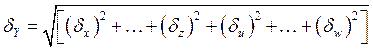                             .                            (2.11)

При косвенных измерениях большим количеством приборов используется, как правило, средне геометрическое сложение погрешностей, т. к. погрешности отдельных приборов имеют разброс значений случайного характера и с учетом знака могут частично компенсировать друг друга.

Когда погрешности аргументов коррелированны, значения _Y могут превышать полученное по формуле (2.11), но всегда удовлетворяет условию

                                       .                                            (2.12)

3. Если окончательный результат измерения является функцией одной величины:

                                                         ,                                                            (2.13)

то погрешность результата

                                                         δ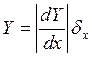.                                                       (2.14)

4. В общем случае погрешность функции нескольких величин

                                                    Y = f (x, y, ..., w),                                                     (2.15)

погрешности которых независимы и случайны, находятся по формуле

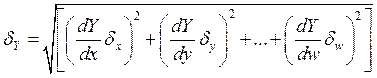                                                          (2.16)

В любом случае погрешность никогда не превышает значения

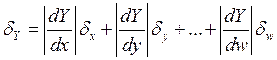                                     .                                        (2.17)      

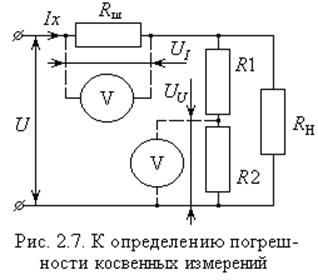
Задача: Определить величину активной мощности P постоянного тока в нагрузке R_Н с учетом инструментальной погрешности (рис. 2.7). Для измерения тока используется шунт и вольтметр, для измерения напряжения – делитель напряжения R1, R2 и тот же вольтметр. Величины R1, R2, R_ш известны. Классы точности вольтметра, шунта и делителя заданы значениями d_V, d_Ш, d_Д соответственно [9, с. 46].

Решени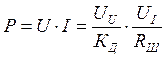е: , где .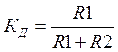

Поскольку о корреляции погрешностей используемых

приборов ничего не известно, то они складываются

средне геометрически. Вольтметр используется в обоих

измерениях и, так как его погрешность систематическая

(постоянная),  то учитывается с коэффициентом корреляции,

 равным 1. Суммарная погрешность [П 2.3]:

                                  

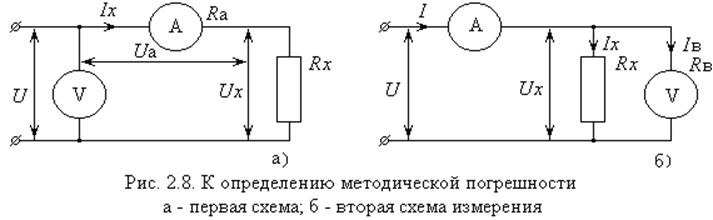
Приложение 2.1. Измерение сопротивления методом амперметра-

вольтметра. Определение методической погрешности

Метод амперметра-вольтметра  легко осуществим,  не  требует специальных приспособлений и аппаратуры. Он является особо ценным при измерении нелинейных сопротивлений, значения которых меняются в зависимости от значений протекающего по объекту измерения тока. Часто бывает необходимо измерить сопротивление в условиях рабочего режима, который иногда требует протекания по объекту измерения значительных токов.  Это делает невозможным применение других методов измерения сопротивлений, например, мостового. Метод амперметра-вольтметра широко применяется при измерении сопротивлений обмоток  электрических машин в рабочем режиме, сопротивлений электрических ламп накаливания, полупроводниковых элементов и во многих других случаях. Измерения производятся по двум схемам (рис. 2.8, а и б).

Значения сопротивлений, вычисленные по показаниям приборов R’x, для обеих схем определятся

                                                            R’x = Uв / Ia,                                                   (2.18)

где Uв, Ia - показания вольтметра и амперметра, соответственно.

Из-за влияния самих средств измерения возникает методическая погрешность. Относительная методическая погрешность определится:

- для схемы рис. 2.8, а:

                            R'x = U/Iх = (Ua + Ux)/Ix = Ua/Ix + Ux/Ix = Ra + Rx;                (2.19)

                                  ;                           (2.20)

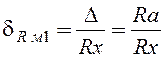                                                    .                                               (2.21)

- для схемы рис. 2.8, б: R'x = Ux/I = Ux/(Ix + Iв);                                          (2.22)

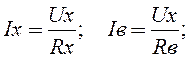                                                                                              (2.23)

Уравнение (2.22) с учетом (2.23) примет вид