Случайная величина. Дискретные, непрерывные случайные величины

II.  СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ РАСПРЕДЕЛЕНИЯ

2.1  Случайная величина

Теория вероятности не достигла бы такого расцвета и не была бы столь широко используема, если бы она занималась только случайными событиями. Вторым не менее важным объектом изучения в теории вероятности является случайная величина (с. величина).

Прежде чем дать определение с. величины, приведем некоторые сведения из функционального анализа.

Определение. Пусть (X,F) – некоторое измеримое пространство. Функция μ(А), , называется мерой, заданной на F, если выполнены следующие условия: 1) μ(А)≥0 ; 2) для любого счетного набора попарно непересекающихся множеств , таких что 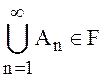, выполнено свойство счетной аддитивности (σ – аддитивности): .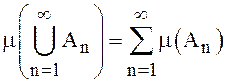

Мера называется конечной, если дополнительно выполнено условие .

Мера μ, заданная на σ – алгебре F, обладает следующими свойствами:

1. 

2.  ;

3.  ;

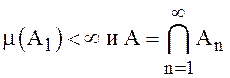4.  Если  убывающая последовательность, такая что , то .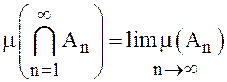

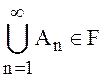Если последовательность - возрастающая и такая, что , то .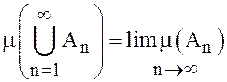

Определение. Пусть (X,F) – некоторое измеримое пространство. Вещественная функция  называется F –измеримой или просто измеримой, если 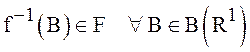, где и 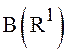  - борелевская σ – алгебра на .

  Тем самым измеримость функции означает, что прообраз любого

борелевского множества из 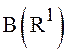 является измеримым множеством в Х (является элементом σ – алгебры F).

Перейдем теперь к определению с. величины. С точки зрения функционального анализа случайная величина представляет собой обычную числовую функцию, заданную на пространстве элементарных исходов Ω и измеримую относительно борелевской σ- алгебры 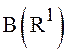  и  , B – любое борелевское множество из 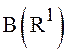. Дадим формальное определение с. величины.

Определение. Пусть (Ω,F,P) – некоторое вероятностное пространство. Случайной величиной называется измеримая функция ξ, ставящая в соответствие каждому элементарному исходу  число .

Термин «измеримая» означает, что все множества , то есть являются событиями для любого борелевского множества B из .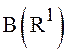

Случайные величины будем обозначать греческими буквами       и т.  д.  или большими латинскими буквами A, B, X, Y и т.д.

Напомним, что борелевские множества на прямой - это множества σ- алгебры 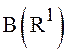, которая включает в себя все открытые и замкнутые интервалы на R, обозначают их в общем виде как .

Отметим еще, что σ- алгебра борелевских множеств 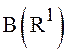 не является единственной σ- алгеброй на прямой. Ее применение в теории вероятности удобно, потому что если измеряется случайная величина ξ, то основной вопрос, интересующий экспериментатора, это вопрос о том, с какой вероятностью эта с. величина принимает то или иное свое значение, и всегда можно дать ответ на вопрос  имело ли место событие   { ξ принадлежит данному интервалу Δ }.

Поскольку σ- алгебру 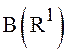 можно считать порожденной алгеброй, состоящей из полуоткрытых справа отрезков  (см. примеры 3 и 4),  то имеет смысл рассматривать события

Для краткости применяется одна из указанных форм записи. Все же остальные события вида , выражаются через выше означенные.

Итак, будем рассматривать события . Важнейшей характеристикой с. величины является ее функция распределения.

Определение. Функцией распределения (вероятностей) случайной величины ξ называется функция , значение которой в точке x равно вероятности события , то есть

                                              (2.1)

Функция распределения случайной величины есть самое полное описание случайной величины. Все, что можно сказать о случайной величине ξ, заключено в ее функции распределения . В дальнейшем, где это не будет приводить к недоразумениям, индекс ξ у функции распределения  будем опускать.

Функция распределения порождает вероятностную меру на измеримом пространстве  (R, 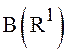)  (см. свойство F5).

Основные свойства функции распределения.

F1.

Это свойство очевидно, поскольку F(x) – вероятность.

F2. F(x) – неубывающая функция, то есть  если , то .

Результат следует из того факта, что событие  входит в событие   при условии . Тогда по свойству 3 вероятностей  или .

F3.

Событие  - невозможное событие, поэтому . Событие  - достоверное событие, поэтому .

F4. F(x) – непрерывная  слева  функция в каждой точке х.

Пусть возрастающая последовательность чисел, сходящаяся к . Докажем, что   . Рассмотрим события = {ξ<}, = {ξ<},… и . Очевидно, что , n≥1, следовательно, последовательность  монотонная и ее предел 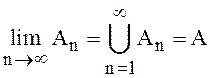. Рассмотрим,  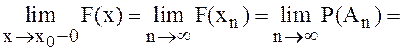|используем аксиому непрерывности А4|  .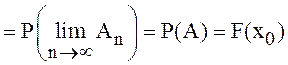

F5. . 

Событие  есть объединение двух несовместных событий  и . По свойству Р7  вероятностей из условия следует .

F6. Р{ξ≤х}=F(x+0).

По определению , где  – убывающая последовательность,. Поскольку 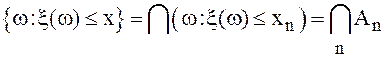, согласно  свойству непрерывности вероятности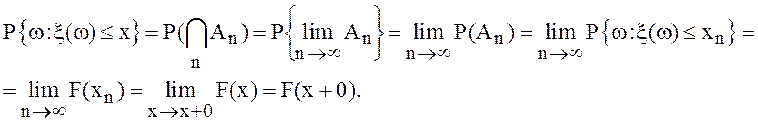

F7. Р{ξ=х}= F(x+0)- F(x).

Так как =- и  , то P=Р-Р= |следствие свойства Р 3 вероятностей |= F(x+0)- F(x).

На основании свойств F1÷F7 могут быть получены важные для практических целей результаты, а именно:

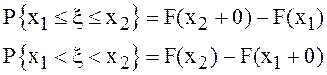
,  причем                              (2.2)

      (свойство F7).

          Докажем одно из равенств. Так как

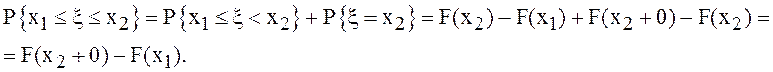
Итак, с любой случайной величиной ξ связана функция распределения F(x): неотрицательная, неубывающая, непрерывная слева функция, .

Обратное утверждение также имеет место: любая, неубывающая, непрерывная слева функция, удовлетворяющая условию , является функцией распределения некоторой случайной величины