Расчет переходного процесса классическим и оперативным методами

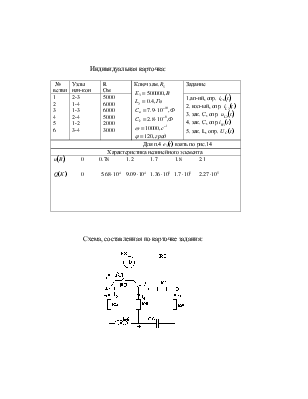
                      Индивидуальная карточка:

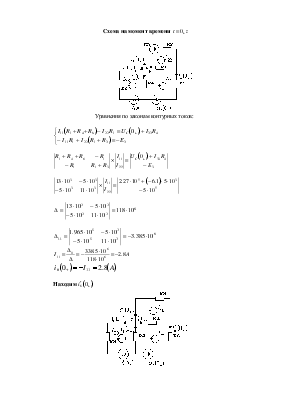
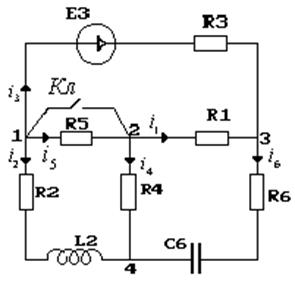
                  Схема, составленная по карточке задания:

          Переходной процесс – процесс изменения токов и напряжений в цепи, вызванный коммутацией.

           Коммутация – любое изменение параметров в цепи, включение и отключение ветвей.

Считается, что коммутация происходит мгновенно, при t=0. Основным элементом коммутации является ключ.

Начало отсчета времени переходного процесса t=0 начинается с момента коммутации. Этот момент времени непосредственно перед мгновенной коммутацией обозначается   , а сразу после мгновенной коммутации .

Переходной процесс протекает между установившимися режимами:

1) t ≤ 0 – установившийся режим до коммутации (в данной задаче – ключ разомкнут).

2) t ≥ 0 – установившийся режим после коммутации (в данной задаче – ключ замкнут).

 1) Рассчитать переходный процесс классическим методом для исходной схемы, найти .

                        Классический метод расчета.

Метод заключается в интегрировании дифференциальных уравнений, связывающих токи и напряжения цепи, в результате чего появляются постоянные, и в определении постоянных из начальных условий, вытекающих из законов коммутаций.

        Решение исходных функций записывается в виде:

                                          , где

      ,-установившееся значение исходной величины в после                         коммутационном режиме при t=∞;

      ,- общее решение обыкновенного однородного линейного дифференциального уравнения.

                         Схема, составленная по карточке задания:

                                                 Решение:

1) ;

2) Определяем принужденную составляющую , на момент времени равный t= ∞.

Схема на момент времени t= ∞:

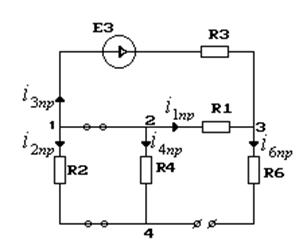
На основании данной схемы:

Поскольку при  t=∞ → индуктивность является закороткой, емкость - разрывом цепи. Из этого следует,  .

3) Определяем - решение обыкновенного однородного линейного дифференциального уравнения.

3.1. Записываем закон для цепей переменного тока на момент коммутации:

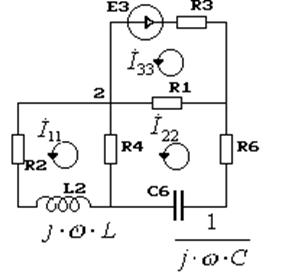
Записываем систему уравнений по методу контурных токов:

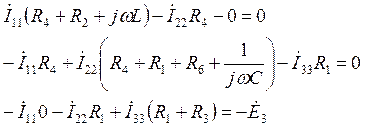
Производим замену: , тогда:

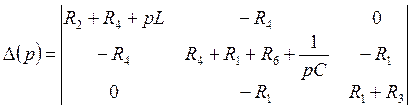- главный определитель системы.                       Решаем уравнение:

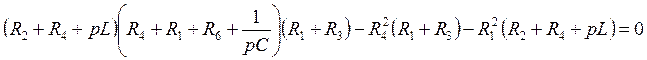
Подставляем численные значения и упрощаем:

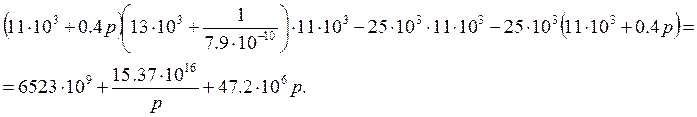
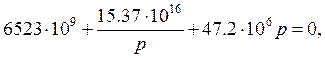
- характеристическое уравнение.

Решаем уравнение:

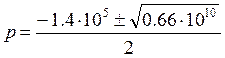
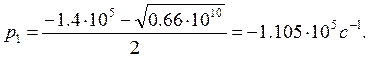
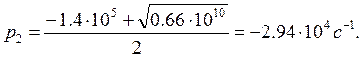
- определяют степень затухания, так как корни отрицательные, то процесс апериодический и уравнение имеет вид:

 3.2. Запишем уравнение для свободной составляющей

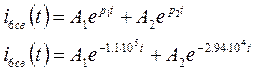
Необходимо найти постоянные интегрирования

3.3.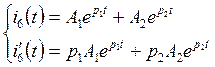 

На момент времени t=0, имеем: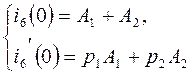

3.4. -? – зависимые начальные условия.

a) Определяем независимые начальные условия:

На основании правил коммутации:

1);

2);

          Схема на момент времени                              

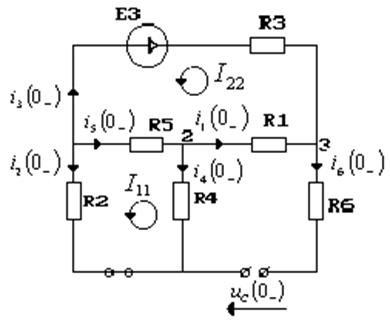
Воспользуемся методом контурных токов:

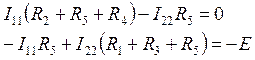
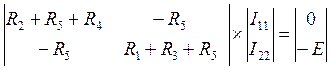
-главный определитель.

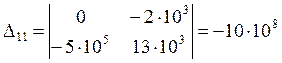
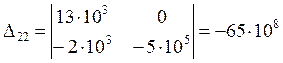
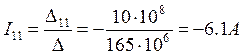
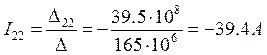
б) Определяем зависимые начальные условия

-?

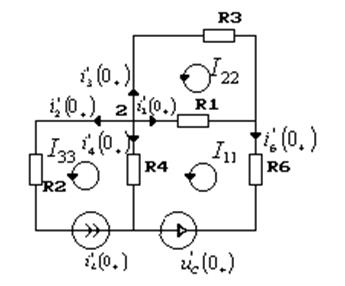
Для упрощения расчета ЗНУ справедливо на момент t=0, емкость представить в виде источника ЭДС по направлению противоположным направлению на зажимах емкости, а индуктивность источником тока по направлению совпадающим с направлением тока в ветви.

                                   Схема на момент времени :

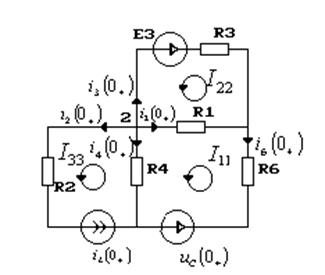
                             Уравнения по законам контурных токов:

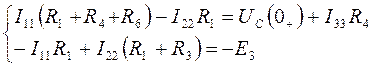
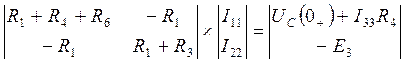
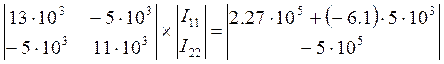
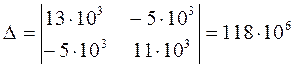
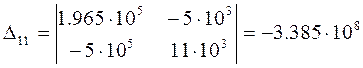
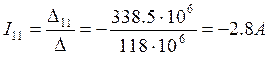
Находим

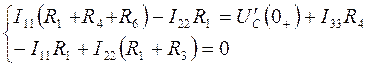
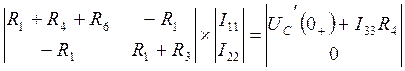
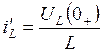
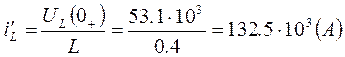
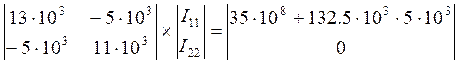
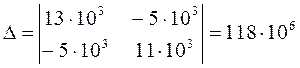
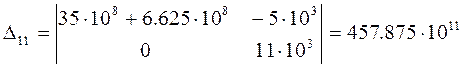
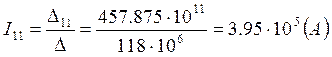
Таким образом,

3.6. Итак,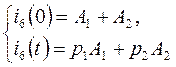 

   подставляя численные значения, получим:

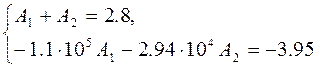
Решая систему уравнений, находим постоянные интегрирования:

,

Таким образом,

                                 Ответ: , А

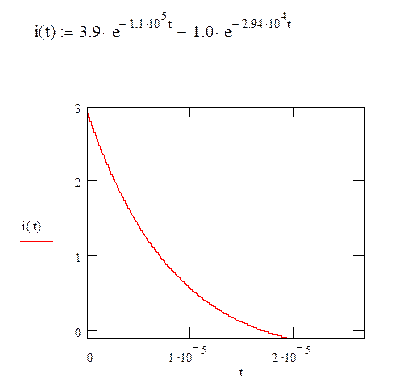
2) Рассчитать операторным методом переходный процесс для исходной схемы, определить .

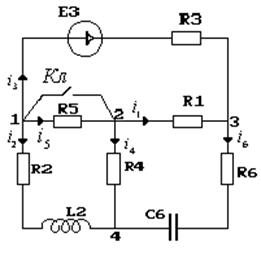
                                       Исходная схема:

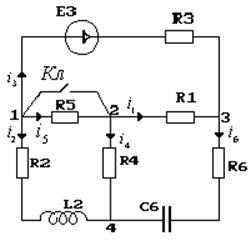
                                                         Решение.

1)Определяем независимые начальные условия.

На основании правил коммутации:

1);

2);

                                      Схема на момент времени                           

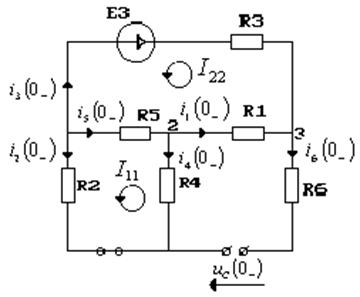
Воспользуемся методом контурных токов:

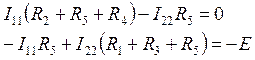
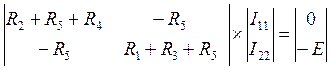
-главный определитель.

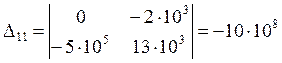
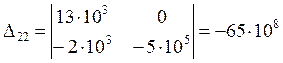
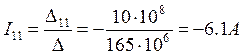
2)Переходим в область операторных изображений.

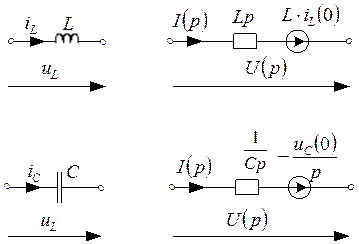
                   Схема замещения в операторной форме.

 Схема строится для после коммутационного режима.

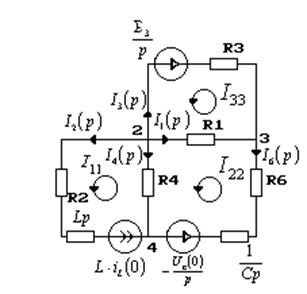
Воспользуемся методом контурных токов:

  ,

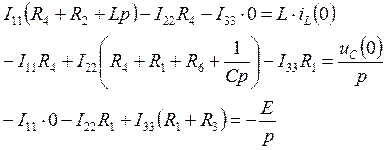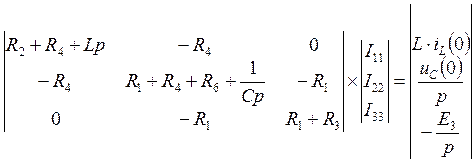
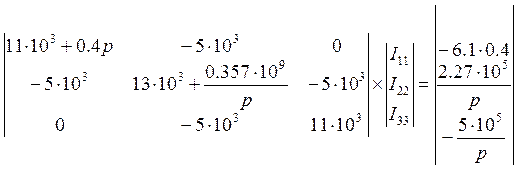
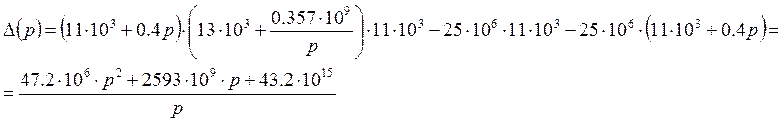
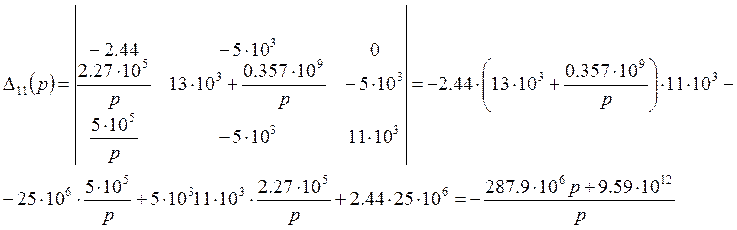
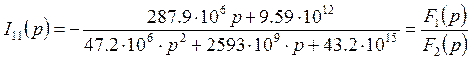
Из результата видим, что принужденная составляющая равна 0.

Для нахождения  оригинала воспользуемся теоремой разложения,определим корни знаменателя и в зависимости от корней определим оригинал.

         Решаем характеристическое уравнение  

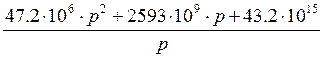=0, =0

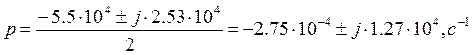 -  корни комплексно – сопряженные, процесс колебательный, имеет вид затухающая синусоида.

  ,

Согласно теореме разложения,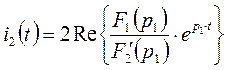  

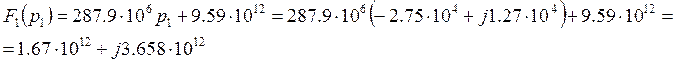
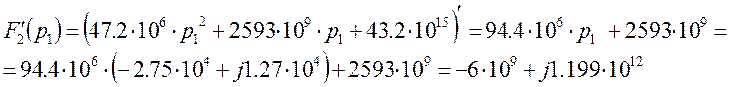
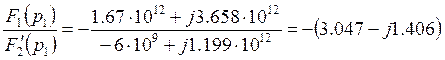
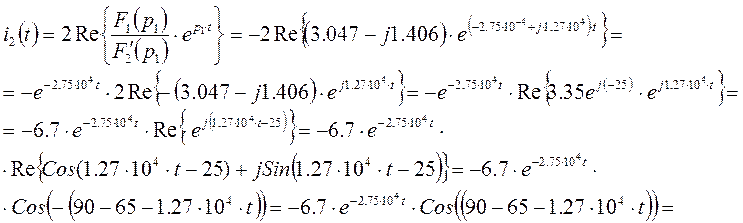
Таким образом,

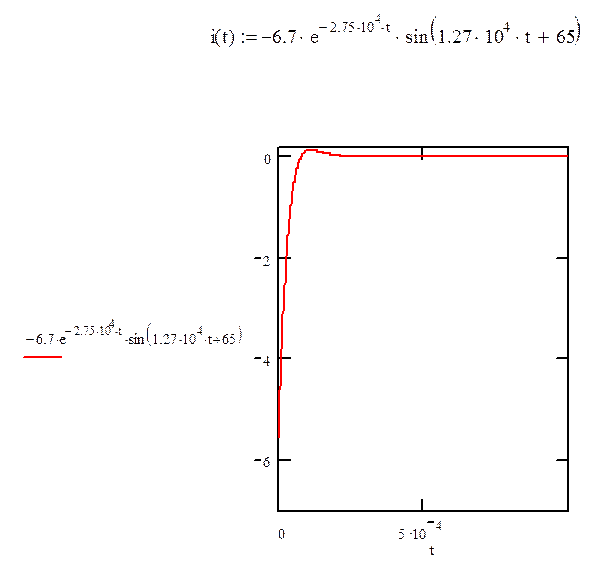
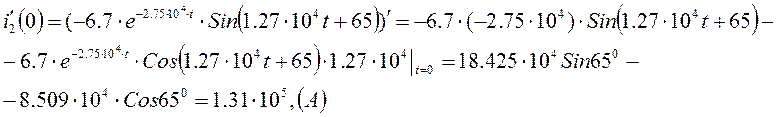            Ответ:

3)Рассчитать переходный процесс для цепи переменного тока, определить .

Для получения расчетной схемы необходимо закоротить емкость конденсатора, а источник постоянной ЭДС  - Е заменить синусоидальным источником  ,

                                     Расчетная схема: