Расчет переходных процессов в электрических цепях (R1 = 40 Ом, R6 = 30 Ом, Е4 = 200 В, L4 = 0.3 Гн)

Формируем по индивидуальной карточке исходную схему (рис№1):

Рис №1

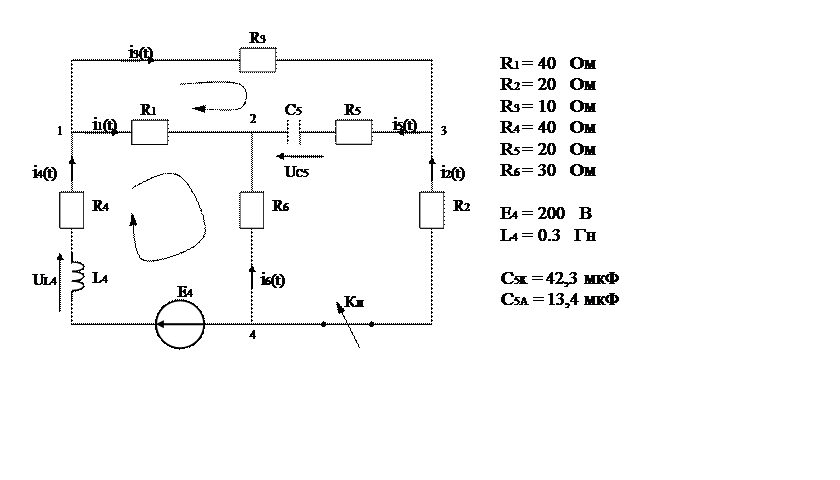
Задание№1

Рассчитать классическим методом переходный процесс для исходной схемы рис№1. Определить UL4. Процесс колебательный.

1. При переходном процессе напряжение определяется, как сумма принуждённой и свободной составляющих:

2. Определим каждую составляющую:

а) Принуждённая составляющая определяется из установившегося режима в схеме при     t→ ∞. Так как в цепь включён источник постоянной ЭДС, то напряжение на катушке в установившемся режиме равняется нулю (катушка закорачивается). Таким образом:

б) В схемах второго порядка (с двумя реактивными элементами) свободная составляющая имеет сложный вид. Для его определения составим и решим характеристическое уравнение:

           для этого введём замену:

                                              

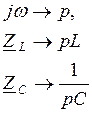
            обходя контура, составим главный определитель и приравняем его к нулю:

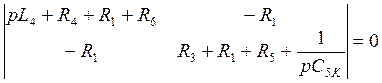
            отсюда найдём корни характеристического уравнения:

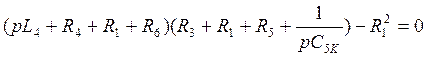
            для упрощения задачи перейдём к числам…

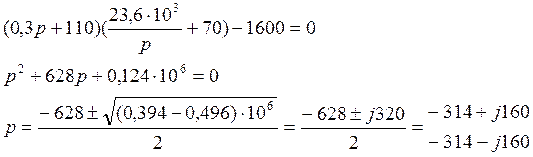
Получили два комплексно-сопряжённых корня , таким образом, вид свободной составляющей:  

3. Получили:

значения оставшихся неизвестных параметров найдём из начальных условий:

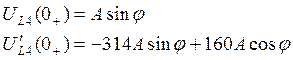
4. Воспользуемся законами коммутации:

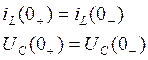
рассмотрим режим   :

так как ЭДС постоянна, то на месте катушки закоротка, конденсатора – разрыв (рис№1.2).

 

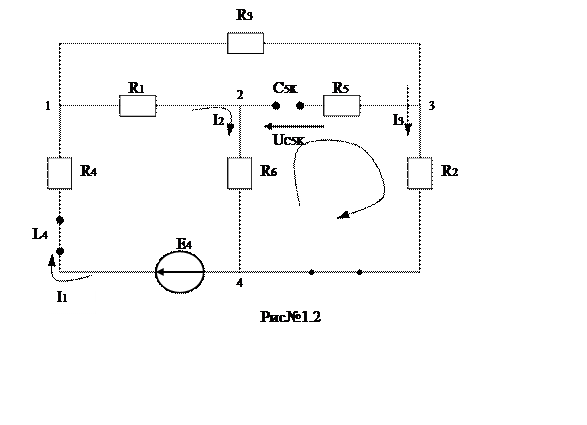
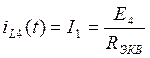
относительно ветви 4:

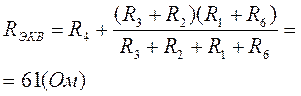
тогда искомый ток:

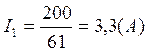
по правилу растекания найдём остальные токи:

                     

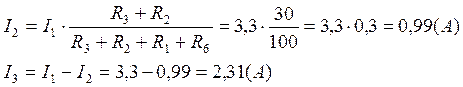
Обходя контур на рис№2, из второго закона Кирхгофа имеем:

Таким образом, мы нашли начальные условия для данной цепи:

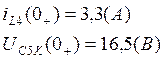
5. Теперь составим послекоммутационную схему (после размыкания ключа - рис№1.3) и систему уравнений по законам Кирхгофа.

              (*)

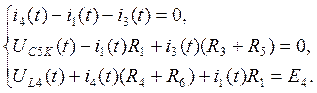
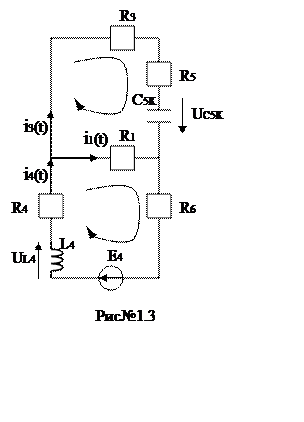перепишем полученную систему для  :

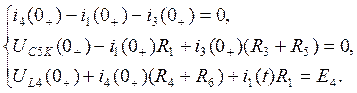
пользуясь начальными условиями, найденными в пункте 5, решим систему:

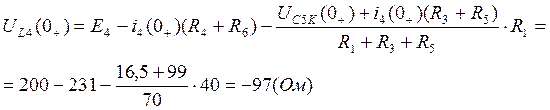
Теперь продифференцируем систему (*) и запишем при :

               

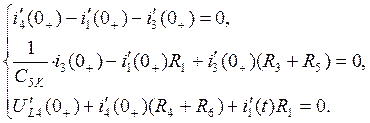
Так как    ,      то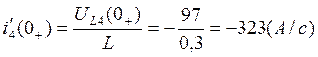     

Решая систему, получим:

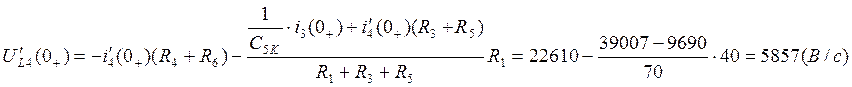
6. Теперь найдём оставшиеся неизвестные параметры  и φ:

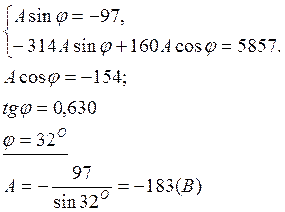
7. Получили ответ:

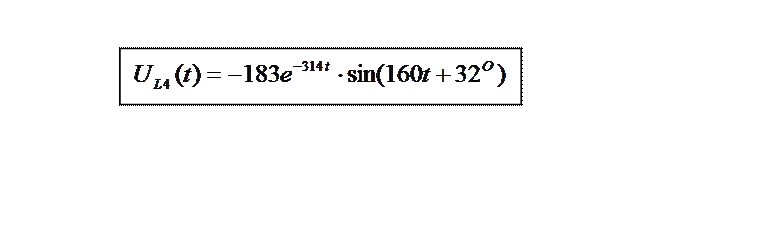
Задание№2

Рассчитать операторным методом переходный процесс для исходной схемы (рис№1). Определить iL4(t). Процесс аппериадический.

1. Для решения задачи, составим эквивалентную исходной схему замещения в операторной форме (рис№2.1):

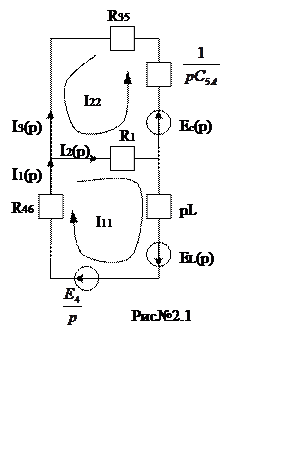Схему упростили, объединив последовательно соединённые сопротивления (далее в работе будут использоваться эти обозначения).

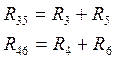
2. Теперьопределим все неизвестные параметры цепи:

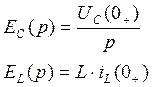
Так как схема эквивалентна схеме из задания№1, то  начальные условия совпадают с найденными ранее, таким образом имеем:

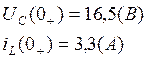
Тогда мы получаем:

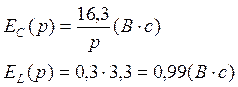
3. Составим систему уравнений по методу контурных токов:

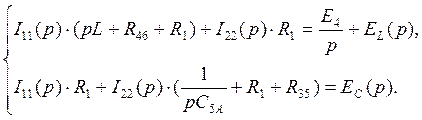
Для решения воспользуемся методом Крамера:

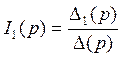
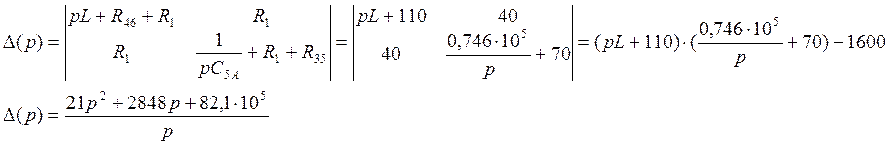
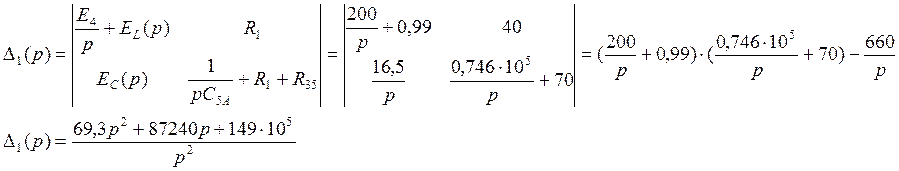
Тогда получим образ тока:

  ,     

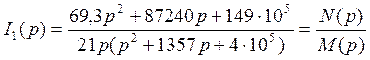4. Проанализируем это выражение и найдём его свойства:

1)  n<m;

2)  N(p), M(p) не имеют общих корней;

3)  I(p) не имеет кратных полюсов.

Значит, оригинал тока мы можем найти по формуле:

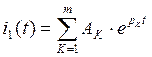   , где   pk   найдём из уравнения М(р)=0, а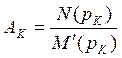

Решая уравнение М(р)=0, находим, что   ,    ,    ,

а так же   

Находим коэффициенты:

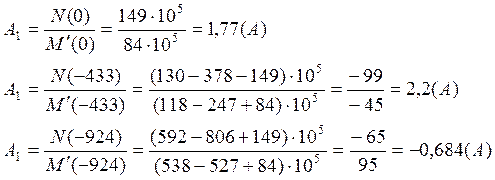
5. Таким образом, мы получили ответ:

                        

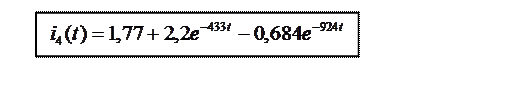
6. Произведём проверку решения для крайних значений времени:

        а) из решения:

                                 

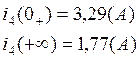
        б) из схемы (рис№1):

            в пункте 4 задания№1 мы определили, что   ,

                                 .       

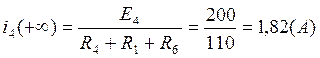Как видно, результаты совпали с небольшой погрешностью, что свидетельствует о правильности расчётов.           

7.   Для найденного тока построим график:

                              

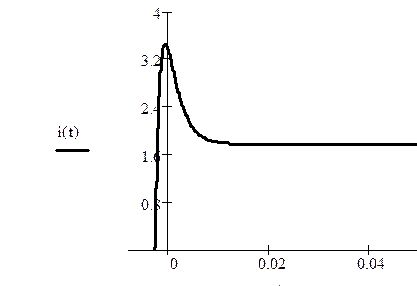
Задание№3

Рассчитать переходный процесс классическим методом. Индуктивность закорачивается, источник ЭДС  - . Определить ток iC5K(t).

Ход решения подробно описывался в задаче№1.

1.        

2. Поскольку источник ЭДС в цепи – синусоидальный, то для расчетов будем пользоваться Символическим методом:

            

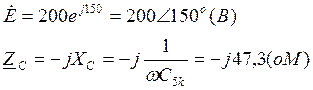
а)  t→ +∞  при этом    . Рассчитаем принуждённую составляющую тока.

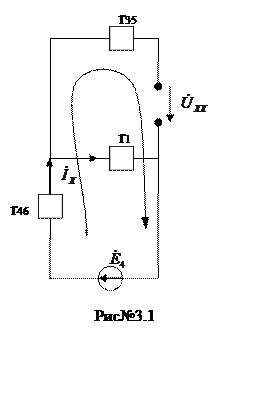Для нахождения искомого тока, воспользуемся методом эквивалентного генератора (составим схему, в которой на месте конденсатора делаем разрыв - рис№3.1).

                 

                

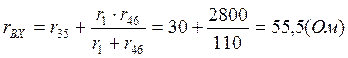
Обходя обозначенный контур, из второго закона Кирхгофа имеем:

           

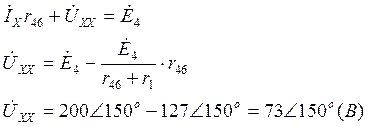
Тогда по теореме об эквивалентном генераторе получаем:

       

Перейдём к явному виду тока: 

б)     Свободна составляющая тока в цепях первого порядка (один реактивный элемент) имеет вид

,   где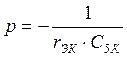      

 мы находили в части (а) пункта 2 этого задания, как входное сопротивление генератора, то есть       и тогда 

3.  Получили выражения для искомого тока:

Для нахождения параметра А, рассмотрим  решение при 

4.  Воспользуемся законом коммутации:

Рассмотрим режим   . Опять воспользуемся методом эквивалентного генератора.

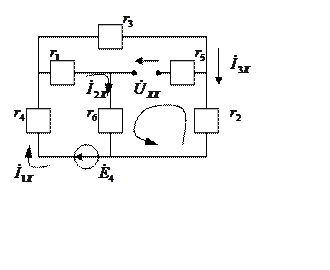Используя закон Ома в символической форме и правило растекания токов, получаем (вычисления проводим аналогично пункту 4 задания№1:  ):

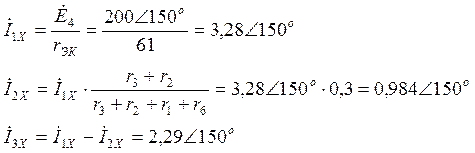
Чтобы рассчитать входное сопротивление генератора необходимо произвести преобразование треугольника сопротивлений в звезду сопротивлений:

  

   

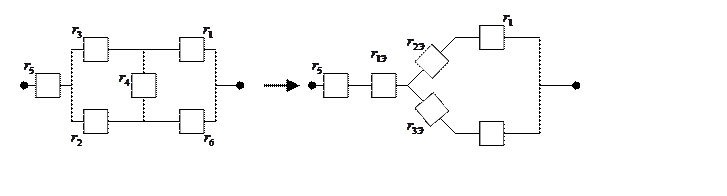
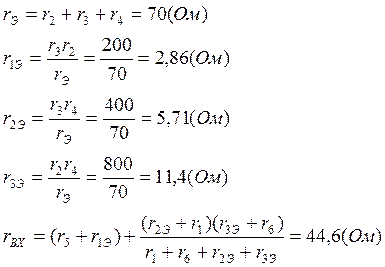
По теореме об эквивалентном генераторе получаем:

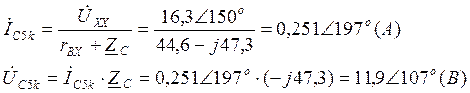
Перейдём к явному виду.

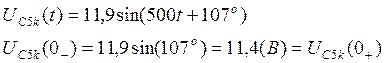
5. Теперь составим послекоммутационную схему (после размыкания ключа - рис№3.2) и систему уравнений по законам Кирхгофа.

            

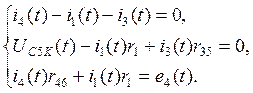
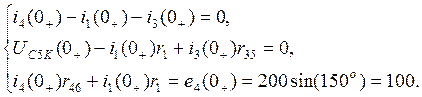
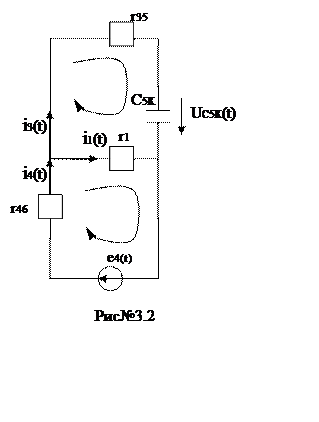Подставляя известные начальные условия, найденные ранее, получаем:

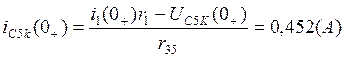
7.  Теперь найдём оставшийся неизвестный параметр :

                           

8.  Получили ответ:

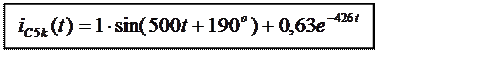
Задание№4

Рассчитать переходный процесс с помощью интеграла Дюамеля. Индуктивность закорачивается. Определить iR1(t). Процесс колебательный. График напряжения источника ЭДС представлен на рис№4.1.

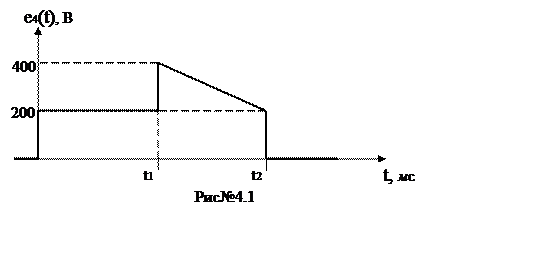Таким образом, аналитическое выражение для источника ЭДС имеет вид: