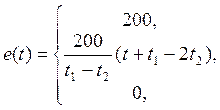
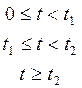
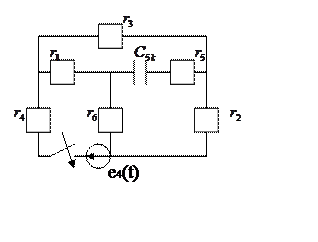
Электротехника \ Теоретические основы электротехники

Расчет переходных процессов в электрических цепях (R1 = 40 Ом, R6 = 30 Ом, Е4 = 200 В, L4 = 0.3 Гн), страница 2

1. Составим схему для данного задания. Ключ помещается в ветвь с ЭДС и включает её в цепь после коммутации. Интеграл Дюамеля имеет вид:

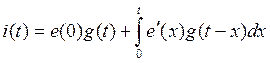, где

g(t) – переходная функция (переходная характеристика) тока, которая равна току в цепи, при ее включении на единичный скачок напряжения 1(t).

То есть, в нашем случае:

2. Определим каждую составляющую:

а) принуждённую

при на месте конденсатора имеем разрыв. Аналогичная схема рассчитывалась в пункте 4 задания№1, потому . тогда ток найдём следующим образом.

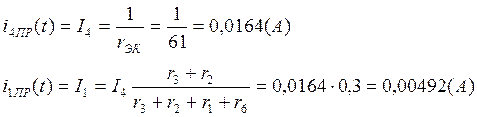
б) свободную

цепь первого порядка.

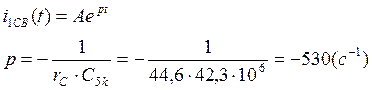, для аналогичной схемы общее сопротивление относительно конденсатора мы уже находили в пункте 4 задания№3, как !!!

Тогда, имеем:

3. Таким образом, получили:

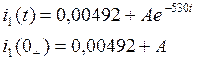
4. Для нахождения параметра А, воспользуемся начальными условиями и законами коммутации:

Так как цепь до коммутации была отключена от источника ЭДС, и конденсатор считается идеальным, то из второго закона коммутации имеем:

Это означает, что в начальный момент времени на месте ёмкости в цепи образуется закоротка (рис№4.2).

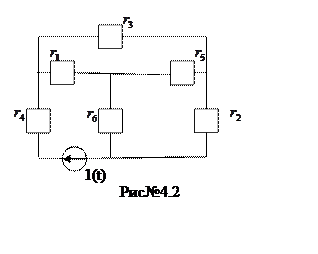
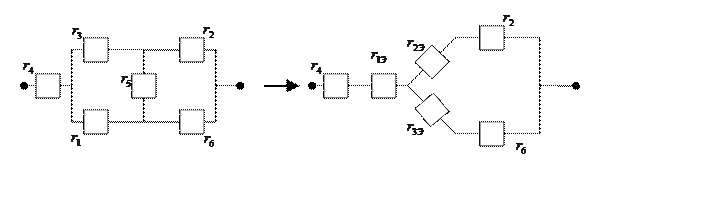
Найдём общее сопротивление относительно r4, для этого преобразуем треугольник сопротивлений в звезду:

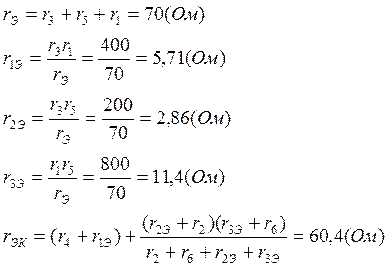
Теперь рассчитаем токи

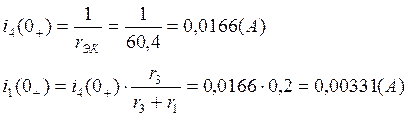
Тогда А = 0,00331 - 0,00492 = - 0,00161 (А)

5. В конечном итоге запишем переходную функцию и другие необходимые параметры:

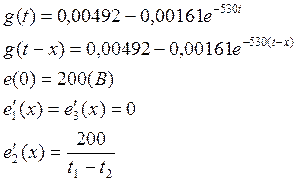
6. Запишеминтеграл Дюамеля для каждого из трёх участков графика источника ЭДС:

а)

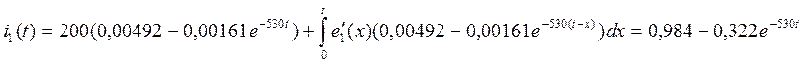
б)

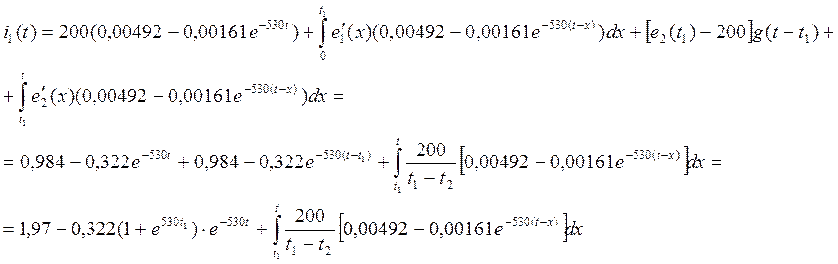
в)

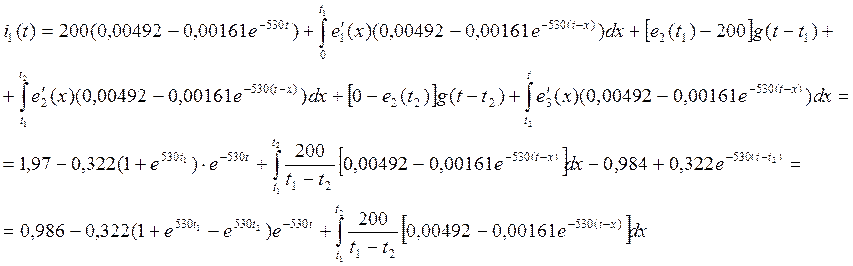
Задание№5

Рассчитать переходный процесс в нелинейной электрической цепи. Индуктивность закорачивается. Определить UC(t).

Кулон-Вольтная характеристика для нелинейного конденсатора представлена на рис№5.1.

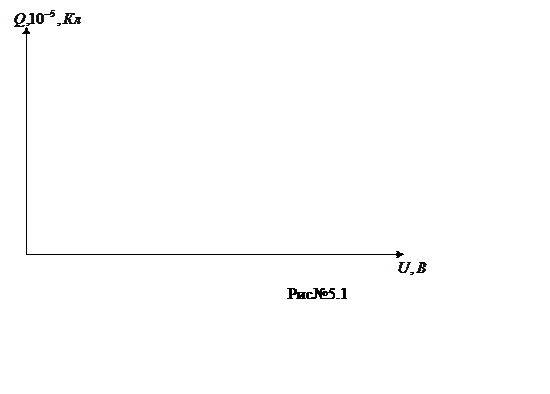
Масштабы для осей:

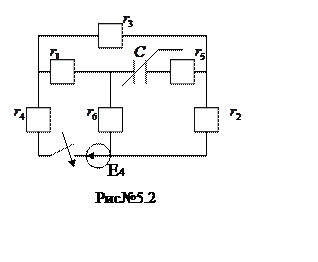
Схема для данного задания

представлена на рис№5.2

Ёмкость конденсатора связана с зарядом и напряжением следующей формулой: 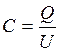. Нелинейную Кулон-Вольтную зависимость аппроксимируем двумя прямыми. На месте перегиба функции они пересекаются в точке .

1. При переходном процессе напряжение на конденсаторе складывается из свободной и принуждённой составляющих.

2. Найдём каждую составляющую:

а) Принуждённая

Так как ЭДС постоянна, то в установившемся режиме работы цепи на месте конденсатора образуется разрыв. Получаем схему аналогичную изображённой на рис№1.2 из пункта 4 задания№1 (с теми же параметрами). Откуда получаем:

б) Свободная составляющая для схемы первого порядка имеет вид:

, где τ - постоянная времени, которая имеет размерность времени и может быть определена как время, в течение которого свободная составляющая уменьшается в eраз по сравнению со своим начальным значением. Она связана с ёмкостью следующим выражением:

Из графика найдём два значения ёмкости (по двум прямым), как отношение

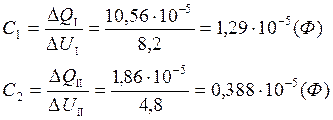тогда получим 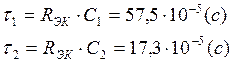, где

общее сопротивление относительно конденсатора: (мы уже находили в пункте 4 задания№3, как ).

3. Тогда для двух промежутков запишем решение:

Ι ,

ΙΙ

Время определим по формуле: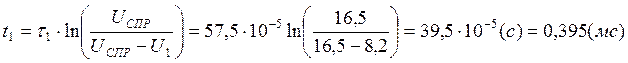

3. Определим параметры А.

так как цепь до коммутации была отключена от источника ЭДС, то конденсатор в начальный момент времени был незаряжен. То есть . Подставив это начальное условие в решение Ι, получим:

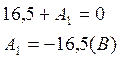
Воспользуемся известным значением напряжения , и найдём:

ΙΙ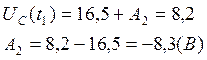

4. Получили решение:

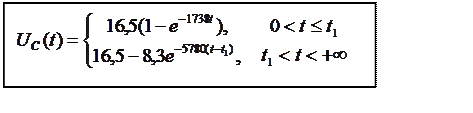
5. Для найденного решения построим график:

Масштабы по осям:

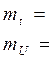
Результаты расчетов п. 1 ¸ 5 занесём в таблицу

*1,2- Классический и операторный методы*										= 16,5 В					= 3,3 А
Апериодический процесс
b		q						f(0)			f ¢(0)
—		—		—		—		—			—		—			—		—
Колебательный процесс
b		q		b				f(0)			f ¢(0)					А		y
628		0,124Е6		314		160		-97			5857		0			-183		32º
*3. Классический метод*														*4. Интеграл Дюамеля*
	j		A		p		f(0)										А		р
—	190º		1		-426		11,4		0,452			0,63		0,00492			-0,00161		-530
*5. Расчёт переходного процесса в цепи с нелинейным конденсатором*
				t=		0
44,6				f(t)=		0		8,2