Расчет переходных процессов в электрических цепях (R1 = 40 Ом, R6 = 20 Ом, Е1 = 5000 В, L4 = 2.0 Гн)

Министерство образования Российской Федерации

Кафедра Теоретических Основ Электротехники

Расчетно-графическое задание по курсу ТОЭ

Расчёт переходных процессов в электрических  цепях

Вариант №

Группа:               РФ1-32

Студент:              Эпов В.С.

Преподаватель:   Тропин В. А.

Отметка о защите

Дата защиты       «__»_________ 2005 г.

Новосибирск

2005

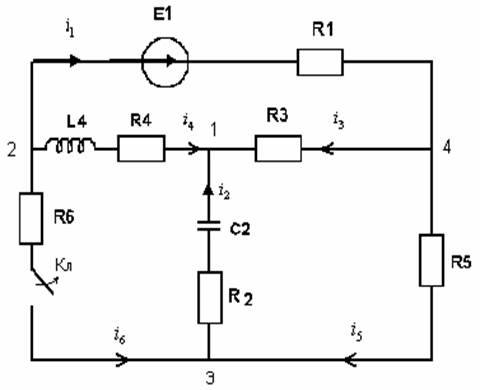                                                                                                                      Дано:

            R₁ = 40 Ом                               R₂ = 40 Ом

          R₃ = 50 Ом                               R₄ = 20 Ом                               R₅ = 40 Ом                                  R₆ = 20 Ом

E₁  = 5000 В

L₄  = 2.0 Гн

C_2k = 1.35*10^-4 Ф

C_4а = 3.17*10^-5 Ф

w  = 100 с^-1

j   = 330°

1)  Расчёт классическим методом :

 

Общая форма записи :

a)  определяем принуждающую составляющую

т.к. , то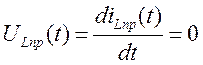  

 

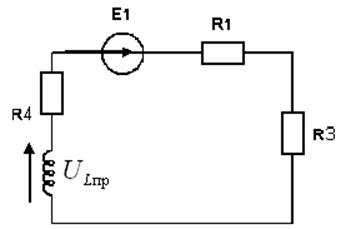b)  определяем свободную составляющую

·  Определяем КХУ:  через

 

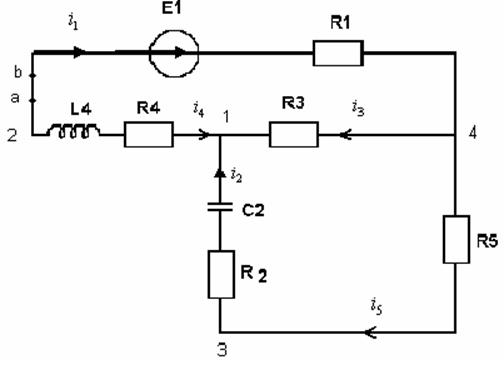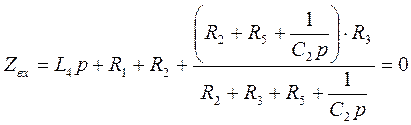 , где 

Подставляем числовые значения, и приводим уравнение к виду

           - находим корни данного уравнения

                           

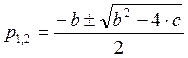
                                         Два отрицательных корня:

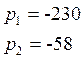                  -    процесс апериодический.

       У нас уравнение вида :

·  Определяем ННУ:

 

                                                                                                           

 

 

· 

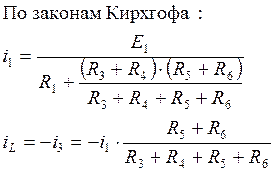
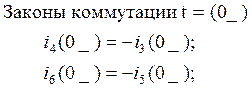
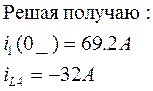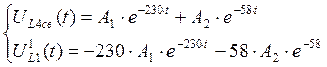
при t = 0

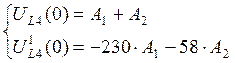
·  определяем зависимые начальные условия (ЗНУ):  

a) 

 

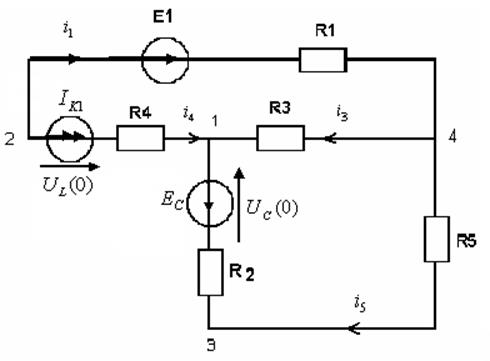                                                                                                                        Расчёт ведем как при  

                                                                                                                          постоянном токе

 

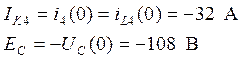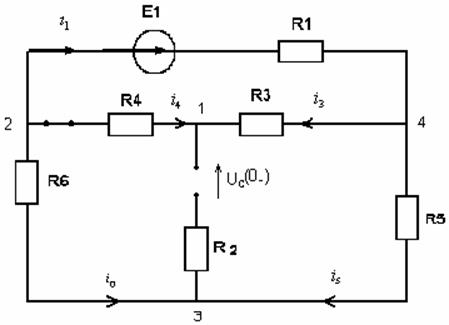
По законам Кирхгофа:

                   

;          

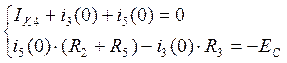
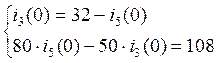
b)  Определим

        Определяем неизвестные составляющие:                                   

 

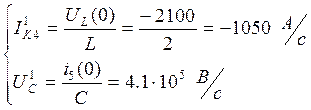По законам Кирхгофа:

                 

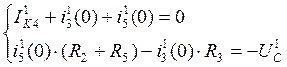
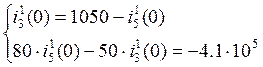
·  Произведем расчёт  и

                    

                                                    

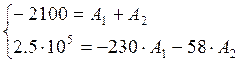
Таким образом:

                                                                                                               

2)  Расчёт операторным методом:

 

·  определим ННУ:

из предыдущего пункта задания

            

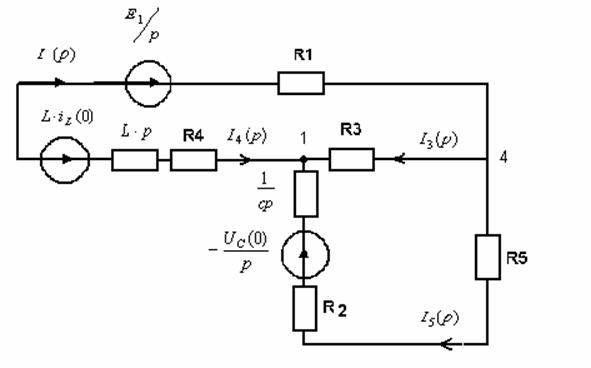
·  построим операторную схему замещения для

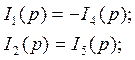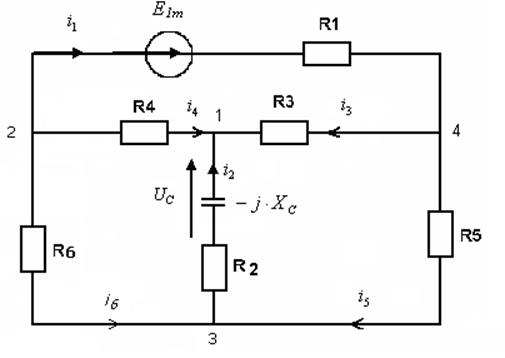
·  методом контурных токов составим уравнения:

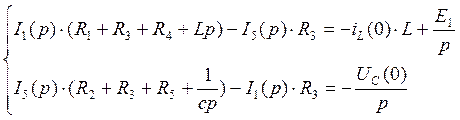
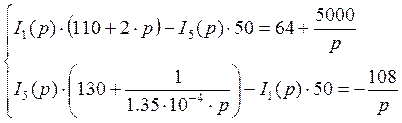
 Преобразуя данную систему и упрощая, мы получим:

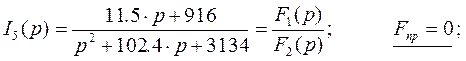
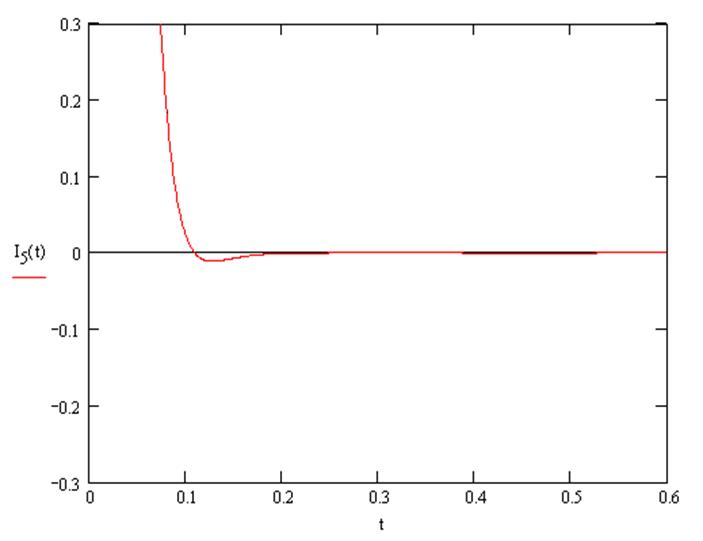
·  используя теорему разложения, определяем ток  (от операторной формы к временной форме)

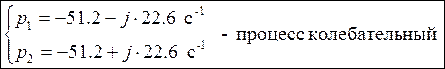
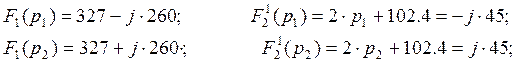
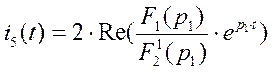
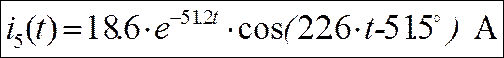
3)  Расчёт классический метод для синусоидального источника:

 

· 

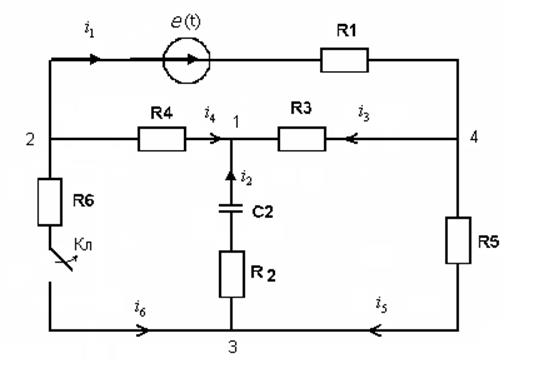
·  определим принуждающую составляющую при

 

 

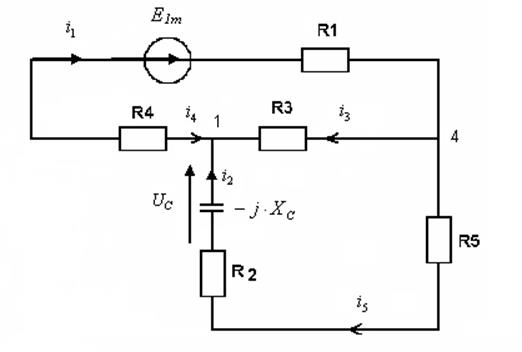
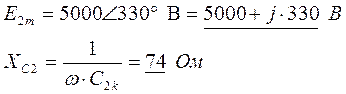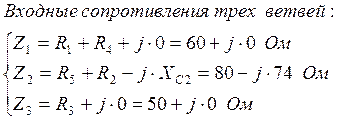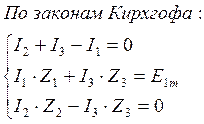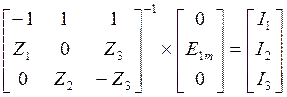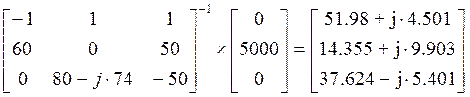Переходим к мгновенным значениям:

·  определяем

Составляем характеристические уравнения () и определяем КХУ через

                         

        

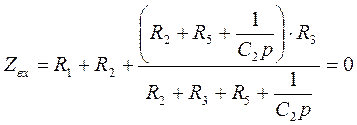
С другой стороны 

при t = 0 : 

·  определяем зависимые начальные условия (ЗНУ):

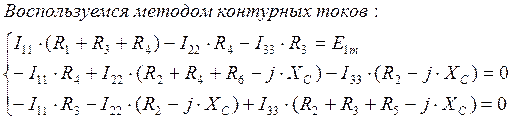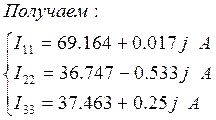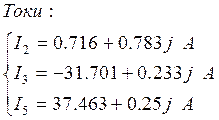Переходя к мгновенному значению и при t = 0, мы получим:

Отсюда находим :

Таким образом:

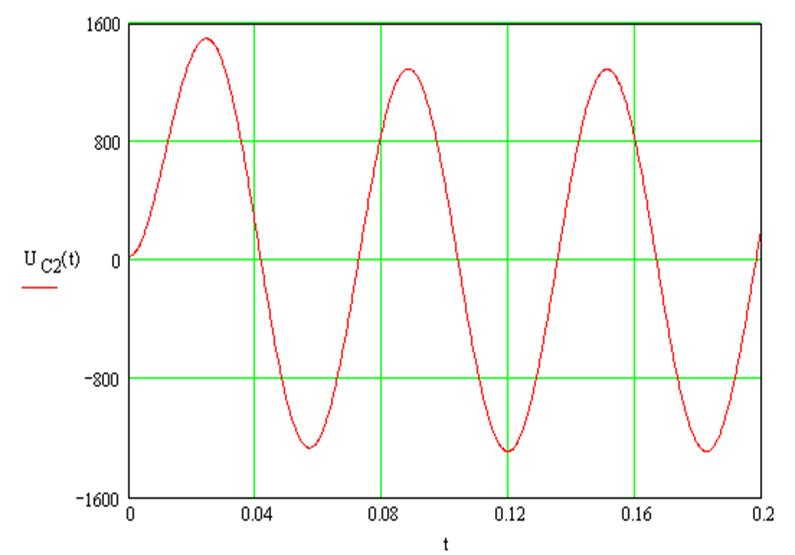
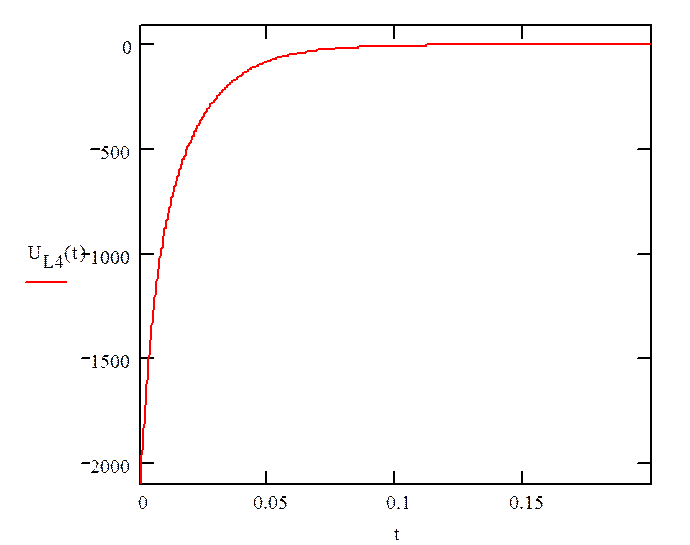
4)  Расчёт цепи с помощью интеграла Дюамеля:

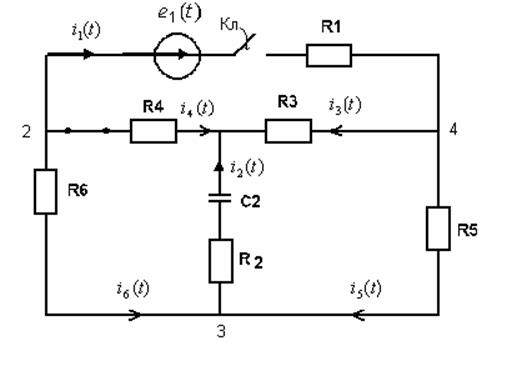
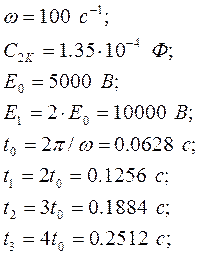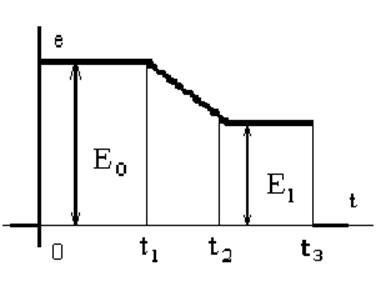
Классическим методом определяем  при

·  определяем  при

Т. к. конденсатор будет являться разрывом, то ток будет

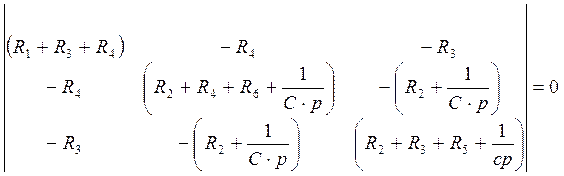·  определяем

Пользуясь методом

   контурных токов:

Подставляя значения, получаю уравнение:

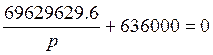    Þ     

ü  Определяем ЗНУ: ()

в момент коммутации при , ключ замкнут

  

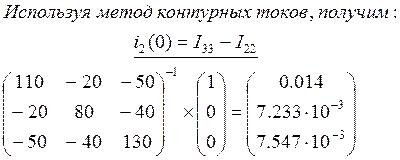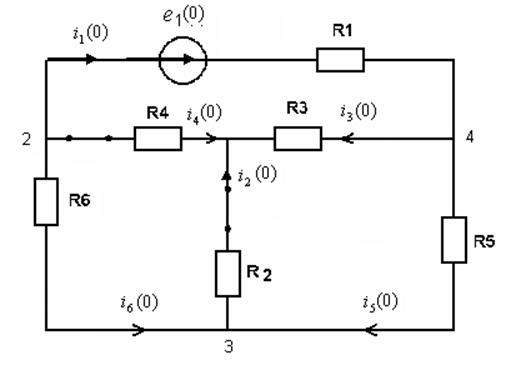
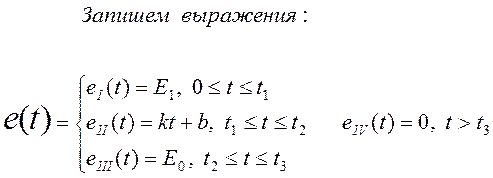
Запишем выражение для тока  на каждом участке действия ЭДС:

 

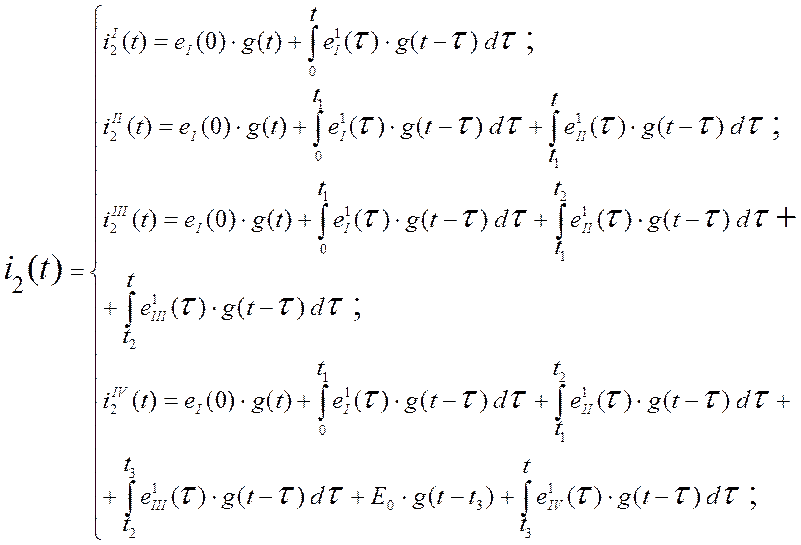
  Определяем все составляющие, входящие в :

              

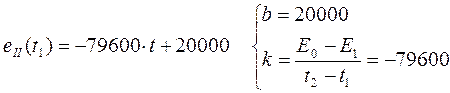
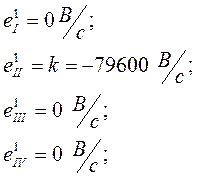
Записываем решение:

 

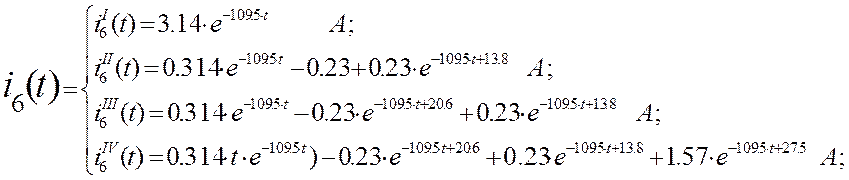
5)  Метод кусочно-линейной аппроксимации:

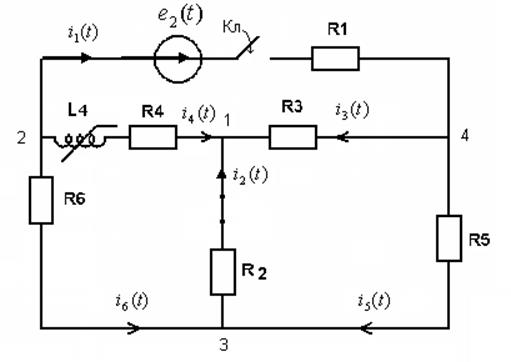
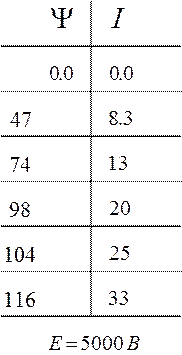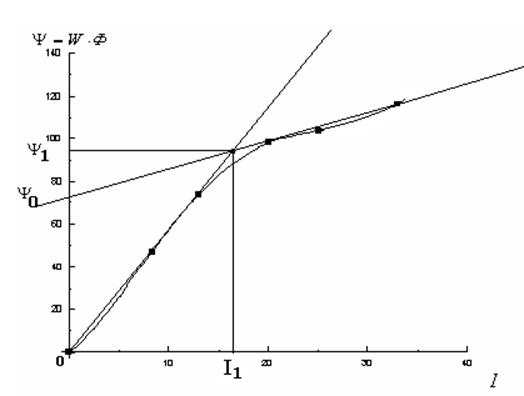
·  определим  (относительно нелинейного элемента):

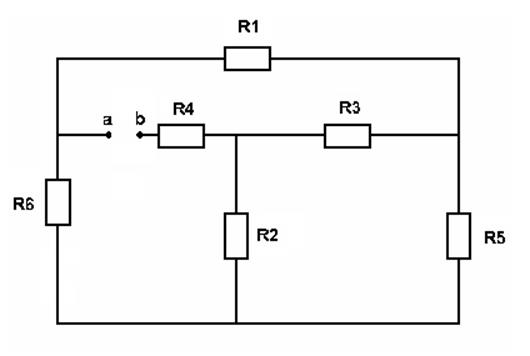
ü  Преобразуем:

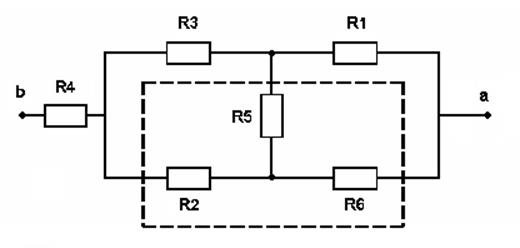
ü  Преобразуем :

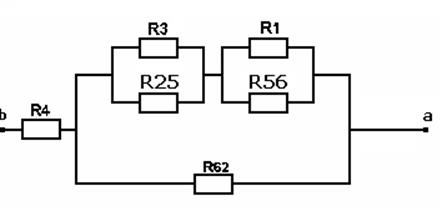
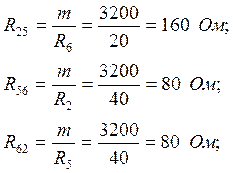
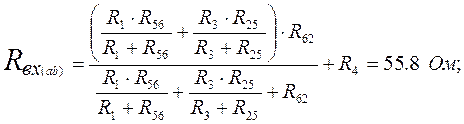
·  определим составляющие :

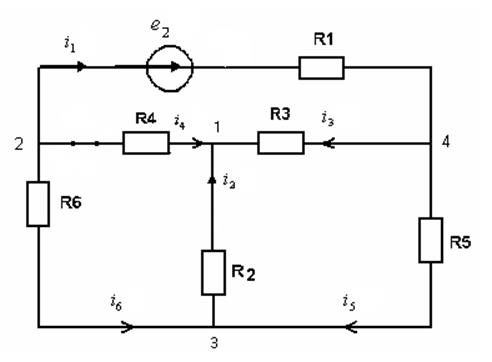при

Используем метод контурных токов:

           

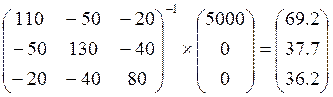
при t = 0       

Из формулы: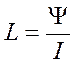           

1)  I участок:       

             

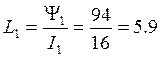
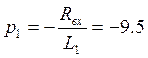
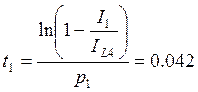
Получаем:

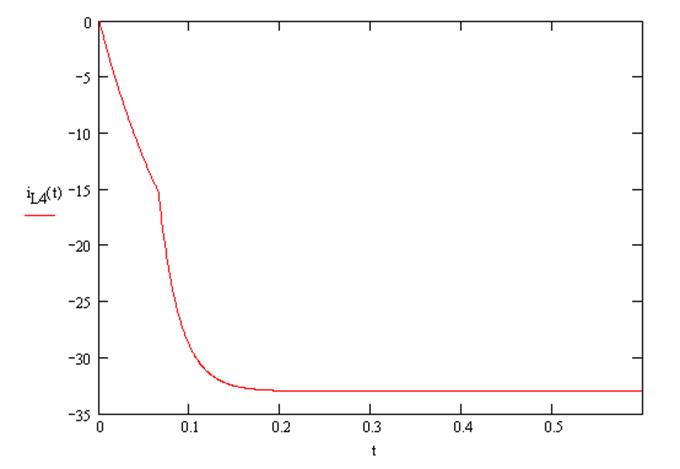
2)  II участок:       

где А₂ определяем через 1 условие t=t₁ :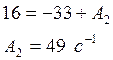  

   

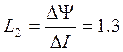
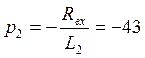
Получаем: