Расчет переходного процесса классическим и оперативным методами, страница 2

                             

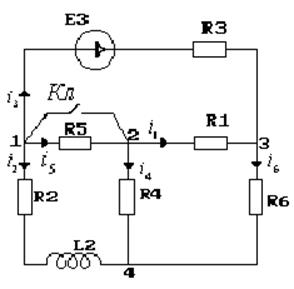
                                                Решение.

1)Определяем принужденную составляющую на момент времени t=∞.

                                         Схема на момент времени t=∞.

                                

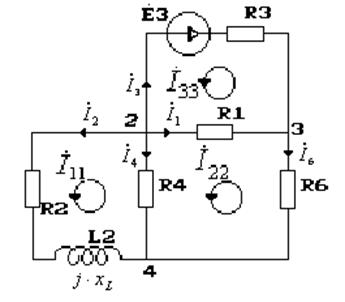
Методом контурных токов рассчитаем комплексы токов.

 

; 

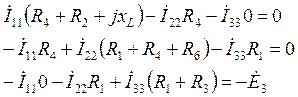
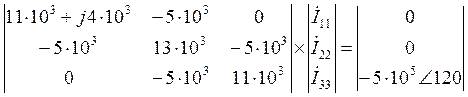
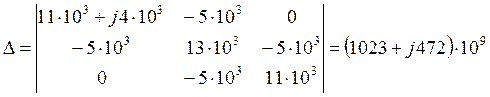
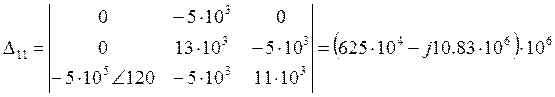
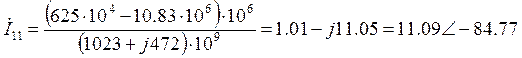
Таким образом,

2) Запишем общий вид уравнения  

                                                        

 Определяем - определяется решением однородного дифференциального уравнения первого порядка.

Уравнение имеет вид , где A – постоянная интегрирования цепи,

                                                                        p – корень характеристического уравнения.

Составляем характеристическое уравнение на момент времени t=0

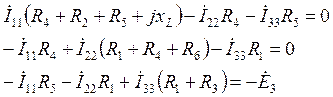,    jω→p

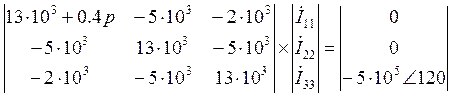
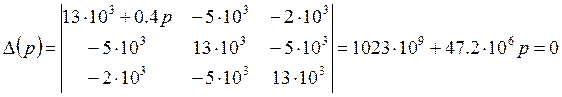
Решая уравнения, получаем 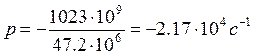 - определяет степень затухания цепи, видно, что процесс апериодический.

Находим A:

Рассматриваем уравнение на момент времени t=0

3)Определяем начальные условия.

Независимые начальные условия:

согласно законам коммутации,  

                                         Схема на момент времени

                                       

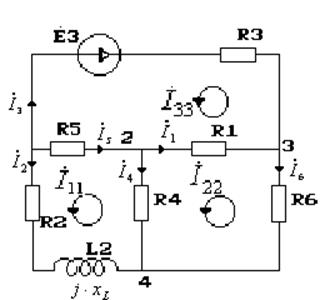
Методом контурных токов рассчитаем комплексы токов.

 

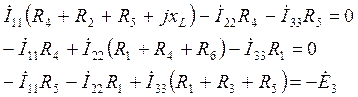
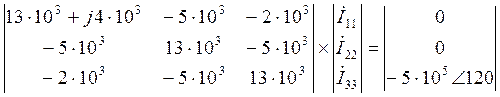
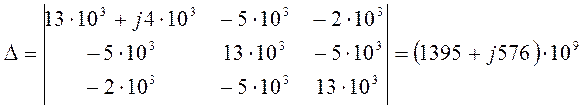
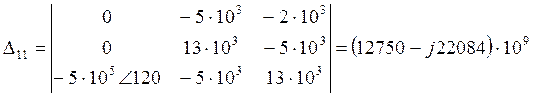
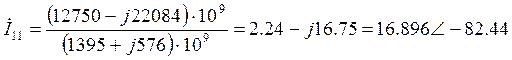
4) Таким образом,

, ,

Уравнение для имеет вид .

Поскольку , то

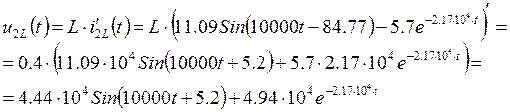
                 Ответ:

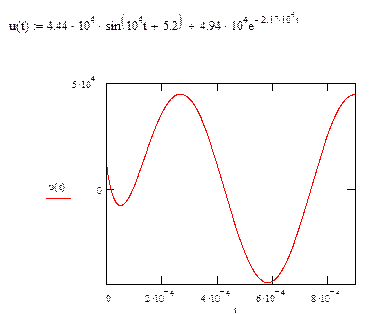
4) Рассчитать переходный процесс с помощью интеграла Дюамеля, определить ток .

Для получения расчетной схемы ключ помещаем в ветвь с источником ЭДС, который должен включать источник в схему после коммутации. Реактивный элемент С закорачиваем.      

                                      Исходная схема:     

                                                  

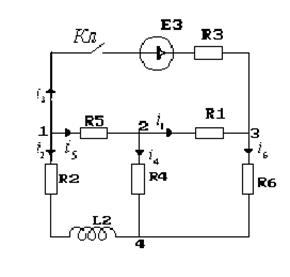
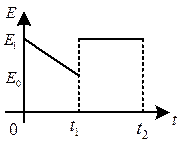
                                                       Решение.        

Два условия применимые к данной задаче:

1)Цепь должна быть пассивной;

2)Входная функция должна быть определена на интервале;

позволяют рассчитать переходной процесс интегралом Дюамеля.

Входная функция имеет сложный характер.

1)Вид входной функции на интервалах:

                

  

  

 ,     

                             => 

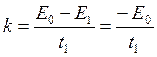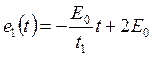
Таким образом,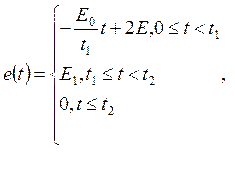

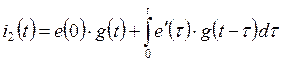 - интеграл Дюамеля в общей форме.

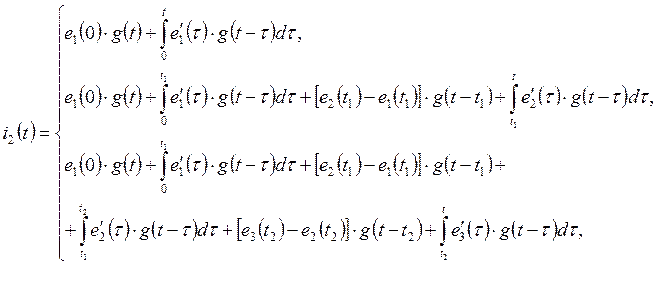
Необходимо определить , , ,,

                                           .

2)  - переходная проводимость.

Переходная проводимость равна численно искомому току при включении цепи на ЭДС равной 1В.

   Определим операторным методом .

2.1. Начальные независимее условия.

Согласно правилам коммутации:

           

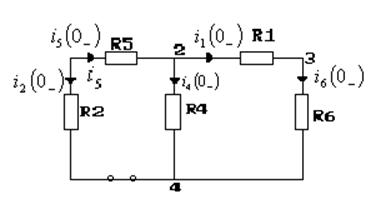
                               Цепь на момент времени :

Индуктивность – закоротка. Поскольку при  источникнапряжения отсутствует, то

                     

2.2. Переходим в область операторных значений:

                                               

        Схема замещения в операторной форме. Схема строится для послеком-го режима.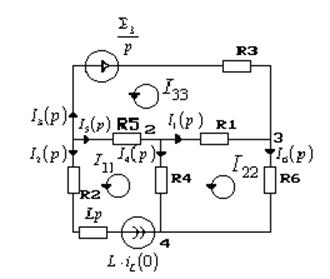  

Воспользуемся методом контурных токов:

  ,

 

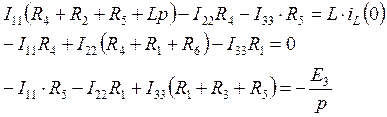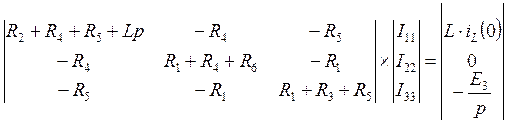
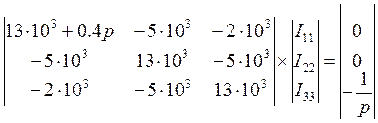
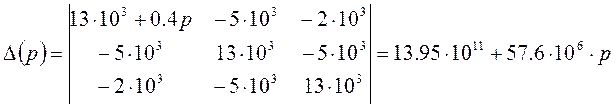
- характеристическое уравнение

=0   =>  - корень действительный отрицательный,

процесс апериодический.

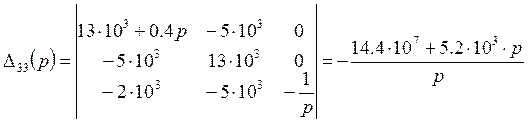
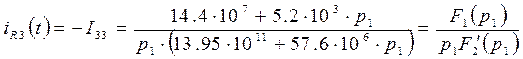
Найдем оригинал по изображению, воспользовавшись теоремой разложения.

Так как корни: равный 0 и действительный отрицательный, то