Природа процессов метрологического старения средств измерений, страница 3

Это приводит к тому, что при эксплуатации наиболее веро­ятны выходы фактической погрешности СИ за нормируемые пределы ±gкл именно в конце диапазона. Для доказательства этого были собраны данные по ежегодным поверкам

лабораторных аналоговых электромеханических приборов 33 раз­личных типов классов точности 0,5—0,2—0,1, поверяемых в те­чение 10—12 лет на поверочной установке с полуавтоматическим потенциометром типа Р2.

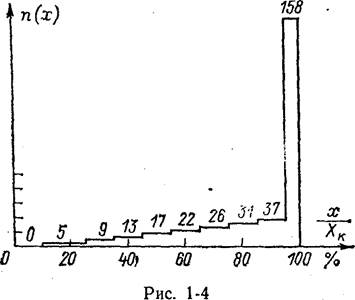
Полученная гистограмма 318 случаев выхода фактической погрешности за нормируемые границы представлена на рис. 1-4, Из нее следует, что в пределах

от 0 до 10 % длины шкалы приборов выхода погрешности за нормируемые пределы вообще не встречалось. В пределах от 10 до 95 % длины шкалы ча­стота выхода плавно возрастает по закону п(х) = ax^1,3, но мак­симальная доля выхода погрешности за нормируемые пределы, равная 158/318 » 50 %, приходится на самый конец шкалы.

Описание динамики погрешности средств измерений линейной математической моделью

Простейшая линейная модель возрастания во времени погрешности средств измерений

Изучение и описание любого физического явления сводится в конечном итоге к нахождению достаточно адекватной математической модели этого явления. Изучение заканчивается, когда модель получает удобный для практики компактный вид, например S=gt²/2 или I=U/R, и на долгий период без изменений служит инструментом инженерной деятельности. Но главным критерием пригодности модели является ее адекватность описываемому явлению. Если же такая адекватность не годится, то последующие исследователи вынуждены искать другие, более адекватные модели.

Так, во многих работах теоретический анализ изменения погрешности СИ во время эксплуатации проводится на основе представления этого процесса как стационарного случайного процесса Y(t) (рис. 2-1, а) с некоторым постоянным законом распределения, а задача анализа сводится к отысканию вида этого закона распределения. При такой постановке задачи метрологически исправное состояние СИ сохраняется до тех пор, пока мгновенные значения случайного процесса Y(t) находятся в пределах интервала [-Y_кл, +Y_кл] , где Y_кл – предел допускаемых погрешностей СИ, нормированный в соответствии с его классом точности. А выход случайного процесса Y(t) за эти пределы при t=t_отк, как это показано на рис. 2-1, а, фиксируется как метрологический отказ.

Неадекватность такой модели процесса изменения погрешности СИ во времени очевидна. Действительно, при такой модели вероятность выхода случайного процесса за границы +-Y_кл одинакова как в начальный момент эксплуатации, так и через 1 год или 10 лет. В действительности же вследствие непрерывного возрастания погрешности эта вероятность достаточно мала на протяжении первого года эксплуатации и становится существенно больше через несколько лет.

Поэтому в качестве простейшей модели прогрессирующей погрешности рассматривается нестационарный случайный процесс с постоянным во времени значением дисперсии  и линейно нарастающим текущим математическим ожиданием   - рис. 2-1,б. Эта же модель сейчас использована в ГОСТ8.009 – 84 [6, с. 60], где нестационарность отнесена лишь к систематической погрешности.

В этом случае наступление метрологического отказа в момент t_отк также соответствует точке первого пересечения случайным процессом Y(t) границ +-Y_кл. Однако если рассматривать совокупность однотипных СИ, случайные процессы возрастания прогрессирующей погрешности которых имеют совпадающие значения дисперсии  , скорости   и начального значения  математического ожидания, то для такой совокупности отказы будут наступать в разные моменты времени. Распределение этих моментов времени будет характеризоваться кривой распределения плотности вероятности 1 (рис. 2-1, б), которая в некотором масштабе приблизительно повторяет кривую распределения 2 случайной составляющей погрешности этих СИ.