|
I11 = Iк = 5 А.
Контурный ток I33 также известен, поскольку он совпадает по направлению и равен заданному току I5
I33 = I5 = 5 А.
Считая направление обхода контуров совпадающими с направлениями контурных токов, получим систему:
I11 R2 + I22 (R1 + R2 + R3 + R4) – I33R4 = –E, (для контура
a-b-c-d-a)
– I22 R4 + I33 R4 = E . (для контура d-c-d)
С учетом того что
I11 = I33 = 5 А,
система уравнений по методу контурных токов принимает следующий цифровой вид:
5 + 3I22 – 5 = -Е,
-I22×1 + 5 = Е.
Из решения системы следует:
Е = 6,67 В, I22= –1,67 А.
Реальные токи в ветвях цепи определяются как алгебраическая сумма контурных токов, протекающих по рассматриваемой ветви:
I1 = –I22 = 1,67 А; I2 = I22 + I11 = 3,33 А;
I3 = –I22= 1,67 А; I4 = I33 –I22 = 6.67 А.
Ответ: Е = 6,67 В; I1 = 1,67 А; I2 = 3,33 А;
I3 = 1,67 А; I4 = 6,67 А.
Сравнив решение задачи по методу контурных токов с решением, полученным на основании законов Кирхгофа, можно сделать вывод о том, что решение задачи с помощью метода контурных токов более рационально (менее трудоемко, так как требует меньшего числа уравнений).
Задача 4
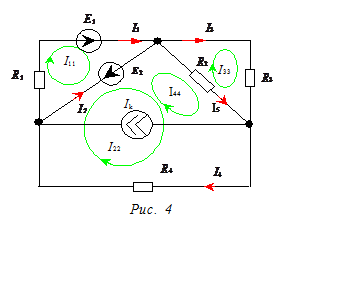 Для
выбранных, как показано на рис. 4, контурных
токов I11, I22 , I33 , I44
дать решение в общем виде для тока I1, не
прибегая к составлению системы расчетных уравнений по методу контурных токов.
Для
выбранных, как показано на рис. 4, контурных
токов I11, I22 , I33 , I44
дать решение в общем виде для тока I1, не
прибегая к составлению системы расчетных уравнений по методу контурных токов.
Решение
Значения тока I1 получим посредством составления главного определителя системы D и его алгебраического дополнения D11 (при этом необходимо учесть, что I44 = I5):
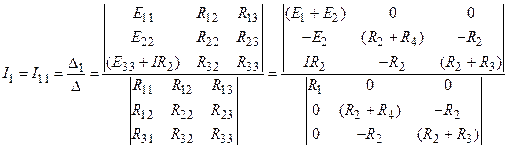 .
.
Задачи для самостоятельного решения
 |
Задача 5
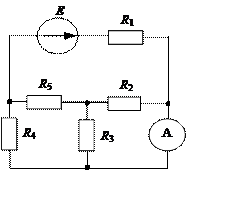
В цепи (рис. 5)
Е = 16 В; R1 = 2 Ом;
R2 = 6 Ом; R3 = 14 Ом;
R4=15 Ом; R5=5,8 Ом.
Внутренним сопротивлением
источника и сопротивлением
амперметра можно пренебречь.
Найти показания амперметра.
Ответ: I = 1,16 А.
|
Задача 6
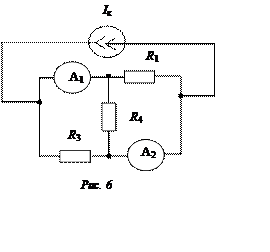 Ток, создаваемый генератором тока в цепи (рис. 6), Iк
= 60 мА.
Ток, создаваемый генератором тока в цепи (рис. 6), Iк
= 60 мА.
R1 = 800 Ом; R3 = 600 Ом;
R4 = 300 Ом.
Найти показания амперметров. Сопротивлениями амперметров и внутренним сопротивлением генератора пренебречь.
Ответ: I1 = 44 мА;
I2 = 48 мА.
Задача 7
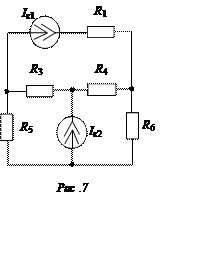 Электрическая цепь питается двумя
генераторами тока величиной
Электрическая цепь питается двумя
генераторами тока величиной
Iк1 = 20 мА,; Iк2 = 10 мА;
R1 = 5 кОм; R3 = 4 кОм;
R4 = 6 кОм; R5 = 2 кОм;
R6 = 4 кОм.
Определить напряжение на зажимах каждого из генераторов.
Ответ: Uk1 = 177,5 В,
Uk2 = 42,5 В.
III. МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ
2. Число уравнений, необходимых для расчета цепи по МУП.
3. Какой узел следует заземлить, чтобы уравнения имели наиболее простой вид?
4. Как составляются уравнения по МУП?
5. С каким знаком учитываются источники ЭДС и источники тока в правой части уравнений по МУП?
6. Какой потенциал следует принять за 0, если схема содержит одну ветвь с идеальной ЭДС. Порядок действий, если цепь содержит несколько ветвей с идеальными ЭДС.
7. Как определить токи в ветвях с идеальными ЭДС?
1. Зевеке Г.В., Ионкин П.А., Нетушил Л.В., Страхов С.В. Основы теории цепей. – М., 1989. – § 1.8, 1.3.
2. Нейман Л.Р., Демирчан К.С. Теоретические основы электротехники. – М., 1966. – Ч. 2. § 5-12.
 Задача
1
Задача
1
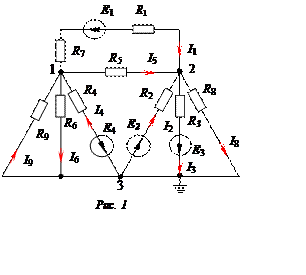
В цепи, представленной на рис. 1:
E1 = 30 B; E2 = 20 B;
E3 = 200 B; E4 = 56 B;
R1 = 20 Ом; R2 = 60 Ом;
R3 = 6 Ом; R4 = 8 Ом;
R5 = 15 Ом; R6 = 80 Ом;
R7 = 10 Ом; R8 = 60 Ом;
R9 = 80 Ом.
Определить все токи.
1. Принимаем потенциал узла 3 равным 0
![]()
2. Расчетные уравнения для определения потенциалов j1 и j2:
![]()
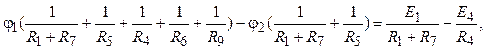 ,
,
![]()
![]() .
.
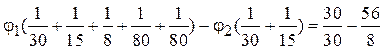 ,
,
![]() .
.
Из решения системы уравнений следует
φ1 = -80 В, φ2 = -140 B.
3. Определение токов.
Задаем произвольное направление токов во всех ветвях схемы. По закону Ома получаем:
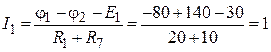 А;
А;
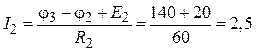 А;
А;
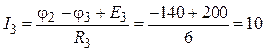 А;
А;
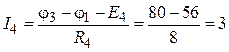 А;
А;
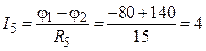 А;
А;
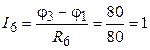 А;
А;
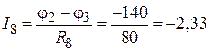 А;
А;
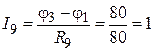 А.
А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.