IR2 –Uаb = Е2,
V= Uаb= IR2 – Е2 = 25 – 10 = 15 B.
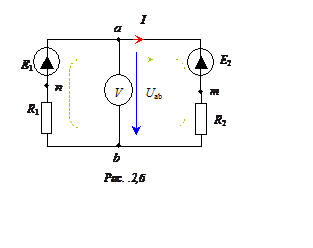
Показания вольтметра
можно также определить из уравнения, составленного по второму закону Кирхгофа
для контура
n-a-b-n (при обходе контура в направлении
движения часовой стрелки)
IR1 +Uаb = Е1,
V= Uаb = Е1 – IR1 = 40-25 = 15 В.
Ответ: Uv = 15 В.
 4.
После смены полярности одного из источников (например, Е2) на
противоположную, электрическая цепь при-мет вид, представленный на рис. 2,б.
4.
После смены полярности одного из источников (например, Е2) на
противоположную, электрическая цепь при-мет вид, представленный на рис. 2,б.
Ток в цепи определится аналогично первому случаю из уравнения по второму закону Кирхгофа (рис. 2,б)
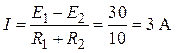 .
.
Показания вольтметра найдем с помощью уравнения по второму закону Кирхгофа для контура a-m-b-а (обход контура в направлении движения часовой стрелки)
IR2 –Uаb = –Е2,
откуда
V = Uаb = Е2+ IR2 = 10 + 25 = 25 B.
Ответ: Uv = 25 В
Таким образом, после смены полярности одного из источников показание вольтметра изменилось с 15 до 25 В.
Из данных результатов вытекает способ соединения источников при их параллельной работе.
Задача 3
В электрической цепи (рис. 3,а)
R1 = 12 Ом, R2 = 30 Ом, R3 = 20 Ом.
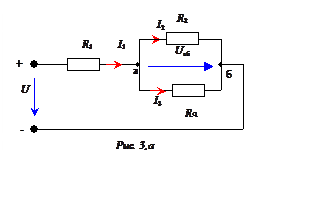 Напряжение источника питания U = 120 В. Определить токи во всех ветвях электрической
цепи и мощность, потребляемую цепью.
Напряжение источника питания U = 120 В. Определить токи во всех ветвях электрической
цепи и мощность, потребляемую цепью.
1. Эквивалентное со-противление цепи (сопротивления R2 и R3 соединены параллельно, а R1 – последовательно)
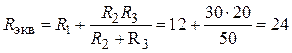 Ом.
Ом.
2. Ток I1 (на основании закона Ома)
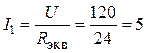 А.
А.
3. Определение токов I2 и I3:
напряжение между точками а и b (рис. 3,б)
Uаb = IR23 ,
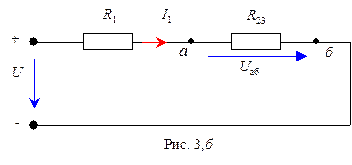
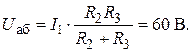
Токи в ветвях 2 и 3 (рис. 3,а)
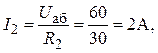
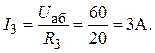
Примечание. Вышеприведенные формулы позволяют получить соотношения для более простого алгоритма определения токов в ветвях:
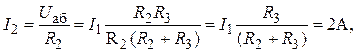
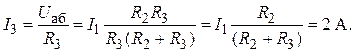
4. Мощность, потребляемая электрической цепью,
Рпотр.= S I2R = I12 R1+ I22 R2 + I32 R3 =
= 25×12 + 4×30 +9×20= 600 Вт.
Ответ: I1 = 5А; I2 = 2А; I3 = 3 А; Рпотр= 600 Вт.
Задача 4
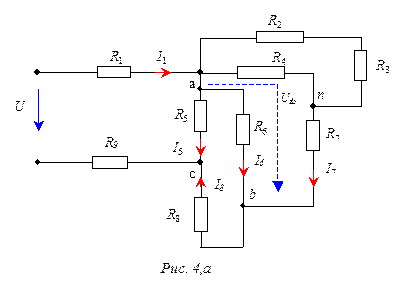
В электрической цепи (рис. 4,а):
R1 = R7 = R9 = 1 Ом,
R2 = R3 = 3 Ом,
R4 = R8 = 6 Ом,
R5 = 8 Ом, R6 = 4 Ом,
I6 = 9,16 А.
Определить напряжение U на входе электрической цепи.
Решение
1. Эквивалентное сопротивление участка a-n-b электрической цепи
R2347 = R7 +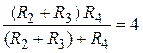 Ом.
Ом.
2. Напряжение между точками а и б (рис. 4,а)
Uab = I6 R6 = 9,16 R6 = 36,64 B.
3. Ток I7 участка цепи a-n-b
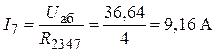 .
.
4. Ток в ветви с сопротивлением R8 (на основании первого закона Кирхгофа для узла «b»)
I8 = I6 + I7 = 9,16+9,16 = 19,32 А.
5. Напряжение между точками а и с (на основании второго закона Кирхгофа для контура a-b-c при направлении обхода контура по часовой стрелке)
Uac = Uab + Ubc = Uab+I8 R8 = 146,56 B.
6. Ток в ветви с сопротивлением R5
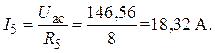
7. Ток в неразветвленной части электрической цепи (из уравнения по первому закону Кирхгофа)
I1 = I9 = I5 +I8 = 18,32 + 18,32 = 36,64 A.
8. Входное напряжение (из уравнения по второму закону Кирхгофа для контура с сопротивлениями R1 – R5 –R9 при направлении обхода контура по часовой стрелке)
-U + I1 R1+I5 R5+I9 R9 = 0,
или
U = I1×R1+Uac+I9 R9 = 146,56+2×36,64 » 220 B.
Ответ: U = 220 В.
В данной задаче возможен второй вариант решения, основанный на последовательно-параллельной свертке резистивных элементов цепи. Учитывая, что токи в параллельных ветвях с одинаковыми сопротивлениями равны и что эквивалентное сопротивление двух равных параллельно соединенных сопротивлений равно половине каждого из них, получим (величины сопротивлений указаны на схеме рис. 4,б)
U = 4I6 (1+1+4) = 4×9,16×6 = 220 B.
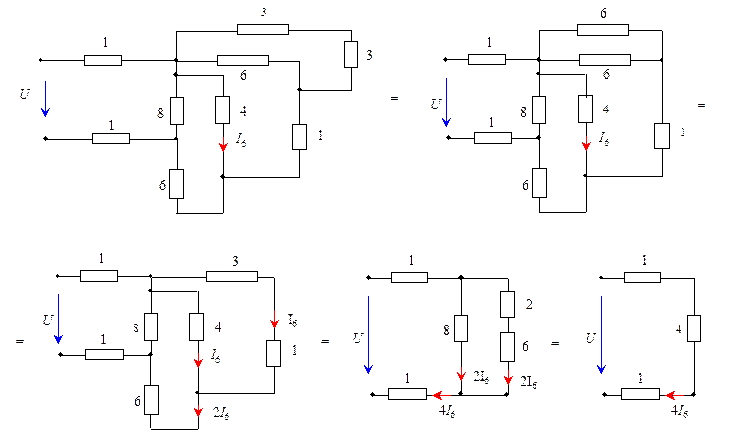
Рис. 4,6
Задачи для самостоятельного решения
Задача 5
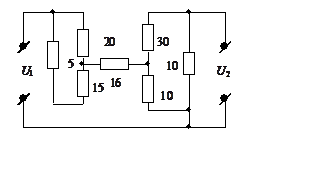
Определить отношение напряжения на выходе U2 к напряжению на входе цепи U1.
Сопротивления отдельных ветвей указаны на схеме.
Задача 6
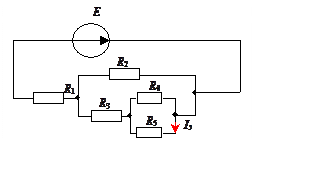 Дано:
Дано:
R1 = 0,5 Ом;
R2 = 1,4 Ом;
R3 = 3 Ом;
R4 = 2,5 Ом;
R5 = 50 Ом;
I5 = 0,2А.
Определить:
1. ЭДС источника энергии.
2. Мощность приемников энергии.
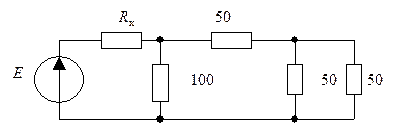
В электрической цепи все
сопротивления даны в
Омах.
Е = 200 В. Мощность, расходуемая во всей цепи, Р = 400 Вт. Определить
сопротивление Rx.
Когда два гальванических
элемента с ЭДС Е1 = 1 В и Е2 =
= 1,2 В соединили параллельно, ЭДС батареи
оказалась Е = 1,08 В, когда же к батарее подключили реостат и установили
ток
нагрузки I = 0,3 А, напряжение батареи упало до значения U
=
= 0,9 В. Определить внутреннее сопротивление батареи.
Задача 9
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.