Практический курс теоретических основ электротехники: Методическое руководство (Разделы I-VI: Основные законы электрических цепей. Электрические цепи синусоидального тока), страница 3

Лампочка накаливания, сопротивление которой R₁ = 158 Ом, питается от электрической сети  с помощью двухпроводной линии из медного провода , сечением S = 1,5 мм². Определить, на сколько процентов упадет напряжение на лампочке, если параллельно ей включить нагревательный прибор с сопротивлением R₂ = 32 Ом. Сопротивление лампочки для простоты считать постоянным. Удельное сопротивление меди r = 0,0185 Ом мм²/м.

Задача 10

Приложенное напряжение  U = 50 В.

Сопротивления заданы в Омах. Определить все токи, составить баланс мощности.

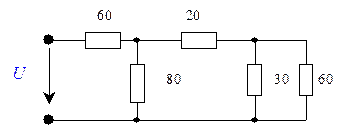
II. Непосредственное применение законов

Кирхгофа для решения задач.

Метод контурных токов

Основные вопросы

1. Количество взаимно независимых уравнений, необходимых для расчета всех токов в электрической цепи.

2. Количество уравнений, составленных на основании первого закона Кирхгофа.

3. Количество уравнений, составленных на основании второго закона Кирхгофа.

4. Общие принципы составления уравнений по методу контурных токов.

5. Порядок выбора независимых контуров. Особенности выбора независимых контуров при наличии источников тока.

6. Определение реальных токов в ветвях электрической цепи.

Литература

Зевеке Г.В., Ионкин П.А., Нетушил Л.В., Страхов С.В. Основы теории цепей. – М., 1989. §  1.5, 1.9.

ПРИМЕРЫ

Задача 1

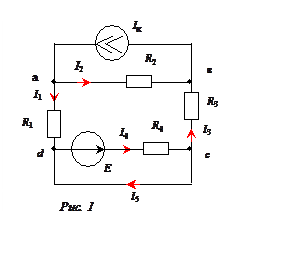В электрической цепи (рис. 1) все сопротивления одинаковы и равны 1 Ом. Ток источника тока I_к  = 5 А. Ток  в ветви с нулевым сопротивлением
I₅ = 5 А.

Определить величину и направление ЭДС. Задачу решить, используя законы Кирхгофа.

Решение

Выберем положительные направления токов в ветвях электрической цепи и направление ЭДС так, как показано на рис. 1.

Система уравнений, составленных по законам Кирхгофа:

а) по первому закону Кирхгофа (для трех произвольных узлов схемы):

I – I₁ – I₂ = 0  – для узла «а»;

–I + I₂ + I₃ = 0 – для узла «b»;

–I₅ + I₄ – I₃ = 0  – для узла «c».

в) по второму закону Кирхгофа (для двух независимых
контуров):

I₁ R₁+ I₄  R₄ + I₃  R₃ – I₂  R₂ = E, – для контура a-d-c-b-a,

I₄  R₄ = Е – для контура d-c-d.

В результате решения системы уравнений имеем:

I₂ = 5 – I₁;

I₃= 5 – I₂= 5 – 5 + I₁,   т. е.  I₃  = I_1;

I₄ = 5 + I₁;

I₁×1+ E + I₁ ×1–5 +I₁ ×1 = E,

откуда

I₁=  = 1,67 A,

I₄ = 5 + = 6,67 А,   I₂  = 3,33 А,  Е = 6,67 В.

Проверка

Проверим решение, составив уравнение баланса мощностей,

ЕI₄+ I_К (I₂ R₂) = ,

6,67×6,67 + 5×(3,33×1) = 2×1,67²×1 +3,33²×1 + 6,67²×1,

61,14 = 61,14.

Баланс мощностей выполняется, следовательно, задача решение верно.

Ответ:  I₁ = I₃ = 1,67 A,   I₂ = 3,33 A,

              I₄ = 6,67 A,  E = 6,67 B (направление ЭДС выбрано правильно).

Задача 2

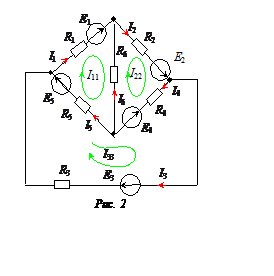
В схеме (рис. 2)

Е₁ = 18 В,  Е₂ = 5 В;

Е₃ = 5 В, Е₄  = 15 В;

Е₅ = 3 В;

R₁ = 1 Ом, R₂ = 2 Ом;

R₃ = 1 Ом, R₄ = 1 Ом;

R₅ = 1 ОМ, R₆ = 1 Ом.

Рассчитать токи в ветвях методом контурных токов.

Решение

1. Произвольно выбираем направление контурных токов в независимых контурах цепи  (рис. 2).

2. Составляем систему уравнений по методу контурных токов (направление обхода контуров принимается совпадающим с направлением контурных токов):

I₁₁ (R₁+ R₅+ R₆) – I₂₂ R₆  – I₃₃ R₅  = E₁+ E_5;

–I₁₁ R₆  + I₂₂ (R₂+R₄+R₆) – I₃₃ R₄  = E₂ – E₄;

–I₁₁ R₅– I₂₂ R₄ + I₃₃ (R₃+R₄ +R₅) = E₃ + E₄ – E₅.

3. После подстановки числовых значений имеем

 

I₁₁× 7 – I₂₂× 5 + I₃₃×1 = 21;

–I₁₁× 5  + I₂₂ ×8 – I₃₃×1 = -10;

–I₁₁×1 –I₂₂×1 + I₃₃× 3 = 17.

4. Определение контурных токов:

 

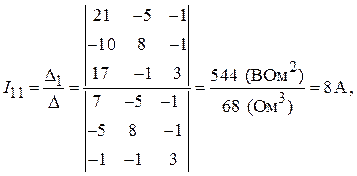
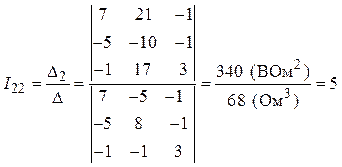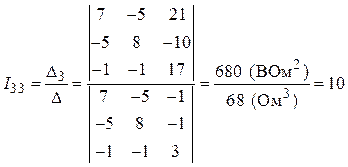 А,

 А.

5. Определение реальных токов в ветвях электрической цепи.

Реальные токи в ветвях, произвольно выбранное направление которых указано на схеме рис. 2, находятся как алгебраическая сумма контурных токов, протекающих по рассматриваемой ветви. При этом, контурные токи, совпадающие с выбранными направлениями реальных токов, учитываются со знаком «плюс», не совпадающие – со знаком «минус».

I₁ = I₁₁ = 8 А;  I₂ = I₂₂ = 5 А;  I₃ = I₃₃ = 10 А;

I₄  = I₃₃ – I₂₂ = 5 А;  I₅  = –I₃₃  + I₁₁ = –2 А;  I₆ = I₁₁ – I₂₂ = 3 А.

Ответ: I₁ = 8 A; I₂ = 5 A; I₃ = 10 A;  I₄ = 5 A;  I₅ = -2 A;  I₆ = 3 A. 

Задача 3

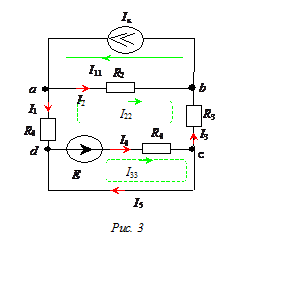По условию задачи I определить токи и ЭДС Е, пользуясь методом контурных токов.

Решение