Лабораторная работа №1э
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ТОКА НА ЭЛЕКТРОПРОВОДНОЙ БУМАГЕ МЕТОДОМ ЗОНДОВ
Краткая теория
Электростатическим полем в веществе называется поле, порождённое неподвижными электрическими зарядами и энергия которого не подвержена превращениям. Поэтому структура электростатического поля зависит от величины и распределения электрических зарядов в пространстве (среде).
Электростатическое поле характеризуется в каждой точке пространства значением вектора напряжённости поля Е и значением потенциала U . Для наглядного изображения направления вектора напряжённости поля в каждой точке пространства и распределения потенциала пользуются понятиями о силовых линиях и о поверхностях равного потенциала, называемых эквипотенциальными поверхностями.
Силовой линией или линией напряжённости электростатического поля называется такая линия, в каждой точке которой касательная совпадает по направлению с вектором напряжённости поля в этой точке пространства.
Поверхность равного потенциала или эквипотенциальная поверхность есть геометрическое место точек поля с одинаковыми значениями потенциала.
 Рассмотрим электрическое поле, создаваемое положительным
точечным зарядом q, находящимся в однородной сред». В этом случае силовые
линии представляют собой прямые (радиус-векторы), исходящие из точки, в
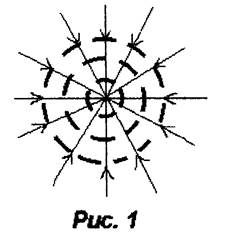
которую помещён заряд положительный q. На рис. 1 представлено
сечение картины поля точечного отрицательного заряда плоскостью чертеже.
Рассмотрим электрическое поле, создаваемое положительным
точечным зарядом q, находящимся в однородной сред». В этом случае силовые
линии представляют собой прямые (радиус-векторы), исходящие из точки, в
которую помещён заряд положительный q. На рис. 1 представлено
сечение картины поля точечного отрицательного заряда плоскостью чертеже.
Сплошные прямые - силовые линии, пунктирные окружности - следы пересечения эквипотенциальных поверхностей с плоскостью чертежа.
Силовые линии всегда совпадают по направлению с нормалями к эквипотенциальным поверхностям. Эта связь между силовыми линиями и эквипотенциальными поверхностями, показанная нами для частного случая поля точечного заряда, имеет место и в случае произвольного электростатического поля.
Действительно, рассмотрим работу перемещения точечного электрического заряда q на малое расстояние l, вдоль какой-либо эквипотенциальной поверхности. Работа А перемещения заряда на данном пути будет равна:
![]() (1)
(1)
С другой стороны, эта же работа может быть выражена как произведение величины заряда q на разность потенциалов в начальном и конечном положениях заряда:
A = q×DU. (2)
Но так как перемещение происходит вдоль эквипотенциальной поверхности, очевидно, DU = 0. Таким образом, мы получаем:
![]()
Ввиду того, что ни заряд q, ни напряжённость поля Е, ни перемещение l не равны нулю, очевидно, равен нулю косинус угла между направлением напряжённости поля Е и перемещениемl . Отсюда следует, что направление вектора напряжённости электростатического поля E нормально к эквипотенциальным поверхностям в каждой данной точке поля.
Однако вектор напряжённости поля Е и вектор нормали к эквипотенциальным поверхностям, совпадающие по направлению, противоположны по знаку: нормаль считается положительной в сторону возрастания потенциала, а вектор Е направлен в сторону действия поля на положительный заряд, то есть в сторону убывания потенциала.
Найдём соотношение между величиной напряжённости поля Еи потенциалом U поля в данной точке. Для этого будем перемещать точечный электрический заряд q в произвольном электростатическом поле из точки О с потенциалом j в точку O’ с потенциалом j + Dj (см. рис. 2).
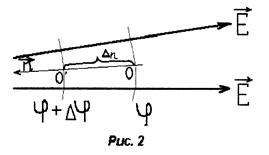 Пусть расстояние между этими точками
столь мало, что значение напряженности поля E между
ними можно считать неизменным. Проведём эквипотенциальные поверхности j и j + Dj и
восстановим нормаль к эквипотенциальной поверхности в точке O.
Очевидно, работа перемещения заряда q из точки О в точку О’
равна:
Пусть расстояние между этими точками
столь мало, что значение напряженности поля E между
ними можно считать неизменным. Проведём эквипотенциальные поверхности j и j + Dj и
восстановим нормаль к эквипотенциальной поверхности в точке O.
Очевидно, работа перемещения заряда q из точки О в точку О’
равна:
![]()
С другой стороны, эта же работа может быть выражена через разность потенциалов точек O и О’ как
![]()
Приравнивая два выражения для работы А, найдём:
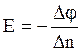
или напряженность электростатического поля численно
равна изменению потенциала на единицу длины нормали к эквипотенциальной поверхности,
взятому с обратным знаком. Величина ![]() характеризует
быстроту возрастания потенциала в направлении, перпендикуляр
характеризует
быстроту возрастания потенциала в направлении, перпендикуляр
ном эквипотенциальной поверхности, и называется градиентом потенциала. Однозначная связь между Е и j и ортогональность силовых линий и эквипотенциальных поверхностей позволяют легко перейти от изображения поля с помощью эквипотенциальных поверхностей к его изображению с помощью силовых линий и наоборот.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Постановка задачи
Целью работы является изучение различных электростатических полей, моделируемых с помощью стационарных электрических полей тока в электропроводной бумаге.
В качестве электродов предлагается использовать любые комбинации имеющихся электродов:
1. Две плоские параллельные пластины.
2. Два коаксиальных кольца.
3. Два точечных электрода.
4. Кольцо и плоский электрод.
5. Полуэллипс и плоский электрод и т.д.
Теория измерений
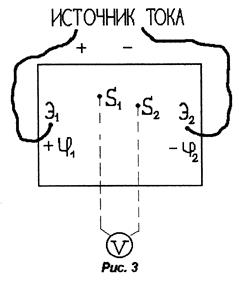 В основу изучения распределения
потенциалов в электростатическом поле часто кладётся так называемый метод
зондов. Его сущность заключается в следующем: в исследуемую точку поля вводится
специальный дополнительный электрод-зонд, по возможности так устроенный, чтобы
он минимально нарушал своим присутствием исследуемое поле. Этот зонд
соединяется проводником с прибором, измеряющий приобретенный зондом в поле
потенциал по отношению к какой-нибудь избранной за начало отсчёта точке поля.
В основу изучения распределения
потенциалов в электростатическом поле часто кладётся так называемый метод
зондов. Его сущность заключается в следующем: в исследуемую точку поля вводится
специальный дополнительный электрод-зонд, по возможности так устроенный, чтобы
он минимально нарушал своим присутствием исследуемое поле. Этот зонд
соединяется проводником с прибором, измеряющий приобретенный зондом в поле
потенциал по отношению к какой-нибудь избранной за начало отсчёта точке поля.
Но изучение электростатического поля зарядов, например, при помощи зондов, затруднено, поэтому в условиях задачи изучение электростатического поля между системой заряженных проводников можно заменить изучением его менее точней, но более удобной моделью - электростатического поля постоянного тока между той же системой проводников, если потенциалы проводников поддерживаются постоянными, а проводимость среды, в которой исследуется распределение потенциалов, намного меньше, чем проводимость данных проводников. Плохо проводящей средой может быть обыкновенная вода, влажный песок, электропроводная бумага и т.п.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.