Определение вязкости жидкости методом истечения через капилляр: Методические указания к лабораторной работе № 5фкс

Сибирский государственный индустриальный университет

Технологический факультет

Кафедра физики

ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ  ЖИДКОСТИ МЕТОДОМ

ИСТЕЧЕНИЯ ЧЕРЕЗ КАПИЛЛЯР

(Методические указания к лабораторной работе №5 фкс)

Новокузнецк

2002

КРАТКАЯ ТЕОРИЯ

Цель лабораторной работы- уяснить теорию течения жидкости через капилляр и измерить вязкость воды.

Описание явления.  При движении потока в трубах и каналах по сечению трубы устанавливается неравномерное по сечению распределение скоростей. Вблизи твердой поверхности частицы жидкости заторможены. Для частиц жидкости на внутренней поверхности трубы скорость  равна нулю. Вследствие сцепления между ними и твердой поверхностью,  они как бы «прилипают» к последней. При удалении от поверхности  скорость возрастает. Влияние вязкости проявляется в торможении частиц в разных слоях. При этом максимальное значение скорости будет на оси трубы. Характер распределен скорости в рассматриваемой точке и, соответственно, профиль скорости потока в поперечном сечении трубы зависит от режима течения потока (ламинарный или турбулентный). Ламинарное движение имеет слоистый характер и происходит без перемешивания частиц. Каждый слой движется по-другому, причём между ними возникает сила, тормозящая быстрые слои и ускоряющая медленные, и приводящая к появлению касательных напряжений:

              

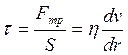
касательное напряжение, v-скорость жидкой частицы вдоль оси трубы, r-координата её,  - градиент скорости (см. рис.2), S-площадь поверхности, разделяющей слои, -коэффициент динамической вязкости, характеризующий сопротивление смещению слоёв.

Этот закон был установлен И. Ньютоном (1687г.). Существуют очень вязкие жидкости, например, глицерин, для которого =4,2¸0,7 Па×с в диапазоне температур от 3°С до 20°С. Обычные жидкости (вода, спирт, жидкие металлы) имеют вязкость порядка 10^-3Па×с.

Вывод расчетной формулы. Рассмотрим стационарный поток жидкости, ламинарно текущей через капилляр круглого сечения (рис.1). Мысленно выделим в жидкости цилиндр радиуса  и длины l. Обозначим давление на его торцах через Р₁ и P₂. В стационарных условиях сила давления на цилиндр  (P₁ - P₂)pr² уравновешивается силой трения, действующей на цилиндр со стороны наружных слоев жидкости. Эта сила равна F_тр = Sh(dv/dr). Заменяя S через 2лr1 и из условия равновесия приравнивая нулю сумму сил, действующих на цилиндр, получим:

       

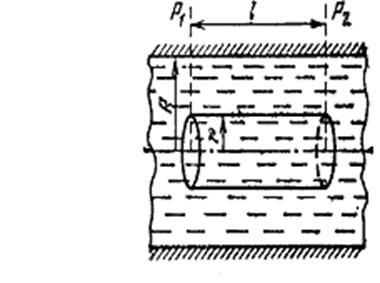
Рис.1 – Стационарный поток жидкости, ламинарно текущий через капилляр.

(P₁ - P₂)pr² + 2prlh(dv/dr) = 0

Интегрируя это равенство, найдем

            ,

где С—константа интегрирования, которая должна быть найдена из граничных условий. Чтобы найти ее, заметим, что скорость жидкости обращается в нуль на границе трубкипри радиусе r=R, где жидкость «прилипает» к стенкам. Следовательно:

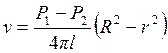                                                                     (1)

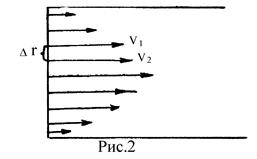
Таким образом, скорость жидкости квадратично меняется c радиусом и максимальна на оси трубки (при  = 0). Эпюрой скорости (кривой, огибающей концы векторов скоростей) является пароболоид вращения (рис.2), осевое сечение называется параболой Пуазейля по имени французского врача, исследовавшего закомерности движения крови по капилярным сосудам (1840 г.).

                   

  Расход жидкости Q, т. е. объем, ежесекундно протекающий через поперечное сечение трубки, равен

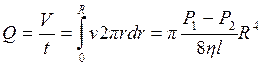                                            (2)       

Формула (2) носит название формулы Пуазейля. Из этой формулы следует, что вязкость жидкости можно определить, измеряя ее расход Q, перепад давления (Р₁ - Р₂), длину трубки l и ее радиус R. Наиболее простую формулу для экспериментального определения вязкости получим из соотношения  для объёма жидкости V, вытекшей из трубки за время t: V=Q×t, тогда, с учетом (2) находим коэффициент вязкости жидкости:

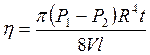                                                         (3)

Единственной неопределенной величиной в (3) является разность давлений. Для определения его используют различные измерительные устройства. В нашем случае выбран наиболее простой и надежный способ основанный на измерении  высоты жидкости в входном сосуде.

Описание эксперимента. Прибор для определения h состоит из стеклянного сосуда А, наполненного испытуемой жидкостью (рис. 3). К нему присоединена капиллярная трубка СД. Исследуемая жидкость стекает в сосуд Е. Подставка F служит для поднятия и опускания трубки.

В начальный момент вытекание жидкости происходит под давлением столба жидкости высотой h’—h, в конце опыта под давлением столба жидкости высотой h’’- h. Усредняя, получим высоту столба жидкости, под давлением  которого жидкость протекает за время t через капилляр:

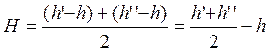                                         (4)

Величина давления столба жидкости высотой Н определяется по формуле:

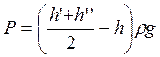                                                                  (5)

где r — плотность жидкости, g — ускорение свободного падения. Тогда Р₁- Р₂ = Р₀ + Р- Р₀= Р, здесь Р₀-атмосферное давление.

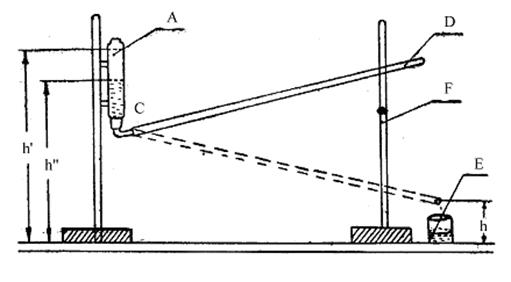Рис.3. Прибор для определения коэффициента внутреннего трения.

Объём жидкости определяется по делениям мерной мензурки. Длина и радиус капиллярной трубки записаны на штативе прибора или должны быть выяснены у преподавателя. Время измеряется секундомером.

Порядок выполнения работы

1. Определить высоты h’, h.

2. Капилляр СД быстро опустить  с верхнего крючка на нижний. Через некоторое  время, когда в сосуде наберется 50—100 мл жидкости, трубку быстро возвратить в первоначальное положение. При этом отсчитать по секундомеру время tистечения жидкости через капилляр.

3. Измерить высоту h.

4. По формуле (5) определить давление Р, а по формуле (3)  коэффициент вязкости . 

5. Все данные занести в таблицу.

6. Перелить воду из сосуда Е в сосуд А и повторить пункты 1-5 ещё два раза.

7. Полученные три значения вязкости обработать по формуле прямых измерений с указанием среднего и доверительного интервала.

8. Сравнить полученные значения вязкости с табличными данными.

Контрольные вопросы для допуска к работе.

1.  Какова цель работы?

2.  Порядок выполнения работы.

3.  Какие измерения будут производиться?

4.  В каком виде представляются результаты измерений?

Вопросы для защиты.

1.  Явление внутреннего трения в жидкостях и газах.

2.  Что является гидростатическим давлением?

3.  Формула Пуазейля.

4.  Вывод расчетной формулы.

Список рекомендуемой литературы.

1.  Савельев И.В. Курс общей физики. Т1. - М.: Наука, 1974. - 162с.

2.  Трофимова Т.И. Курс физики. М.: Высшая школа, 1990. - 478с.

3.  Физический практикум. / Под редакцией Ивероновой В.И. М.: Наука, 1967. – 125с.

4.  Обработка наблюдений и представление результатов эксперимента. Метод. указания. / Сост.: Петрунин В.А., Громов В.Е., Березовский В.Н., Мальцев В.Д. Новокузнецк : СибГИУ, 1999. – 46с.