Дифракция Френеля. Дифракция Фраунгофера на щели (на нити, на круглом отверстии) (Лабораторная работа № 4лок)

Лабораторная работа 4 лок

ДИФРАКЦИЯ ФРЕНЕЛЯ. ДИФРАКЦИЯ ФРАУНГОФЕРА НА ЩЕЛИ (НА НИТИ, НА КРУГЛОМ ОТВЕРСТии)

Краткая теория

1. К ТЕОРИИ ДИФРАКЦИИ ФРЕНЕЛЯ — ФРАУНГОФЕРА-КИРХГОФА

Дифракция проявляется в перераспределении исходного потока энергии при распространении колебаний в среде с резкими неоднород­ностями. В результате появляется устойчивая зависимость интенсивности проходящего или отраженного излучения от направле­ния.

Формализованное количественное описание дифракции осно­вано на принципе Гюйгенса — Френеля, реализованном в наиболее общем виде Кирхгофом (кинематическая теория).

В первом приближении описание дифракции дает направления максимальной и минимальной интенсивностей, не оценивая интенсив­ностей количественно (геометрическая теория).

Более глубокое описание основывается на уравнениях Мак- ­свелла и электронной теории вещества (динамическая теория).

Пространство, в котором реализуются исследуемые колебания, называется волновым полем.

Согласно принципу Гюйгенса — Френеля, каждый элемент неко­торой волновой поверхности является самостоятельным источни­ком вторичных сферических волн, а колебание в каждой точке волно­вого поля — результат интерференции вторичных волн.

Применим принцип к свету в вакууме, используя метод зон Фре­неля (рисунок 4.1).

Пусть Ф — мгновенное положение сферического фронта моно­хроматической волны от точечного источника Р. Построим вокруг точки Р сферы с радиусами ( Я — длина волны)

Сферы делят фронт на зоны с внешними радиусами

и площа­дями номер зоны.

Амплитуда колебаний в точке Р

где - например, «световой вектор» (напряженность электри­ческого поля).

С учетом разности хода колебаний от соседних зон:

Рис. 4.1- Использование метода зон Френеля для качест­вен­ного анализа дифракции

Амплитуда волны зоны уменьшается с ростом номера зоны за счет расстояний l₁ и l₂ и угла Х между нормалью к фронту и направлением в точку интерференции Р. Предполагая

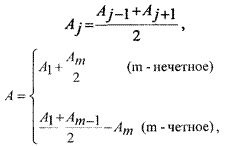имеем

если открыто т центральных зон;       если открыты все зоны; А = А₁, если открыта только первая зона;          , если открыты только четные или нечетные зоны; A=A_min, если открыто четное число зон (в центре дифракционной картины темное пятно);                  , если за­крыто m центральных зон Фре неля.

В случае ограниченного расходящегося (или сходящегося) пучка и перекрытия части центральных зон на открытом участке фронта может быть нечетное или четное число зон, светлое или тем­ное пятно в центре дифракционной картины, соответственно.

Если m>>1, то A=A_m+1/2 <<A₁»0, и за преградой наблюдается ее четкая тень (область геометрической оптики); т~1— область дифрак­ции Френеля; m<<1 — область дифракции Фраунгофера (в центре дифракционной картины светлое пятно).

При количественном описании дифракции фронт волны на пре­пятствии разбивается на элементарные участки. Амплитуда и фаза волны от каждого элемента определяется его положением относи­тельно источника и точки интерференции. Частный случай представ-лен на рисунке 4.2.

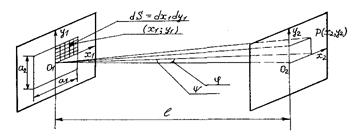
Рис.4.2 — К дифракции плоской волны на прямоугольном отверстии

Задача сводится к интегрированию по поверхности открытой части фронта для заданного направления дифракции. Решением явля­ется интерференционная функция, описывающая распределение интенсивности дифрагированной волны по направлениям в зависимости от параметров препятствия и длины волны излучения.

1.1.ДИФРАКЦИЯ В ПАРАЛЛЕЛЬНЫХ ЛУЧАХ НА ПРЯМОУГОЛЬ­НОМ И КРУГЛОМ ОТВЕРСТИЯХ

Направление дифракции, соответствующее  точке P(x,y,z) дифракцион­ной картины, задаётся углами j и ψ (рисунок 4.2).

Амплитуды от всех волн в заданном направлении дифракции оди­наковы. В результате интегрирования по открытой отверстием части волновой поверхности получается интерференционная функция

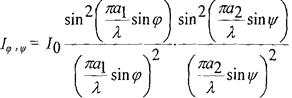(4.1)

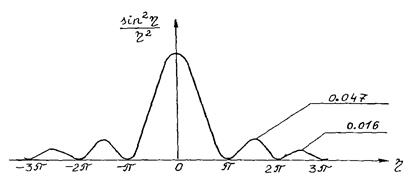
При          , интенсивность равна I₀,. Графически каждый из со­множителей представлен на рисунке 4.3.

Рис.4.3. График функции                 , представляющей сомножи­тели интерференционной функции (4.1)

Направления и координаты минимумов

(4.2)

где

Направления и координаты максимумов

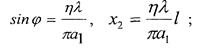
(4.3)

Дифракционные максимумы образуют дифракционную картину в виде креста.

Таким образом, с ростом размера отверстия (а) дифракционная картина в соответствующем направлении сжимается. Так, при величина дифракционного изображения отверстия по оси у становится равной размеру отверстия а₂(дифракция на щели). Для щели интерференционная функция принимает вид