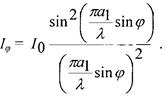Дифракция Френеля. Дифракция Фраунгофера на щели (на нити, на круглом отверстии) (Лабораторная работа № 4лок), страница 2

 

(4.4)

Для минимумов

 

(4.5)

Для максимумов

 

(4.6)

где

Случай круглого отверстия представляет большие трудности в расчетах. Общий ход распределения интенсивности в дифракционной картине подобен случаю прямоугольного отверстия, но максимумы и минимумы располагаются в фокальной плоскости линзы в виде концен­трических колец.

Дифракционная картина от круглого диска аналогична дифракци­онной картине от круглого отверстия.

1.2.ДИФРАКЦИЯ НА ОДНОМЕРНЫХ ПЕРИОДИЧЕСКИХ СТРУКТУРАХ

Если у нас есть цепочка из М отверстий вдоль оси х с периодом d=a+в  (а — размер отверстия, в — промежуток между отверстиями), то интерференционная функция имеет вид

 

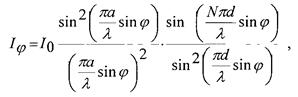(4.7)

где I₀ — интенсивность от одной щели в направлении j= 0, j - угол дифракции. Первый член представляет распределение интенсивности от каждого отверстия, второй — интерференцию N- пучков, исходя­щих от всех отверстий. Для главных максимумов

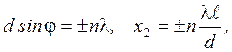                             (4.8)

где n=0,1,2...- порядок главного максимума.

Для главных минимумов

 

(4.9)

где т=1,2,3... Между соседними главными максимумами имеется      (N — 2) слабых побочных максимума и (N — 1) побочных миниму­мов. Для последних

 

(4. 10)

где ρ— целые числа, кроме N,2N,3N и т. д.

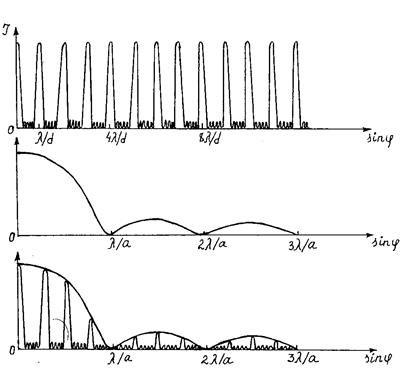
Рис.4.4. Интерференционная функция одномерной периодической структуры

На рисунке 4.4 показаны сомножители и ин­терференционная функция для случая N=6, d/a=K=4, К — кратность периодической структуры.

Угловая ширина главного максимума — расстояние между приле­гающими к нему дополнительными минимумами

 

(4.11)

При освещении решетки белым светом на экране должен наблю­даться неокрашенный центральный максимум, а по обе стороны от него — дифракционные спектры, в которых происходит непрерывный переход от сине — фиолетового цвета у внутреннего края к красному у внешнего.

2. НЕКОТОРЫЕ ОБЩИЕ ЗАКОНОМЕРНОСТИ

ДИФРАКЦИИ

ВВЕДЕНИЕ

Под дифракцией в общем случае понимают явление перераспре­деления интенсивности света при распространении волн в среде с рез­кими неоднородностями, связанное с отклонениями от законов геомет­рической оптики. Дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Согласно принципу Гюйгенса-Френеля, амплитуда колебаний волны в данной точке определяется интерференцией вторичных сферических волн от некоторой волновой поверхности.

Вследствие дифракции размер освещенной области на экране, установленном на расстоянии Lот щели будет превышать начальные размеры пучка d на дополнительное дифракционное уширение (рисунок 4.5).

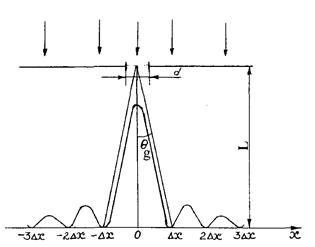
Рис. 4.5. Распределение интенсивности при дифракции

(4.12)

где h — размер изображения щели.

 

Если впагг,  ,то размер пятна практически равен d, распределе­ние интенсивности определяется законами геометрической оптики.

Расстояние      , на котором дифракционное ушире ние становится срав­нимым с начальным размером пучка             , называется длиной ди­фракции. Угловая ширина наиболее яркого центрального максимума (рисунок 4.5) находится по формуле

 

(4.13)

и является фундаментальным параметром в дифракции и позво- ­ляет оценить порядки дифракционных эффектов. Смысл этого параметра: любое пространственное ограничение волны вызывает её расхождение в соответствии с (4.13). Используем определение L_g как                                                

и получаем из (4.13)

 

(4.14)

Характер распределения интенсивности в дифракционной кар­тине зависит от безразмерного параметра дифракции

 

(4.15)

Таким образом, если

1) - область геометрической оптики,

2)  - область дифракции Френеля. Это наиболее сложная для анализа ситуация. Параметр т определяет число зон Фре­неля, на которые разбивается волновая поверхность так, чтобы вторичные волны от соседних зон приходили в противофазе. Радиус отверстия, в котором укладывается m первых зон Френеля, определя­ется как

 

(4.16)

 

3)                       - область дифракции Фраунгофера. В этом случае харак­тер распределения интенсивности на экране и расчет дифракцион­ной картины существенно упрощается. Лучи, идущие от различных участков волновой поверхности источника в произволь­ную точку экрана можно считать параллельными, а приходящую в эту точку волну — плоской. Таким образом, в дифракции Фраунгофера интерферируют вторичные волны, исходящие из волновой поверхно­сти, за­ключенной в области значительно меньше первой зоны Френеля.