Расчет регулятора для двухканальной системы полиномиальным методом синтеза

1. Постановка задачи

1.1. Цель работы

Рассчитать регулятор для двухканальной системы полиномиальным методом синтеза.

1.2. Исходные данные

     Объектом управления является система из трех масс , последовательно соединенных пружинами жесткостью . Массы, а также их координаты  пронумерованы сверху вниз. Предполагается два управляющих сигнала – силы  и , приложенные к массам  и . Управляемыми величинами являются координаты грузов  и , отсчитываемые от состояния равновесия.

Таблица 1. Исходные данные

Рис. 1. Физическая модель объекта

2. Расчёт регулятора

2.1. Математическая модель объекта

В предположении отсутствия демпфирования модель объекта «вход – выход» следующая:

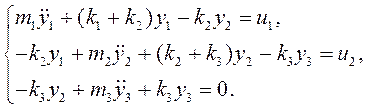
Перейдём к изображениям:

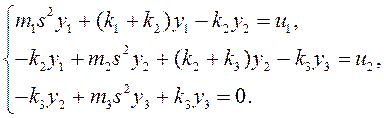
               Сгруппируем переменные:

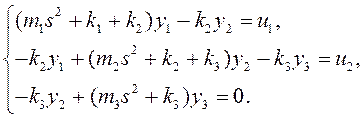                                              (1)

Перейдём к полиномиальному описанию:

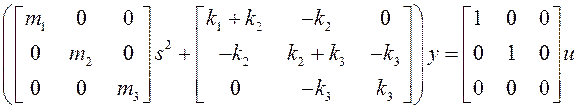
Здесь и .

С учётом исходных данных запишем:

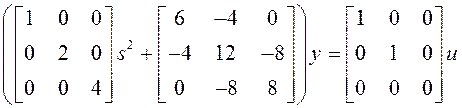
Обозначим матрицы при  и  через  и  и :

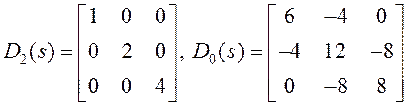
Рис. 2. Модель объекта в системе Simulink

Рис. 3. Переходные процессы y(t) в объекте

2.2. Левое полиномиальное разложение объекта

Умножив второе уравнение (1) на множитель , исключим переменную  из системы:

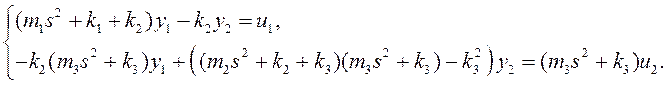
Запишем матричную передаточную функцию в полиномиальном виде:

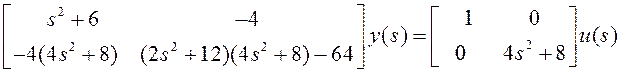
Или в матричных обозначениях

,

что соответствует левому полиномиальному разложению объекта. Здесь

.

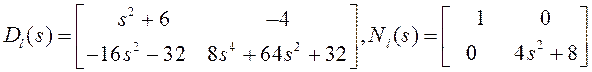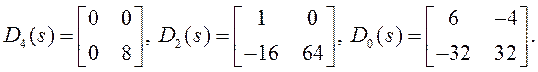
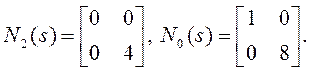
Нами найдено левое разложение матричной передаточной функции:

.

2.3. Правое полиномиальное разложение объекта

Найдём правое полиномиальное разложение объекта:

.

Для начала приведем матрицу  к верхнетреугольному виду:

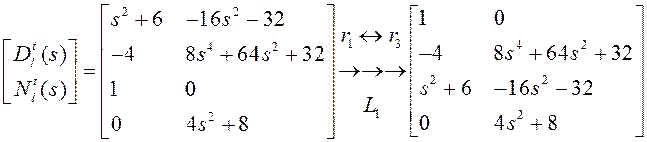
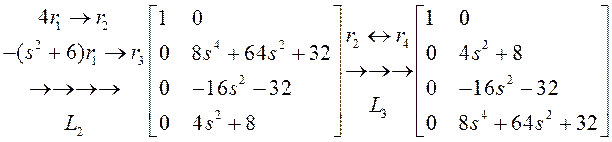
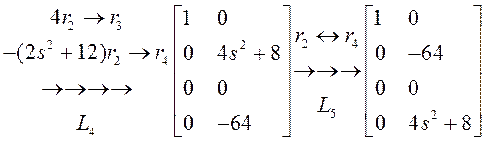
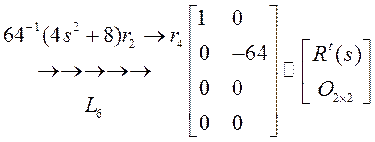
Выпишем матрицы :

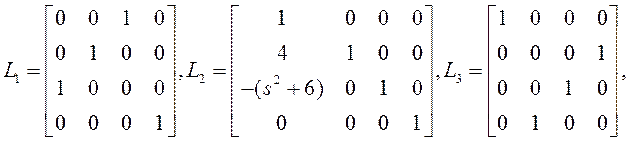
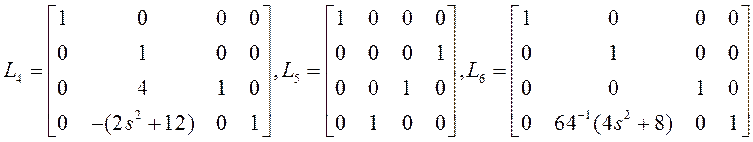
Найдем результирующее преобразование:

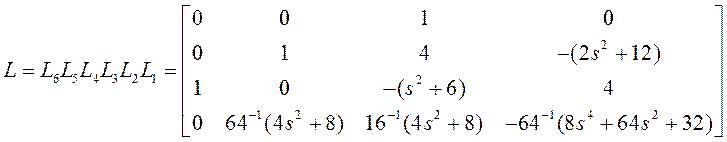
Для проверки умножим  слева на и получим тот же результат , или

.

Здесь

.

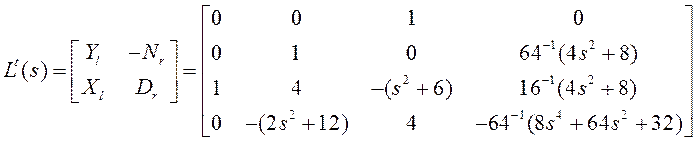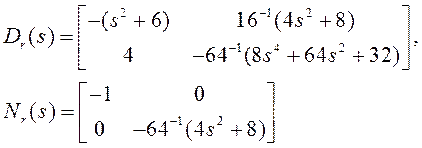
Получили правое взаимно простое разложение матричной передаточной функции объекта. Можно проверить равенство , или, что эквивалентно, равенство .

2.4. Составление диофантова уравнения

«Отнормируем» матричную передаточную функцию объекта, представленную в виде правого разложения – умножим «числитель»  и «знаменатель»  на «–64». В результате коэффициент при старшей степени  окажется равным единице:

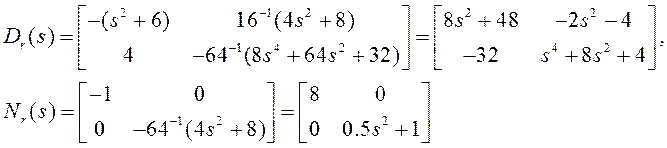
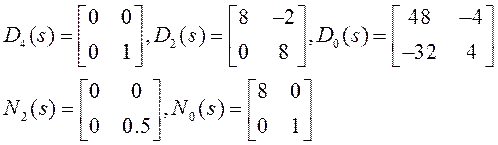
Опишем систему уравнениями

 ,

где – выход объекта, – выход регулятора, – задание.

Найдем передаточную функцию системы:

.

Задав регулятор в виде левого полиномиального разложения , получим

.

Выберем структуру «числителя» и «знаменателя», т. е. выберем порядки, например равными трем и трем:

, .

Таким образом, при известном правом представлении объекта в предположении, что ищем регулятор в виде левого разложения, задача синтеза сводится к решению диофантова уравнения:

                                                         (2)               

где – характеристическая матрица системы размером 2 на 2. Приравняв коэффициенты при одинаковых степенях s, получим систему уравнений, которая в матричном виде запишется так: . Далее следует решать диофантово уравнение, выбирая каким-либо образом степени матриц , , .

2.5. Решение диофантова уравнения

Запишем диофантово уравнение в матричном виде:

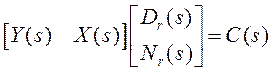
Зададим . Тогда:

,

.

Можем выписать “структуру” матриц  и :

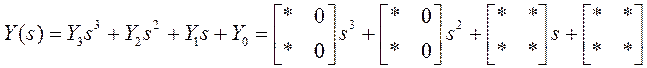
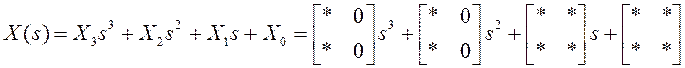
где звездочками помечены элементы, подлежащие определению.

          Подставим , , ,  в (2):

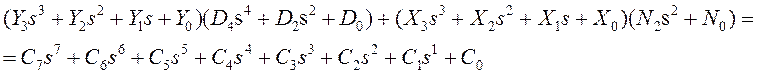
Приравняв коэффициенты при  с одинаковыми степенями в левой и правой части получим систему линейных уравнений, которую можно записать в матричном виде

.                                                         (3)

Здесь:

, ,

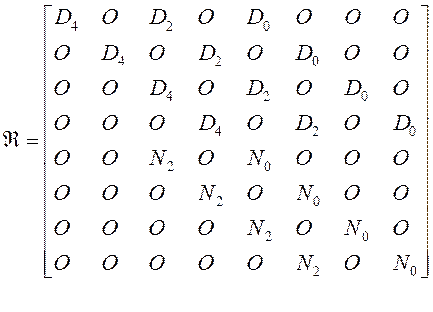                              (4)

Получили систему матричных уравнений с 8-ью матричными неизвестными и восемью матричными уравнениями. Подставим значения ,  в (4).

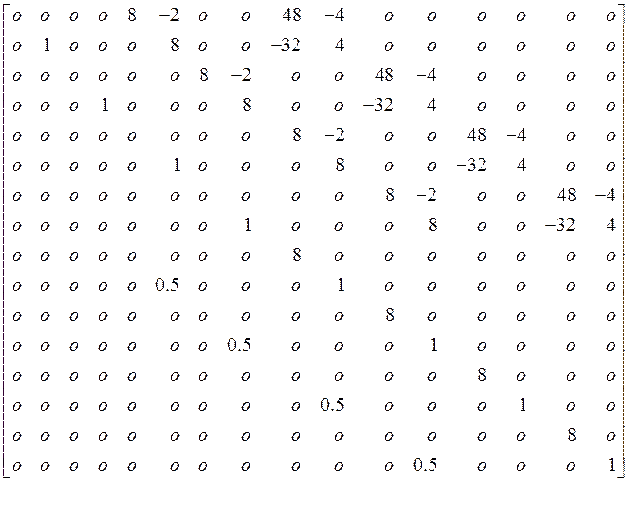
Учтем структуру регулятора, а именно, что вторые столбики матриц , , ,  - нулевые. Это соответствует нулевым значениям столбиков 2, 4, 10, 12 матрицы :

.

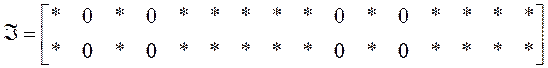При умножении  на  строки 2, 4, 10, 12 матрицы  не играют роли и их можно выбросить вместе со столбцами 2, 4, 10, 12 матриц . После этого столбцы 1, 2, 3, 4 матрицы  оказываются нулевыми. Следовательно, столбцы 1, 2, 3, 4 матрицы  обязаны быть нулевыми – это ограничение на выбор матрицы . В итоге мы обязаны выбросить из  и из  столбцы 1, 2, 3, 4. Матрицу  после выбрасывания столбцов 2, 4, 10, 12 обозначим через :