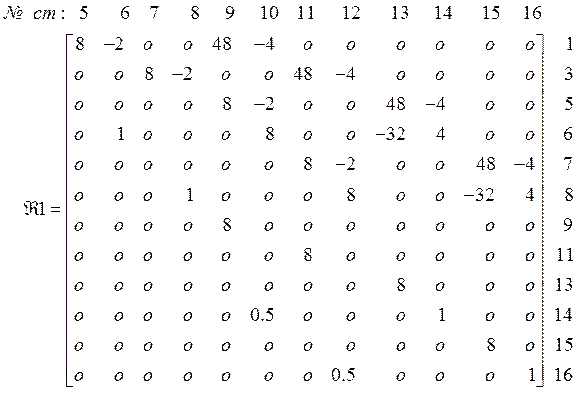Расчет регулятора для двухканальной системы полиномиальным методом синтеза, страница 2

                                   

,

 .

Матрицу  после выбрасывания строк 2, 4, 10, 12 и столбцов 1, 2, 3, 4 обозначили через . Матрицу  после выбрасывания столбцов 1, 2, 3, 4 обозначим через :

                    

.

Получили систему уравнений . Проверим матрицу  на вырожденность - . Нужно убрать две линейно зависимые строки. По очереди убираем по одной строке из матрицы : при удалении строк 5, 7, 9, 11, 13, 14, 15, 16 (в исходной нумерации) ранг не понижается. Следовательно, строки нужно убирать из этого набора. Теперь будем убирать по две строки в матрице  из набора 5, 7, 9, 11, 13, 14, 15, 16. При удалении строк 7 и 14 (нумерация строк сохранена из матрицы ) ранг остается равным 10. Следовательно, строки 7 и 14 линейно зависят от остальных строк. В уравнении  в матрице  им соответствуют столбцы 7 и 14, т.е. первый столбик  (обозначим ) и второй столбик  (обозначим ). Левую часть  можем “расщепить” на две части:

 .                                               (5)

Здесь:

                         

,

                                             

           

,

                                 

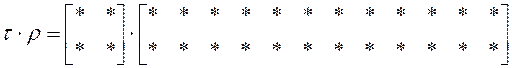
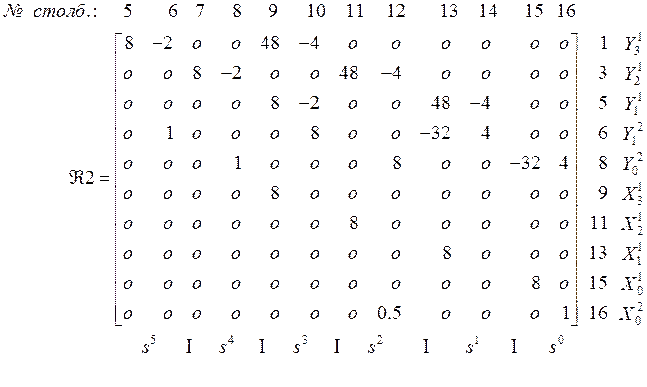
Ранг матрицы  равен 10, а столбцов 12 – найдем линейно зависимые столбцы. Это столбцы 6 и 8 в исходной нумерации. Из (5) следует, что 6 и 8 столбики в  произвольно задавать нельзя. Преобразуем (5):

.                                      (6)

Из выше сказанного следует, что из  и  исключаем столбики 6 и 8, в результате чего (6) преобразуется в уравнение

,                                                  (7)

где . Матрицы  и  получены из  и  вычеркиванием 6 и 8 столбцов:

=

  

.

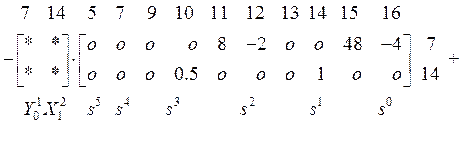
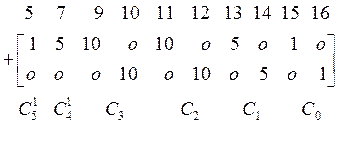Полином  задали равным . Полином  смогли задать только частично:

.

Коэффициенты при  и  произвольно задавать не можем. Для решения (6) необходимо задать матрицу  - часть параметров регулятора. Выберем  равной единичной матрице. Тогда

  

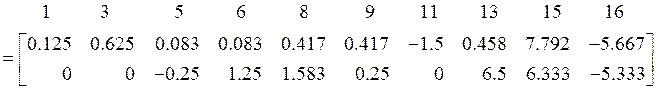
Чтобы восстановить , следует вспомнить, что столбики 2, 4, 10, 12 – нулевые, а 7 и 14 – составляют матрицу :

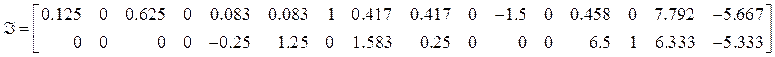
Вспомнив структуру , , : ,

, , можем выписать “числитель” и “знаменатель” регулятора:

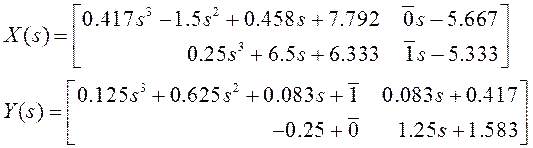                  (8)

Числа, отмеченные черточкой – это элементы матрицы , заданной произвольно – в нашем случае  приравняли к единичной матрице. Найденное решение (8) зависит от выбора . Воспользуемся (3) для вычисления :

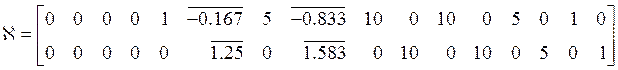
Помеченные числа произвольно задавать не можем – их значения зависят от выбора  и “внутренних зависимостей”. По матрице  можно восстановить характеристическую матрицу :

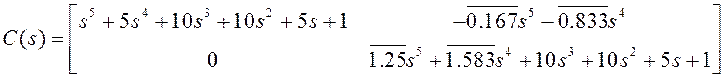
Выделенные коэффициенты произвольно задавать не можем. Таким образом, по второму каналу получили полином:

,

          характеристические числа которых равны:

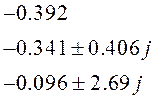
          Вещественные части характеристических чисел отрицательны, следовательно, система с регулятором устойчива.

Выводы

          В итоге для исходного объекта, который изначально находился на границе устойчивости (см. рис. 3) был рассчитан регулятор. Для первого канала смогли задать коэффициенты желаемого полинома произвольно. Для второго канала ряд коэффициентов желаемого полинома  произвольно задать не смогли. Кроме того, между каналами имеется перекрёстная связь . Но так как вещественные части характеристических чисел полиномов первого и второго каналов отрицательны, можно сделать вывод, что система с рассчитанным регулятором будет устойчива.

          Построить систему с регулятором не представилось возможным, т.к. матрица  регулятора вырожденная, а для построения модели регулятора необходимо использовать матрицу .

Приложение

Далее представлен программный код для вычисления некоторых матриц

Исходные данные

Расчёт