Ознакомление с квадратурными формулами Ньютона-Котеса численного интегрирования

Министерство образования Российской Федерации

Новосибирский государственный технический университет

Лабораторная работа №2

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Вариант №6.

Выполнили:

Якименко А. А.

Григорьев В. В.

Крылысов А. В.

Группа: АП – 419

Факультет: АВТ

Проверил:

Соловьев

Новосибирск

2006 г.

1. Цель работы

            Ознакомиться с квадратурными формулами Ньютона-Котеса численного интегрирования, исследовать влияние порядка точности квадратурной формулы и шага интегрирования на точность вычисления определенного интеграла.

2. Постановка задачи

            Вычислить определенный интеграл

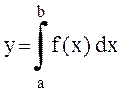,    a=0,  b=8

от функции  f(x), заданной на  [a, b]  с шагом   (= 0,1,  0,2,  0,4), посредством квадратурных формул:

            m = 0 - формула прямоугольников (левых прямоугольников);

            m = 1 - формула трапеций (Ньютона-Котеса первого порядка точности);

            m = 2 - формула парабол (Ньютона-Котеса второго порядка точности);

            m = 3 - формула "трех восьмых" (Ньютона-Котеса третьего порядка точности);

            m = 4 - формула Ньютона-Котеса четвертого порядка точности.

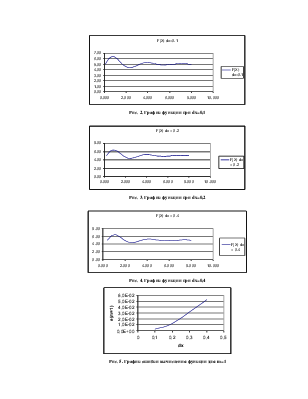
            Исследовать влияние шага дискретизации  функции f(x) на точность вычисления интеграла.

            При вычислении погрешностей интегрирования e = |yт – y| за точное значение интеграла yт следует принять его значение, вычисленное с минимальным шагом и максимальным порядком точности m квадратурной формулы.

Таблица 1.1

3. Краткие теоретические сведения

Квадратурные формулы для m = 1; 2.

Полагая m = 1, получим формулу трапеций

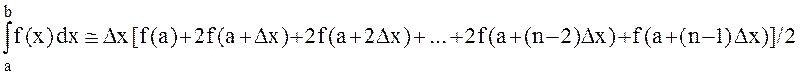При m = 2 имеем формулу парабол (n - число четное)

.

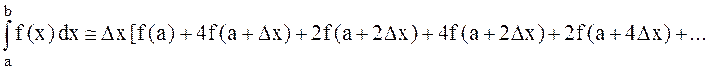
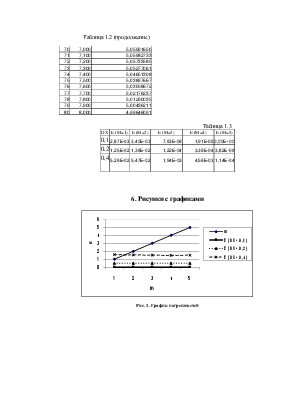
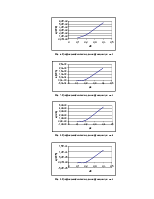
Для построения графиков функций использовалась программа GRAPH (доступна на FTP сервере НГТУ кафедры АС: ftp://ac.cs.nstu.ru/pub/hell/work/wiymet/graph/), использующая выходные данные программы, приведенной в пункте 4.

4. Листинг программы на языке FORTRAN

      real x(100),y(100),f,yt,e1(5,3),f1(5,3)

      a=0

      b=8

      dx=0.1

      do 1 j=1,3

      write(5,10)

      do 2 m=5,1,-1

      n=(b-a)/dx+1

      do 3 i=1,n+1

      x(i)=a+dx*(i-1)

      y(i)=5+2*exp(-0.5*x(i))*sin(2*x(i))

3     write (5,*) dx, m,x(i), y(i)

      call n1yink(y,n,dx,m,f)

      f1(m,j)=f

      yt=f1(5,1)

2     e1(m,j)=yt-f

1     dx=dx*2

      write(5,15)

      dx = 0.1

      do 5 i=1,5

      do 6 j=1,3

      dx=a+dx*(i-1)

      write(5,*) e1(i,j)

6     dx=dx*2

5     continue

10    format (12x,'dx',14x,'m',14x,'x',14x,'y')

15    format (10x,'dx',16x,'m', 16x,'e')

      stop

      end

5. Результаты вычислений.

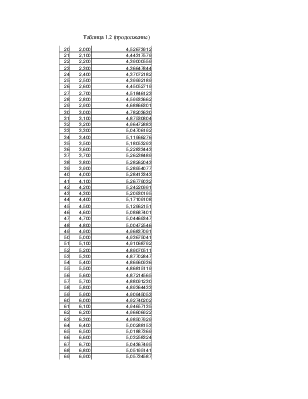
Таблица 1.2