Математика \ Вычислительная математика

Ознакомление с квадратурными формулами Ньютона-Котеса численного интегрирования, страница 3

Таблица 1.3

DX

E (M=1)

E (M=2)

E (M=3)

E (M=4)

E (M=5)

0,1

2,87E-03

3,40E-03

7,63E-06

1,91E-05

0,00E+00

0,2

1,25E-02

1,36E-02

1,22E-04

3,36E-04

3,82E-06

0,4

5,26E-02

5,47E-02

1,94E-03

4,56E-03

1,14E-04

6. Рисунки с графиками

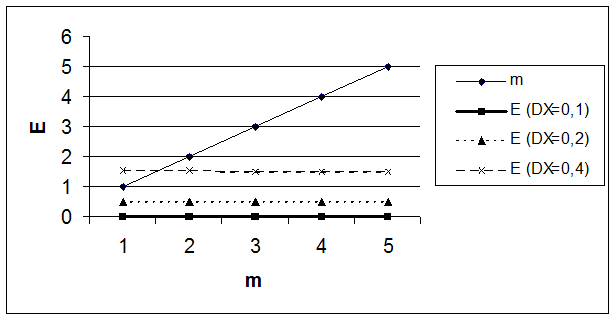
Рис. 1. График погрешностей

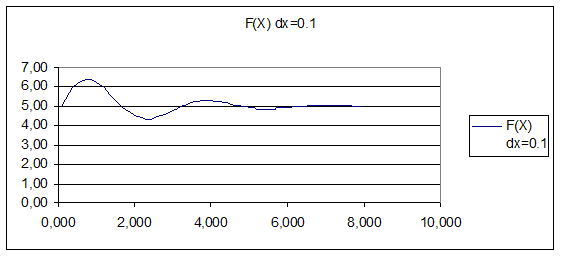
Рис. 2. График функции при dx=0,1

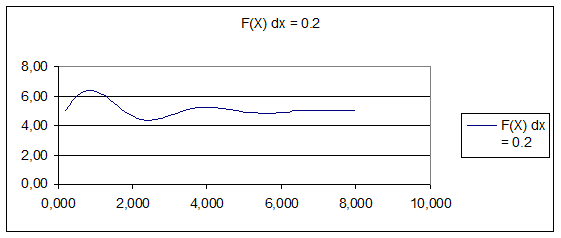
Рис. 3. График функции при dx=0,2

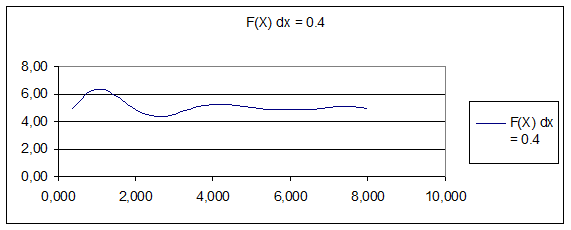
Рис. 4. График функции при dx=0,4

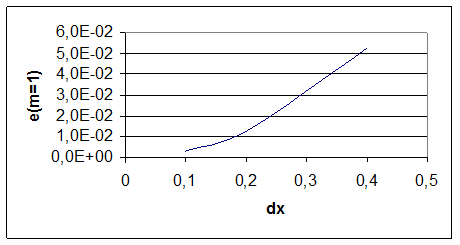
Рис. 5. График ошибки вычисления функции для m=1

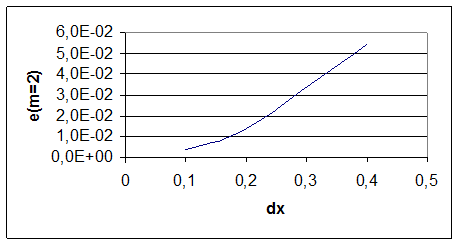
Рис. 6. График ошибки вычисления функции для m=2

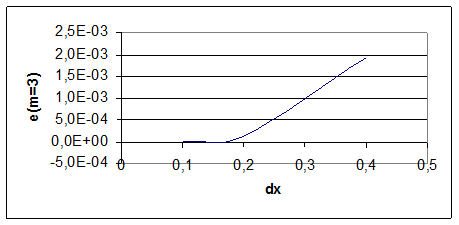
Рис. 7. График ошибки вычисления функции для m=3

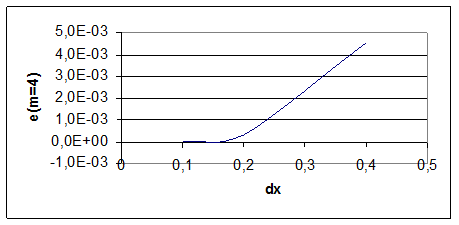
Рис. 8. График ошибки вычисления функции для m=4

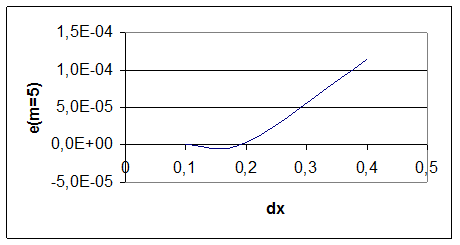
Рис. 9. График ошибки вычисления функции для m=5


7. Вывод

Исходя из экспериментальных данных, установили, что методическая погрешность убывает с увеличением m, но увеличивается с ростом dx, вычислительная погрешность возрастает.

Скачать файл